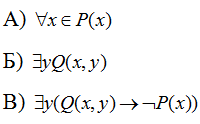Контрольная работа с курса Дискретная математика - 7 задач

Задание 1. Построить таблицы истинности следующих формул:

Задание 2. Формула 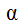 тождественно истинна всегда, когда истинна формула β. Будет ли формула α→β тождественно истинной?

Задание 3. Привести пример формул α и β таких, чтобы формула ⌐α˅⌐β→α была тавтологией.

Задание 4. Доказать схему вывода:

Задание 5. Пусть универсумом является множество целых чисел Z и P(x,y,z) = [x-y=z] – трехместный предикат на этом универсуме. Запишите с помощью логической символики следующее утверждение: «для всех х,у существует z такое, что x-z=y».

Задание 6. Пусть х и у – пременные, определенные на множестве людей. Введем следующие обозначения: М(х) = [x- мужчина]; D(x) = [х – женщина]; К(х,у) = [х- ребенок у]. Запишите в логической символике следующие предложения: «х и у – братья».

Задание 7. Пусть Р(х) – одноместный предикат, а Q(х, у) – двуместный предикат на множестве М={0,1,2,3,4}, заданные таблицей

Р: Q:

Составьте полные таблицы истинности для следующих формул: