Курсова робота Розробка алгоритму та програми для обчислення послідовності n! перестановок на множині {1,2,….,n}

Вступ

Розділ 1. Постановка завдання: розробка алгоритму та програми для обчислення послідовності n! Перестановок на множині {1,2,….,n}

Розділ 2. Математична постановка задачі

Розділ 3. Характеристика системи програмування Microsoft Visual C++2012

Розділ 4. Опис головної програми SawDM.exe

Розділ 5. Опис та обгрутування тестових прикладів виконаної програми SawDM.exe

Розділ 6. Тестування програми SawDM.exe

Розділ 7. Аналіз результату

Висновок

Список літератури

Основні теоретичні відомості:

Дискретна математика - це розділ математики, що вивчає дискретні фігури і їх структури. Дискретність - це окремі частини фігури ( дробова фігура). У цій категорії ви знайдете корисну інформацію про теорію множин, їх визначення і закони.

Теорія множин. В основі теорії множин лежать первинні поняття: множина та елемент множини. Елемент множини перебуває щодо множини у відношенні бути елементом множини (позначається як  — «x є елемент множини A»). Серед похідних понять найважливішими є наступні:

- порожня множина — множина, яка не містить елементів, позначається зазвичай ;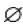

- підмножина і надмножина — множина, яка складається тільки з елементів іншої множини, та множина, до якої належать усі елементи іншої множини, відповідно;

- сімейство множин;

- простір (універсум) — множина, що є надмножиною всіх множин;

- конституента.

Над множинами визначені наступні операції:

- об'єднання (або сума) (позначається як );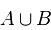

- перетин (або добуток) (позначається як );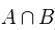

- різниця (позначається як рідше );

- симетрична різниця (позначається як 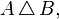рідше ).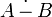

- доповнення (позначається як 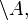або );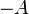

Для множин визначені наступні бінарні відношення:

- відношення рівності (позначається як );

- відношення включення (позначається як 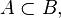або ).

Комбінаторика (Комбінаторний аналіз) — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай скінченної, множини відповідно до заданих правил. Кожне таке правило визначає спосіб побудови деякої конструкції із елементів вихідної множини, що зветься комбінаторною конфігурацією.

Тому на меті комбінаторного аналізу стоїть дослідження комбінаторних конфігурацій, алгоритмів їх побудови, оптимізація таких алгоритмів, а також розв'язання задач переліку. Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, комбінація та розбиття.

Комбінаторика пов'язана з багатьма іншими розділами математики. Термін «комбінаторика» ввів Лейбніц, який у 1666 році опублікував свою працю «Міркування про комбінаторне мистецтво». Іноді під комбінаторикою розуміють більш широкий розділ дискретної математики, що включає теорію графів.

Алгоритм не є складним для описання на програмному рівні так і на рівні розуміння його застосування.

1. Андерсон Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — С. 960. — ISBN 0-13-086998-8.

2. Белоусов А. И., Ткачев С. Б. Дискретная математика. Серия: Математика в техническом университете. Изд-во: МГТУ им. Н. Э. Баумана, 2001.- 744 с. ISBN 5-7038-1769-2, 5-7038-1270-4.

3. Виленкин Н. Я. Комбинаторика. — М., 1969.

4. Ерусалимский Я. М. Дискретная математика. — М., 2000.

5. Иванов Б. Н. Дискретная математика. Алгоритмы и программы. Издательство: Физматлит, 2007. — 408 с. ISBN 978-5-9221-0787-7.

6. Капитонова Ю. В., Кривой С. Л., Летичевский А. А., Луцкий Г. М. Лекции по дискретной математике. — СПб.: БХВ-Петербург, 2004. — С. 624. — ISBN 5-94157-546-7.

7. Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику. — М., 1963. — С. 486.

8. МЭС (1995), — М., БРЭ.

9. Новиков Ф. А. Дискретная математика для программистов. — 2-е изд. — СПб.: «Питер», 2005. — С. 364. — ISBN 5-94723-741-5.

10. Редькин Н. П. Дискретная математика. Издательство: Лань, 2006. — 96 с. ISBN 5-8114-0522-7

11. Романовский И. В. Дискретный анализ. — 4-е изд. — СПб.: Невский Диалект; БХВ-Петербург, 2008. — С. 336.

12. Яблонский С. В. Введение в дискретную математику. — М.: Наука, 1979. — С. 272.

13. Глинський Я. М. С++ і С++ Builder / Я. М. Глинський, В. Є. Анохін, В. А. Ряжська – Львів: Деол, 2003 - 193 с.