Лабораторна робота №5, Двошаровий персептрон

« Назад

Мета: набути досвід застосування багатошарових персептронів при моделюванні найпростіших логічних функцій.

Хід роботи

1. Ознайомитися та вивчити теоретичний матеріал.

Теоретичний матеріал

Обмеженість одношарового персептрона. Як вже зазначалося вище, Ф. Розенблатту вдалося навчити свій персептрон розпізнавати букви алфавіту. Це був колосальний успіх: електронний пристрій, створений за образом і подобою людського мозку, навчений подібно до людини, успішно моделював інтелектуальні функції людини. Це був успіх в пізнанні самої природи людського мислення. Мозок почав розкривати свої таємниці. З’явилася можливість досліджувати мозок методами моделювання, не вдаючись до складних антигуманних і мало що даючим експериментам. Це була сенсація, що прикувала до себе увагу мислячих людей усього світу. Здавалося, що ключ до інтелекту був знайдений і повне відтворення людського мозку і всіх його функцій – всього лише питання часу. Письменникам-фантастам, вченим інженерам, бізнесменам, політикам бачилися дуже райдужні перспективи практичного застосування ідей штучного інтелекту. Уряд Сполучених Штатів Америки виділив великі субсидії на розвиток нового перспективного наукового напряму.

Клас розв’язуваних нейромережами задач розширювався. Але в міру розширення фронту наукових досліджень з’явилися труднощі. Несподівано виявилося, що багато нових завдань персептрон вирішити не міг. Причому ці нові завдання, зовні нічим не відрізнялися від тих, з якими персептрон успішно справлявся раніше. Виникла необхідність пояснення парадоксів, глибокого аналізу та створення теоретичної бази нейроінформатики.

Наступний період історії штучного інтелекту розпочався з появи в 1969 р. книги двох відомих американських математиків М.Мінського і С.Пайпера «Персептрони». Автори цієї книги математично довели, що одношарові персептрони, що використовувалися в той час, в принципі не здатні вирішувати багато простих завдань. Одну з таких задач, що увійшла в історію нейроінформатики під назвою проблеми «Исключающего ИЛИ», ми розглянемо докладно.

«Исключающее ИЛИ» - це логічна функція двох аргументів, кожен з яких може мати значення «істинно» або «хибно». Сама вона приймає значення «істинно», коли тільки один з аргументів має значення «істинно». У всіх інших випадках ця функція приймає значення «хибно». Якщо закодувати значення «істинно» одиницею, а значення «хибно» - нулем, то потрібну відповідність між аргументами х₁, х₂ і самої функції у можна представити у вигляді табл. 1, так званої таблиці істинності логічної функції.

Таблиця 1

Таблиця істинності логічної функції «Исключающее ИЛИ»

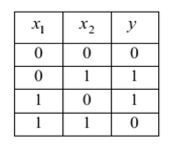
Завдання полягає в тому, щоб навчитися моделювати функцію «Исключающее ИЛИ» за допомогою однонейронного персептрона з двома входами х₁, х₂ і одним виходом у (рис. 1). При виконанні лабораторної роботи №1 Ви вже намагалися вирішити цю задачу шляхом підбору значень синаптичних w₁, w₂ і порога θ, проте зробити це Вам не вдалося. Вам не вдалося це зробити, хоча в інших випадках, при моделюванні логічних функцій «И» і «ИЛИ», у Вас проблем не виникало.

Зовні функції «И». «ИЛИ» та «Исключающее ИЛИ» мало чим відрізняються один від одного, і Вам було не зрозуміло, чому Ваш однонейронний персептрон успішно справлявся з моделюванням двох перших функцій, а з моделюванням третьої функції він впоратися не міг.

Рис. 1 - Однонейронний персептрон з двома входами і одним виходом

Для пояснення цього парадоксу американськими математиками М.Мінським і С.Пайперт була запропонована геометрична інтерпретація, яка полягає у наступному. Вони запропонували зобразити на координатній площині х₁ і х₂ всі можливі комбінації вхідних сигналів у вигляді чотирьох точок: А, В, С, D, як показано на рис. 2. Точка А має координати х₁=0, х₂=0; точка В має координати х₁=0, х₂=1 і т.д. згідно табл. 2.

Таблиця 2

Таблиця істинності логічної функції «Исключающее ИЛИ», доповнена точками А, В, С, D

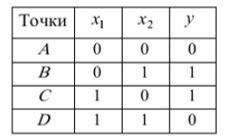
Тоді в точці А вихід персептрона у має дорівнювати нулю, в точці В – одиниці, в точці С – одиниці і в точці D – нулю.

Рис. 2 - Графічна інтерпретація до пояснення проблеми Исключающего ИЛИ

Як нам відомо (див. наприклад лабораторну роботу №1), математичний нейрон Мак-Каллока – Піттса, зображений на рис. 1, здійснює

 

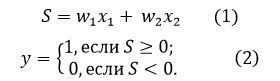
перетворення.

Замінимо в рівняння (1)  на θ:

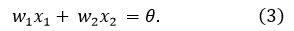
Якщо В цьому рівнянні величини х₁ і х₂ вважати змінними, а θ, w₁, w₂ - константами, то на координатній площині х і х₂ рівняння, шо розглядається зобразиться у вигляді прямої лінії, положення і нахил якої визначаються значеннями коефіцієнтів w₁, w₂ і порога θ. Для всіх точок площині х₁ і х₂, шо лежать на цій лінії, виконується рівність S = θ і тому, відповідно до формули (2). вихід персептрона дорівнює одиниці.

Для точок, шо лежать вище вказаної лінії сума більша ніж  θ, і тому за формулами (1) - (2) вихід персептрона також дорівнює одиниці, а для точок, шо лежать нижче цієї лінії, сума  менша ніж θ, і вихід персептрона дорівнює нулю. Тому лінію, яка зображує рівняння (3). називають пороговою прямою.

А тепер подивимося на табл. 2. Згідно з цією таблицею в точках А і D вихід персептрона повинен бути нульовим, а в точках В і С - одиничним. Але для цього треба розташувати порогову пряму так, щоб точки А і D лежали нижче цієї лінії, а точки В і С - вище, шо неможливо. Це значить, шо, скільки б персептрон не навчали, які б значення не надавали його синаптичним вагам і порогу, персептрон в принципі не здатний відтворити співвідношення між входами і виходом, шо потребує таблиця істинності функції «Исключающее ИЛИ».

Крім проблеми «Исключающего ИЛИ» М. Мінський і С. Пайперт привели ряд інших завдань, в яких точки, шо зображують вхідні сигнали, не можуть бути розділені пороговою прямою (в багатовимірних випадках - площиною, гіперплощиною). Такі завдання отримали назву лінійно нероздільних.

Після виходу в світ книги М. Мінського і С. Пайперт «Персептрони» всім стало ясно, шо активно вживали в той час спроби навчати персептрони вирішенню багатьох завдань, які. як виявилося, відносяться до класу лінійно нероздільних, з самого початку були приречені на провал. Це була порожня трата часу, сил і фінансових ресурсів.

Однонейронний персептрон в принципі не дозволяє моделювати логічну функцію «Исключающее ИЛИ» і вирішувати інші лінійно нероздільні завдання.

Рішення проблеми «Исключающего ИЛИ». Поява книги М. Мінського і С. Пайперта «Персептрони» викликала шок в науковому світі. Суворі математичні докази М. Минского і С. Пайперта були невразливі. Загальний ентузіазм змінився не менш загальним песимізмом. В газетах стали з'являтися критичні статті з повідомленнями про те. шо вчені мужі у своїх дослідженнях зайшли в тупик, даремно витративши величезні державні гроші. Уряд С'ША негайно припинив фінансування нейропроектів і приступив до пошуків винних. Бізнесмени, шо втратили надію повернути вкладені капітали, відвернулися від вчених і нейроінформатика була віддана забуттю, яке тривало понад 20 років.

Проте, роботи в області нейромережевих і нейрокомп'ютерних технологій тривали окремими ентузіастами. Роботи тривали в засекречених науково-дослідних інститутах Радянського Союзу, відокремленого в той час від Заходу «залізною завісою». Не маючи інформації про настрої зарубіжних колег, радянські вчені спокійно продовжували займатися цією темою і до початку 80-х рр. здивували світ ракетами та літаками, шо керувалися комп'ютерами нового покоління - нейрокомп'ютерами. Радянські комп’ютери, на відміну від американських, стійко переносили досить серйозні пошкодження, продовжуючи працювати в складних умовах, шо було особливо важливо для об'єктів військового призначення. Виявилася ще одна властивість нейрокомп’ютерів. успадкована від мозку - властивість живучості.

Радянським ученим С. О. Мкртчаном було показано, шо за допомогою багатошарових персептронів може бути змодельована будь-яка логічна функція, якщо тільки відома її логічна формула. Більш того, ним був розроблений спеціальний математичний апарат, шо дозволяє конструювати такі персептрони. Виявилося, шо проблема «Исключающего ИЛИ», шо стала каменем спотикання для однонейронного персептрона. може бути вирішена за допомогою нейронної мережі, шо складається з трьох нейронів - тринейронного персептрона. зображеного на рис. 3.

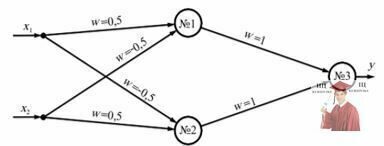
Рис. 3 - Нейронна мережа, що моделює функцію Исключающее ИЛИ

Робота цього персептрона відбувається за наступним алгоритмом.

Нейрон №1:

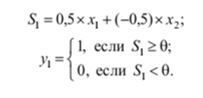
Нейрон №2:

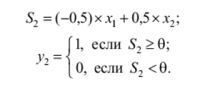
Нейрон №3:

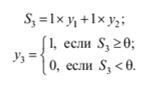
Задавшись значенням порога θ = 0,5 і заповнивши за допомогою цих формул табл. 3, легко переконатися, що три нейронний персептрон успішно моделює функцію «Исключающее ИЛИ».

Таблиця 3

Процес формування сигналів в тринейронному персептроні

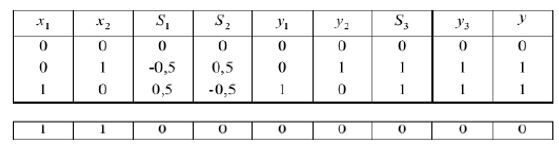
Згодом було показано, шо й інші лінійно нероздільні завдання, наведені в книзі М. Мінського і С\ Пайперта. можуть бути вирішені за допомогою нейромереж, шо містять один або кілька прихованих нейронних шарів, тобто шарів нейронів, розташованих між вхідним і вихідним шарами.

Багато дослідників розуміти, шо потрібно створювати нейромережі більш складної архітектури, шо містять приховані шари нейронів, але не уявляли, як такі мережі навчати. Правила Хебба та їх узагальнення - дельта-правило. годилися тільки для коригування синаптичних ваг нейронів вихідного шару, тоді як питання про налаштування параметрів прихованих нейронних шарів залишалося відкритим.

Логічну функцію «Исключающее ИЛИ» може моделювати нейронна мережа, шо складається з трьох нейронів, зображена на рис. 3.

Алгоритм зворотного поширення помилки. Ефективний алгоритм навчання багатошарових персептронів, що відкрив шлях їх широкого практичного застосування, став відомий тільки в 1986 р. завдяки публікаціям Д. Румельхарта. Г. Хілтона і Р. Вільямса. Ідея цього алгоритму полягає в тому, шо помилки нейронів вихідного шару ε_і = d_i = y_i використовуються для обчислення помилок нейронів, розташованих в прихованих шарах. Значення помилок як би поширюються від вихідного шару нейронів всередину мережі від подальших нейронних шарів до попередніх. Звідси назва методу алгоритмом зворотного поширення помітки (back propagation).

Цікаво відзначити, що алгоритм зворотного поширення помилки був запропонований на один рік раніше в роботах А. Паркера і А. Ле-Кана. вішаних незалежно одна від іншої. Більш того, oе в 1974 р. цей простий і витончений алгоритм був захищений П. Вербосом в його докторській дисертації. Однак тоді він залишився непоміченим, і тільки через десять років був «перевідкритий» заново і отримав загальне визнання та застосування. Залишилися непоміченими і роботи радянських вчених, які ще раніше розробляли подібні алгоритми у своїх засекречених інститутах і успішно застосовували їх при побудові систем управління об'єктами військового призначення.

Розглянемо ідею алгоритму зворотного поширення помилки, спробувавши узагальнити дельта-правило на випадок навчання двошарового персептрона. що має N входів, І виходів і прихований шар з J нейронів (рис. 4). Цей персептрон насправді має три шари, однак в літературі його називають двошаровим, оскільки нейрони вхідного шару мають всього один вхід, не мають синаптичних ваг і не виконують підсумовування вхідних сигналів, а лише передають один єдиний вхідний сигнал нейронам наступного шару.

Алгоритм коригування синаптичних ваг нейронів вихідного шару залишимо таким же. як для одношарового персептрона (див. узагальнене дельта-правило: теоретичний матеріал до лабораторної роботи № 4). замінивши x_j на y_j:

Рис. 4 - Двошаровий персептрон з N входами, І виходами і прихованим шаром з J нейронів

Синаптичні ваги нейронів прихованого шару спробуємо коригувати за допомогою тих же формул, в яких індекс і замінимо на j, а індекс j замінимо на індекс n:

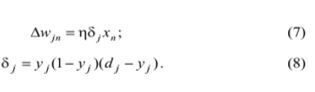
При використанні цих формул виникає питання про обчислення нейронної помилки (d_j -  y_j), яка для прихованого шару невідома. Ідея авторів розглянутого алгоритму полягала втому, щоб в якості цієї помилки використовувати сумарні нейронні помилки з вихідного шару, помножені на сили відповідних синаптичних зв’язків, тобто

Отже, для прихованого шару остаточно маємо

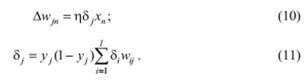
Використовуючи цю ідею, нескладно розписати алгоритм зворотного поширення помилки персептрона, що має довільну кількість прихованих шарів. Однак перш відзначимо, що ми будемо використовувати нейрони, що мають сигмоїдну функцію (див. теоретичний матеріал до лабораторної роботи №4), і виконують операцію підсумовування з урахуванням нейронного зміщення (див. теоретичний матеріал до лабораторної роботи №1):

Тут w_i0 – вага додаткового входу і-го нейрона, що імітує його заміщення b₁, а х₀ = 1 – величина сигналу додаткового входу.

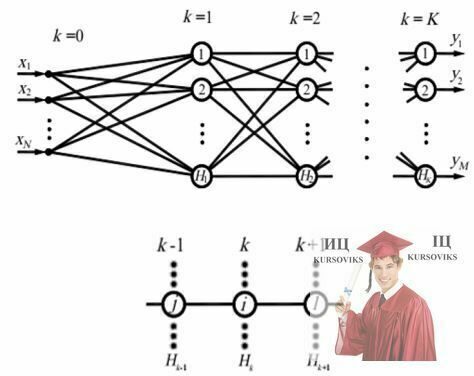
Рис. 5 - Багатошаровий персептрон (MLP – MultiLayerPerseptron)

Алгоритм зворотного поширення помилки розпишемо для багатошарового персептрона. шо має вхідний шар k= 0. кілька прихованих шарів k= 1.2, .... К-1 та вихідний шар k = К (рис. 5).

Нейрони вхідного шару не виконують математичних перетворень, а лише передають вхідні сигнали нейронам першого шару. Будемо вважати, шо кожен k-й шар містить Н_k нейронів. Таким чином, персептрон має N =Н₀ входів і М = Н_k виходів. В алгоритмі будемо використовувати наступні позначення: і - порядковий номер нейрона k-то шару: j - порядковий номер нейрона (k - 1)-го шару: l - порядковий номер нейрона (k + 1)-го шару (рис. 5, внизу).

Крок 1. Ініціалізація синаптичних ваг і зміщень.

В циклах по k= 1.2, .... К; і = 1, 2, …, Н_k;   j = 0, 1, 2, …., Н_k-1 синаптичним вагам і зсувам 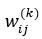 датчиком випадкових чисел присвоюються малі величини, наприклад, з інтервалу від -1 до +1.

Крок 2. Відкриття циклу по q =1. 2, .... Q. Подання з навчальної множини прикладів чергового вхідного вектора Х_q=(х₁, х₂, х_N)_q і відповідне йому бажаного вихідного вектора  D_q=(d₁, d₂, …, d_M)_q. де q - номер прикладу в навчальній множині.

Крок 3. Прямий прохід.

В циклах по по k= 1.2, .... К; і = 1, 2, …, Н_k;   обчислюються вихідні сигнали i-го нейрона в k-му шарі

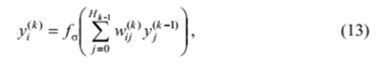
де 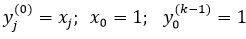; вихідні сигнали персептрона .

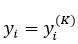Крок 4. Зворотній прохід.

В циклах по k= 1.2, .... К; і = 1, 2, …, Н_k;   j = 0, 1, 2, …., Н_k-1 обчислюються синаптичні ваги в новій епосі

де

причому для вихідного шару k=K згідно (8)

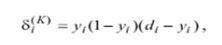
а для всіх інших прихованих шарів згідно (11)

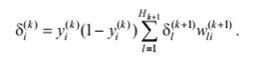
Крок 5. Закриття циклу по q.

Крок 6. Повторення кроків 2 - 5 необхідну кількість разів.

Вектори навчальних прикладів Х_ч і D_q на кроці 2 алгоритму звичайно представляються послідовно від першого до останнього, тобто q = l, 2, …,Q,     де Q - загальна кількість прикладів. Наприклад, у разі розпізнавання букв алфавіт}' 0= 33. Після того, як для кожного навчального прикладу будуть скориговані вагові коефіцієнти персептрона. тобто кроки 2-4 будуть повторені 33 рази, на кроці 6 алгоритму обчислюється середньоквадратична помилка, усереднена по всіх навчальних прикладам:

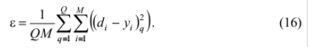
Крім середньоквадратичної помилки може бути також оцінена максимальна різниця між бажаними і прогнозованими (те. шо обчислив персептрон) виходами персептрона:

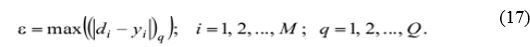
Ітераційний процес, шо задається кроком 6. закінчується після того, як помилка є. шо обчислюється за формулами (16) або (17). досягне заданої величини, або коли буде досягнута гранична кількість епох навчання. В результаті персептрон навчиться виконувати потрібне відображення будь-якого вхідного вектора Х_q на вихідний вектор Y_q, шо відрізняється від бажаного вектора D_q на деяку малу величину.

Коротко про головне. Першим алгоритмом навчання нейронної мережі були правила Хебба. призначені для навчання одношарового персептрона з нейронами, шо мають ступінчасті активаційні функції. Потім було введено поняття нейронної помилки як різниці між необхідним виходом нейрона d_i і його реальним значенням у_i В результаті алгоритм навчання персептрона за допомогою правил Хебба був узагальнений у вигляді алгоритму дельта-правила. В ітераційних формулах алгоритму дельта-правила з'явився коефіцієнт швидкості навчання η, шо дозволяє впливати на величину ітераційного кроку.

Потім була запропонована сігмоїдна активаційна функція і було введено поняття квадратичної помилки навчання персептрона. В результаті з'явилося узагальнене дельта-правило, що реалізує метод градієнтного спуску і шо дозволяє працювати не тільки з бінарними, але і з безперервними сигналами. Алгоритм зворотного поширення помилки є наступним узагальненням узагальненого дельта-правила і дозволяє навчати не лише одношарові, а й багатошарові персептрони.

Види активаційних функцій. В сучасних нейронних мережах і нейропакетах найбільш часто застосовуються такі види активаційних функцій.

Порогові активаційні функції (функції-сходинки). Порогові активаційні функції-сходинки можуть мати як несиметричний (рис. 6 а), так і симетричний (рис. 6 б) відносно початку координат вид.

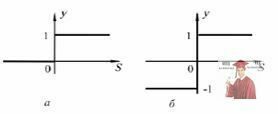
Рис. 6 - Порогові активаційні функції-сходинки

Їх аналітичне подання відповідно для рис. 6а та рис. 6б:

де 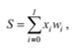причому х_о =1 - величина сигналу додаткового входу, а  - w₀ - його вага, шо імітує нейрони зміщення b (яке дорівнює порогу чутливості нейрона, взятому з протилежним знаком: b= - θ).

Ступінчасті активаційні функції зазвичай використовуються в задачах розпізнавання образів. Персептрони зі східчастими активаційними функціями можуть навчатися за допомогою правил Хебба і дельта-правила.

Узагальнене дельта-правило і алгоритм зворотного поширення помилки для навчання таких персептронів не годяться, так як в ці алгоритми включають знаходження похідних від активаційних функцій, шо неможливо для функцій, шо мають розрив.

Лінійні активаційні функції. На рис. 7а представлений графік лінійної активаційної функції у = S. Область зміни цієї функції необмежена.

Такі активаційні функції зазвичай застосовуються в нейронах вхідного

Такі активаційні функції зазвичай застосовуються в нейронах вхідного шару. Вони також непогано працюють при вирішенні простих лінійно розділених задач, причому з навчанням таких персептронів можуть справлятися алгоритми дельта-правила. узагальненого дельта-правнла і алгоритм зворотного поширення помилки.

Іноді застосовують лінійні активаційні функції з обмеженою областю зміни (рис. 7 6):

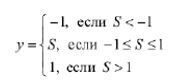
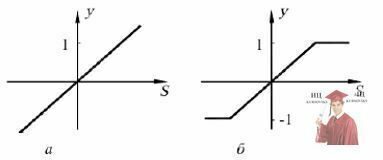
Рис. 7 - Лінійні активаційні функції з необмеженою (а) і обмеженою (б) областями зміни

Сигмоїдна активаційні функції. На рис. 8а зображений графік сигмоїдної функції, заданої рівнянням

 

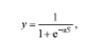
а на рис. 86 - графік функції, заданої рівнянням

 

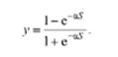
У цих рівняннях коефіцієнт а впливає на кут нахилу ліній до осі S. Аналогічний представленому на останньому графіку вигляд мають функції арктангенса 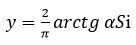 і гіперболічного тангенса 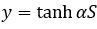, а також функція 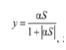які теж називають снгмоїдними.

Рис. 8 - Сигмоїдні активаційні функції з несиметричною (а) і симетричною (б) областями зміни

Персептрони з сигмоїдними активаційними функціями добре навчаються за допомогою алгоритму зворотного поширення помилки, а також за допомогою дельта-правила і узагальненого дельта-правила (якщо персептрон одношаровий).

Логарифмічні активаційні функції.На рис. 9 представлений графік активаційної функції, заданої рівнянням

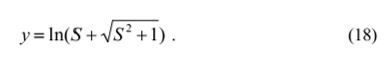
На відміну від сигмоїдної ця функція має необмежену область зміни. Іноді це зручно, так як не вимагається масштабування вихідних сигналів персептрона (докладніше про це див. теоретичний матеріал до лабораторної роботи №8). Крім того, логарифмічні активаційні функції дозволяють уникати небажаного ефекту, шо називається паралічем мережі - втратою чутливості мережі до варіацій вагових коефіцієнтів і. як наслідок, завмирання процесу навчання при попаданні зважених сум вхідних сигналів нейрона в область насичення сигмоїд (див. лабораторну роботу №8).

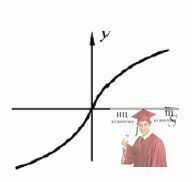
Рис. 9 - Логарифмічна активаційна функція

Радіально-базисні активаційні функції.Останнім часом набувають поширення нейромережі. нейрони яких мають активаційні функції у формі функції Гаусса (див. рис. 10):

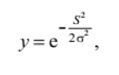
де S =||X – C|| - евклідова відстань між вхідним вектором X і центром активаційної функції С: 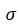 - параметр кривої Гаусса. шо називається шириною вікна. Такі активаційні функції називають радіально-базисними (RBF), а відповідні нейронні мережі - RBF-мережами.

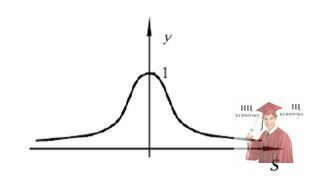
Рис. 10 - Радіально-базисна активаційна функція

Відзначимо, шо всі наведені вище активаційні функції, за винятком порогової і кусочно-лінійної, є безперервно диференційованими. Лінійна функція та логарифмічна функція виконують перетворення нескінченного вхідної множини значень змінних S в нескінченну множину змінних у. Порогові активаційні функції перетворюють множину значень S в бінарні множини: у=0 і у=1 або у= -1 і у=1. Решту активаційні функції перетворять нескінченну вхідну множину значень S в обмежені вихідні множини: у є (0,1), у є (-1, 1) і у є (0, 1). Від використовуваних активаційних функцій залежать функціональні можливості нейронних мереж, а також вибір способів їх навчання.

Активаційні функції здійснюють перетворення зваженої суми вхідних сигналів нейрона в його вихідний сигнал. Від виду активаційних функцій залежать функціональні можливості нейронних мереж, а також вибір способів їх навчання.

2. Завантажити файл LRl.exe. Виконати лабораторну роботу № 1 з розумінням геометричних малюнків у правій нижній частині вікна: «График выхода нейрона».

3. Завантажити файл LR5.exe.

4. Підібрати по два вдалих набори параметрів персептрона для кожної змодельованої функції:         «И», «ИЛИ», «Исключающее ИЛИ». Перевірити, чи вийде рішення задачі у випадку використання лінійної функції активації (відповідь має бути негативною), функції-сходинки (відповідь позитивна) і сигмоїди (відповідь позитивна), а також у разі застосування одношарового персептрона (відповідь негативна). Дослідити вплив коефіцієнта швидкості навчання на збіжність процесу навчання. Для кожної функції активації (сходинки, сигмоїди) отримати криві збіжності при різних коефіцієнтах η, кожну таку криву скопіювати (шляхом натискання клавіші Page Dawn) і підготувати звіт, виявивши за допомогою цих кривих найкраще для даного завдання значення коефіцієнта швидкості навчання η.

5. Чому один і той же персептрон при повторних запусках дає різні результати: процес навчання за одну і ту ж кількість епох в деяких випадках призводить до вирішення завдання, а в деяких випадках - ні?

6. Зробити покроковий звіт з обов'язковими скрінами і висновками.

7. Вислати на ел. почту файл.