Лабораторна робота №4, Розпізнавання рукописних літер

« Назад

Мета: сформувати навчальні приклади і навчити персептрон розпізнавати рукописні літери.

Хід роботи

1. Ознайомитися та вивчити теоретичний матеріал.

Теоретичний матеріал

На рис. 1 представлена схема персептрона, призначеного для розпізнавання літер алфавіту. Персептрон має 33 вихідних нейрона: кожній літері алфавіту відповідає свій вихідний нейрон. Сигнал першого вихідного нейрона у₁ має дорівнювати одиниці, якщо персептрону пред’явлена літера «А», і нулю для всіх інших літер. Вихід другого нейрона буде дорівнювати одиниці, якщо персептрону пред’явлена літера «Б», і нулю у всіх інших випадках. І так далі до букви «Я».

Рис. 1 - Персептрон, що призначений для розпізнавання літер алфавіту

При виконанні попередньої лабораторної роботи ми переконалися що персептрон навчився розпізнавати не тільки літери, на яких його навчали, а й літери, яких в навчальній множні не було, якщо вони не дуже відрізнялися від літер навчальної множини. Властивість розпізнавати нові образи, які персептрон ніколи «не бачив», ми назвали властивістю узагальнення.

Подальший розвиток ідеї персептрона був пов'язаний зі спробами розширити коло його застосування та удосконалити алгоритм навчання. Істотний розвиток персептрона було зроблено американськими вченими Б. Уідроу і М.Е. Хоффом, які замість вивченої на першій лабораторній роботі ступінчастою активаційної функції ввели безперервну нелінійну функцію активації

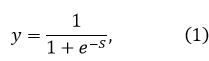
графік якої зображений на рис. 2.

Цю функцію назвали сигмоїдою, через те, що її графічне зображення нагадує латинську букву «S». Інша назва сигмоїди – логістична функція.

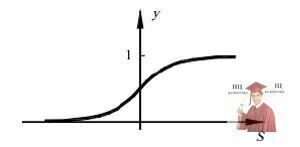
Рис. 2 - Сигмоїдна активаційна функція y = f₀(S)

Подібно звичайній пороговій функції активації, сигмоїда відображає точки області визначення 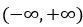 в значення з інтервалу (0, +1). Практично сигмоїда забезпечує безперервну апроксимацію класичної порогової функції.

Для сигмоїда взяли позначення y = f₀(S). Персептрони з сигмоїдними активаційними функціями з одним виходом назвали Адаайн, з кількома виходами – мадалайн (від англійських слів ADAptve LInear NEuron та Many ADALINE).

Поява персептронів з безперервними активаційними функціями зумовило появу нових підходів до їх навчання. Б. Уідроу і М.Е. Хофф запропонували мінімізувати квадратичну помилку, котру визначаємо формулою:

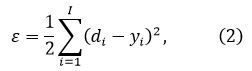
в якій  - необхідний (бажаний) вихід і-го нейрона, а  - той, який вийшов в результаті обчислень персептрона.

Розглянемо алгоритм корекції вагових коефіцієнтів персептронів, що має J входів і I виходів (рис. 3).

Рис. 3 - Персептрон з J входами і I виходами

Квадратична помилка навчання персептрона ε залежить від того, якими є вагові коефіцієнти w_ij. Іншими словами ε є функцією від вагових коефіцієнтів w_ij: ε = ε(w_ij). У шкільних курсах вивчаються функції тільки від одного аргументу у = у(х), які на координатній площині х, у зображуються у вигляді кривих ліній. Якщо функція z залежить від двох аргументів z = z (х, у), то вона зображується в тривимірній системі координат х, у, z у вигляді поверхні. Функція-помилка персептрона ε = ε(w_ij) залежить від великої кількості аргументів w_ij, тому для її графічного представлення вимагається багатовимірна система координат, яку ми в нашому тривимірному світі уявити собі не можемо. У цій багатовимірній системі координат ε = ε(w_ij) зображується у вигляді багатовимірної поверхні, яка називається гіперповерхністю.

Щоб хоч якось уявити собі гіперповерхність, припустимо, що всі аргументи w_ij мають постійні значення за винятком двох, наприклад w₁₂ і w₁₂, які є змінними. Тоді в тривимірній системі координат w₁₁, w₁₂, ε гіперповерхність матиме вигляд фігури, що нагадує параболоїд, яку назвемо псевдопараболоїдом (рис. 4). Процес навчання персептрона тепер можна представити як відшукання такого поєднання вагових коефіцієнтів w_ij, якому відповідає сама нижня точка гіперпсевдопараболоїда. Задачі подібного роду називається оптимізаційними. Кажуть, що оптимізаційна задача полягає в мінімізації функції ε = ε(w_ij) в багатовимірному просторі параметрів w_ij.

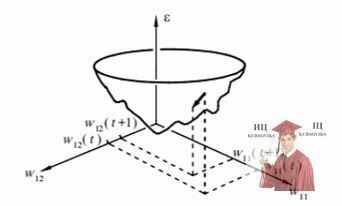
Рис. 4 - Графічне зображення функції-помилки персептрона ε = ε(w_ij) у тривимірній системі координат w₁₁, w₁₂, ε

Таким чином, якщо раніше говорили, що персептрон навчають методом «заохочення – покарання», то тепер стали говорити, що завдання навчання персептрона – це задача оптимізації (мінімізації) персептроном помилки (похибки).

Існує безліч методів вирішення оптимізаційних задач. Найбільш простим методом є перебір вагових коефіцієнтів w_ij з подальшими обчисленнями і порівняннями між собою відповідних цим коефіцієнтам значень функції ε. Більш ефективний метод градієнтного спуску, згідно з яким зміна (корекція) кожного вагового коефіцієнта Δw_ij виробляється в сторону, протилежну градієнту функції ε. Градієнт функції ε = ε(w_ij) являє собою вектор, проекціями якого на осі координат є похідні від функції ε по цих координатах (їх позначають 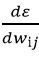), і що градієнт функції завжди спрямований у бік її найбільшого зростання. Оскільки наша задача полягає у знаходженні мінімуму функції ε = ε(w_ij), то нам треба опускатися по поверхні помилок, що забезпечується рухом у бік, протилежний градієнту цієї функції. Звідси і згадана вище назва – метод градієнтного спуску.

Рух у бік, протилежний градієнту (тобто протилежну напрямку зростання функції), здійснюватиметься, якщо на кожній ітерації до координат поточної точки w_ij ми будемо додавати величину, прямо пропорційну похідній координаті w_ij, взяту з протилежним знаком:

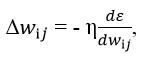, (3)

де η – деякий коефіцієнт, що задається в межах від 0,05 до 1, і називається коефіцієнтом швидкості навчання.

Зверніть увагу, що згідно з формулою (3) ми рухаємося не тільки в сторону зменшення функції, але і зі швидкості, прямо пропорційною швидкості убування (крутизні) функції, так як робимо крок Δw_ij, пропорційний похідній, взятої зі знаком мінус.

Квадратична помилка ε є складною функцією, яка залежить від вихідних сигналів персептрона у₁, які, в свою чергу, залежать від , тобто ε = ε(у₁(w_ij)). За правилом диференціювання складної функції

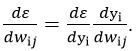. (4)

Вихідні сигнали нейронів у₁ обчислюється за допомогою сігмоїдних активаційних функцій у₁ = f₀(S₁), аргументом яких є суми

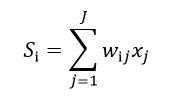
Отже,

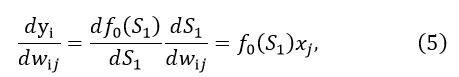
Крім того, якщо продиференціювати (2) по y_n, де n є [1, І], то вийде

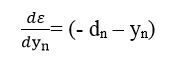
а значить

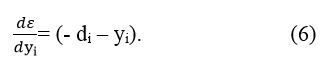
Підставивши (5) і (6) в (4), а потім отриманий вираз в (3), остаточно будемо мати

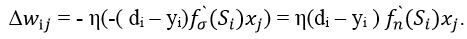 (7)

Цей вираз отримано для нейронів з активаційними функціями будь-якого виду. Якщо 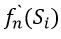 – сигмоїда, задана формулою (1), то

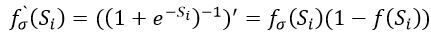.(8)

Підставивши цей вираз в (7), отримаємо:

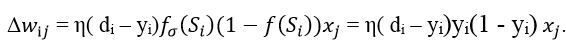. (9)

Отже, ми отримали ітераційну формулу для навчання персептрона

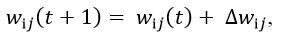, (10)

де

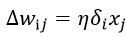, (11)

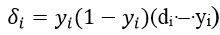 (12)

Введену ту за допомогою формули (12) величину 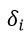 надалі будемо називати нейронною помилкою. Алгоритм (10)-(12) називають узагальненим дельта-правилом. Його перевага в порівнянні із звичайним дельта-правилом складається в більш швидкій збіжності і в можливості більш точної обробки вхідних і вихідних безперервних сигналів, тобто в розширенні кола розв’язуваних персептронами задач.

Отже, ведення сигмоїдної функції активації замість функції-сходинки і поява нового алгоритму навчання – узагальненого дельта-правила, розширило область застосування персептрона. Тепер він може оперувати не тільки з бінарними (типу «нуль» і «одиниця»), але і з безперервними (аналоговими) вихідними сигналами.

2. Завантажити файл LR4.exe.

3. Читаючи завдання, що з’являються в протоколі виконання в протоколі виконання намалювати на вхідному табто персептрона почергово букви (згідно варіанту, наприклад а, в, с) по три рази, кожен раз вказуючи мишкою на виході персептрона на ту букву, яка намальована. Намальовані букви плавно переміщаються в нижню частину екрану, де формують безліч навчальних прикладів. Після накопичення достатньої кількості прикладів з’являється кнопка «Обучить», при натисканні на яку запускається алгоритм навчання персептрона, що ілюструється графіком збіжності, тобто залежності помилки навчання від кількості епох навчання t.

4. Потім Вам пропонується за допомогою миші вибрати будь-який приклад з навчальної множини. Обрана буква плавно піднімається вгору і поміщається на вхідному полі персептрона, після чого Ви запускаєте процес розпізнавання букви шляхом натискання кнопки «Распознать образ».

5. Намалюйте на вхідному полі ті ж самі букви знову і перевірте, чи буде персептрон розпізнавати знову намальовані букви. Зробіть висновки.

6. Зробити покроковий звіт з обов’язковими скріпами і висновками.

7. Вислати на електронну пошту файл.

 

Варіанти