Лабораторна робота №2, Класифікація чисел

« Назад

Мета: сформувати навчальні приклади і навчити персептрон класифікувати числа на парні і непарні.

Хід роботи

1. Ознайомитися та вивчити теоретичний матеріал.

Теоретичний матеріал

Я к ми вже знайдемо з пройденого матеріалу, американські вчені У. Мак-Каллок і В. Піттс запропонували математичну модель нейрона мозку людини, назвавши її математичним нейроном. Так само як і біологічний нейрон  мозку, математичний нейрон має кілька входів і один вихід. Крім того, він може існувати в збудженому і не збудженому станах, причому перехід в збуджений стан залежить від величини сигналів, що надходять до нього і сил синаптичних зв’язків. Таким чином, математичний нейрон вельми правдоподібно імітує структуру і властивості свого прототипу – біологічного нейрона мозку. На цій підставі У.Мак-Каллок і В. Піттс висловили сміливе припущення, яке згодом лягло в основу сучасної нейроінформатики. Вони припустили, що якщо математичні нейрони пов’язати між собою провідниками електричного струму, що імітують нервові волокна, то такий штучний мозок буде здатний вирішувати інтелектуальні завдання, подібно до того, як це робить природний людський мозок.

Ідея Мак-Каллока – Піттса була втілена в життя в 1958 р. американським ученим Френком Розенблаттом, що також вважається засновником нейроінформатики. Спочатку він створив комп’ютерну програму для ІВМ-794, що емулює діяльність математичних нейронів. Це була перша нейронна мережа або скорочено – нейромережа. Вона була названа персептроном від англійського слова perception – усвідомлення.

Потім, через два роки, Ф. Розенблатт змонтував електронний пристрій, в якому функції математичних нейронів виконували окремі електросхеми, що працюють на електронних лампах. Ц був перший нейрокомп’ютер, який успішно вирішував надзвичайно складну інтелектуальну задачу – розпізнавав літери латинського алфавіту, зображені на картках, які підносилися до його зчитувального пристрою – електронного ока.

Розберемо принцип дії персептрона на прикладі більш просто задачі, ніж задача розпізнавання літер. На рис. 1 наведено один із найпростіших варіантів виконання персептрона, призначеного для класифікації чи лес на парні і непарні. Уявімо собі матрицю з 12 фотоелементів, розташованих у вигляді чотирьох горизонтальних рядів по три фотоелемента в кожному рядку. На матрицю фотоелементів накладається картка із зображенням цифри, наприклад «4», як зображено на рис. 1. Якщо на будь-який фотоелемент потрапляє фрагмент цифри, то цей фотоелемент виробляє сигнал у вигляді одиниці в іншому випадку – нуль. На рис. 1 перший фотоелемент видає сигнал х₁ = 0, другий фотоелемент – х₂ = 1 і т.д.

Відповідно до формул

 

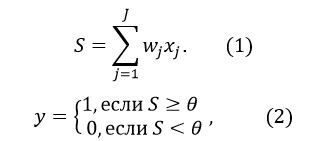
математичний нейрон виконує підсумовування вхідних сигналів x_j, помножених на синаптичні ваги w_j, після чого результат підсумовування S порівнюється з порогом чутливості θ і виробляється вихідний сигнал у.

початкові значення синаптичних ваг w_j і порога чутливості θ Ф. Розенблатт задавав датчиком випадкових чисел, тому на виході персептрона випадковим чином вироблявся сигнал: або 0, або 1.

Завдання полягало в наступному. Вимагалося підібрати значення синаптичних ваг w_j такими, щоб вихідний сигнал у приймав значення одиниця, якщо на картці було зображено парне число, і нуль, якщо число було непарним.

Рис. 1 - Персептрон, який класифікує числа на парні і непарні

Цю задачу Ф.Розенблатт вирішив шляхом почергового накладання на фотоелемент карток і навчання персептрона, що полягає у коригуванні синаптичних ваг w_j. Якщо, наприклад, на вхід персептрона пред’являлася картка з цифрою «4» і вхідний сигнал у випадково опинявся рівним одиниці, що означає парність, то коригувати синаптичні ваги було не потрібно. Так як реакція персептрона правильна. А якщо вихідний сигнал виявлявся рівним нулю, що неправильно, то слід було збільшити (заохотити) ваги тих активних входів, які сприяли збудженню нейрона. В даному випадку збільшенню підлягали w₂, w₁₁ та ін.

Дотримуючись цієї ідеї, можна сформулювати ітераційний алгоритм коригування синаптичних ваг, що забезпечує навчання персептрона в потрібному напрямку.

Крок 1. Датчиком випадкових чисел всім синаптичним вагам w_j (j=1,…,12) і порогу чутливості нейрона θ привласнити деякі малі випадкові значення.

Крок 2. Пред’явити персептрону яку-небудь цифру. Системою фотоелементів вироблюється вхідний вектор x_j (j=1,…,12).

Крок 3. Нейрон виконує зважене підсумовування вхідних сигналів

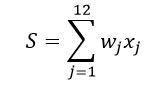
і виробляє вихідний сигнал у = 1, якщо S ≥ θ, або у = 0, якщо S ˂ θ.

Крок 4 а. Якщо вихідний сигнал правильний, то перейти на крок 2.

Крок 4 б. Якщо вихідний сигнал неправильний і дорівнює нулю, то збільшити ваги активних входів, додати кожній j-ій синаптичній вазі величину j-го вхідного сигналу:

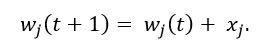
Тоді, якщо вхід був неактивним тобто x_j=0, то j-a синаптична вага не зміниться. Якщо ж він був активний, тобто x_j=1, то j-a синаптична вага буде збільшена на 1.

Тут і далі буква t означає номер ітерації, які в штучному інтелекті називаються епохами; w_j(t+1) - нове значення (на новому епосі) j-ї синаптичної ваги; w_j(t) - його старе значення (на попередньому епосі).

Крок 4 в. Якщо вихідний сигнал  неправильний і дорівнює одиниці, то зменшити ваги активних входів, наприклад за допомогою аналогічної формули:

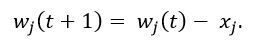
Крок 5. Перейти на крок 2 або завершити процес навчання.

У наведеному тут алгоритмі крок 4б називають першим правилом Хебба, а крок 4в – другим правилом Хебба на честь канадського вченого фізіолога Д.О. Хебба, який запропонував цей алгоритм в 1949 р. Відзначимо, що правила Хебба нагадують процес навчання дитини або школяра методом «заохочення - покарання» (або дресирування тварин методом «батога і пряника»). Як і у випадках з дитиною, яку навчають цим методом, алгоритм навчання персептрона за кінцеве число спроб (їх називають ітераціями або епохами) може призвести до мети – персептрон зрештою засвоїть необхідні знання, закодує їх у вигляді конкретних значень матриці сил синаптичних зв’язків  і, таким чином, навчиться розрізняти парні і непарні числа.

Природно виникає питання, чи завжди алгоритм навчання персептрона призводить до бажаного результату. Відповідь на це питання дає теорема збіжності персептрона:

Якщо існує безліч значень ваг, які забезпечують конкретне розрізнення образів, то в кінцевому підсумку алгоритм навчання персептрона приводить або до цієї множини, або до еквівалентної їй множині, такому, що дане розрізнення образів буде досягнуто.

В даний час вважається, що за числом виконаних доказів теорема збіжності персептрона займає перше місце в світі. Раніше самою доведеною в світі теоремою вважалася теорема Піфагора.

2. Завантажити файл LR2.exe.

3. Читаючи завдання, що з’являються в протоколі виконання за допомогою миші намалюйте на вхідному табло персептрона числа, а на виході персептрона вкажіть приналежність цих чисел до класу парних або непарних. Малювання виконується з натиснутою лівою кнопкою миші, а стирання намальованого – правою кнопкою. Кожна намальована цифра плавно спускається по екрану в нижню його частину, формуючи безліч навчальних прикладів (малювати цифри на весь зріст і не економити клітинки вхідного поля. Інакше можуть виникнути проблеми з навчанням персептрона). Хід виконання роботи протоколюється. Після того як накопичиться достатньо навчальних прикладів, з’являється кнопка «навчити», при натисканні на яку запускається алгоритм навчання персептрона, який ілюструється графіком збіжності. Спостерігаючи за побудовою цього графіка можна бачити, як помилка навчання персептрона ε убуває з кожною новою епохою t.

4. Зробити покроковий звіт з обов’язковими скріпами і висновками.

5. Вислати на електрону пошту файл.