Лабораторна робота №2, Дискретні моделі динамічних систем, Дослідження переходу системи до динамічного хаосу, Приклади моделей

« Назад

Мета: вивчення дискретних детермінованих моделей динамічних систем та дослідження їх поведінки.

Хід роботи

Теоретичні відомості

Исаак Ньютон сравнивал Вселенную с гигантским часовым механизмом, который создал бог и которому он дал первотолчок, не вмешиваясь далее в ход процессов.

Последователь Ньютона, выдающийся математик, механик, философ наполеоновской эпохи Пьер Симон Лаплас (1749–1827) развил этот взгляд. По его мысли, ум достаточно мощный, чтобы принять в расчет координаты и скорости всех частиц во Вселенной, мог бы заглянуть как угодно далеко и в будущее, и в прошлое. Такой взгляд, утверждающий полную предопределенность, получил название лапласовского детерминизма.

Таким образом, возникает фундаментальный вопрос: Возможен ли глобальный прогноз? Существует ли свобода воли? Лаплас настаивал на утвердительном ответе на первую половину этого вопроса. Но отсюда немедленно следует, что свободы воли нет, что все наши настоящие и будущие решения уже определены тем состоянием, в котором вселенная находилась в некоторый момент. Шекспир утверждал, что весь мир театр, а мы в нем все актеры. Лаплас идет дальше: мир в его понимании — кукольный театр, и мы всего лишь куклы в чужих руках и ничего не решаем.

Интересно, что именно Лаплас был основоположником теории вероятностей. Однако саму «вероятность» он считал лишь платой за наше незнание. Бросая монету в орлянке, можно было бы точно сказать, упадет ли она орлом или решкой, решая для нее уравнения механики. Но мы не знаем ее исходного положения и скорости, и поэтому вынуждены опираться на статистику. Следующая парадигма синергетики также связана с фундаментальной проблемой, которую почти три века относили к категории философских. Исаак Ньютон сравнивал Вселенную с гигантским часовым механизмом, который создал бог и которому он дал первотолчок, не вмешиваясь далее в ход процессов. В представлении, что все обстоит именно так, ученые прожили без малого 150 лет. Ситуацию изменила работа американского метеоролога Эдварда Лоренца (1917–2008) «О детерминированном непериодическом течении», появившаяся в 1963 году. Однако простейшая математическая модель, показавшая, что все может быть устроено именно так, как предполагал Э. Лоренц, появилась гораздо раньше. Эта модель была предложена Дж. Нейманом и Д. Уламом в качестве инструмента для получения случайных чисел (конечно, сейчас псевдослучайные числа получают с помощью компьютера совсем иначе и предъявляют к ним очень жесткие требования, но значение пионерских работ не стоит недооценивать).

Модель Дж. Неймана и Д. Улама получила название отображение «тент» (или «палатка»). Она определяет последовательность чисел по явной формуле:

Эту модель можно рассматривать как динамическую систему в случае дискретной временной переменной n =1,2,3... Состояние системы в момент n характеризуется числом x_n. Последовательность однозначно определяется начальным значением 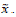Можно проверить, что если , то все элементы последовательности будут принадлежать интервалу [-1,1]. Если 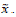 — иррациональное число из этого интервала, то и последовательность чисел не будет периодической.

Однако не эти любопытные свойства сделали модель «тент» классической, входящей во все учебники нелинейной динамики. Она позволяет проиллюстрировать удивительное свойство чувствительности к начальным данным. Рассмотрим две последовательности, которые генерирует обсуждаемое отображение  и 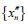. Для одной , а для другой , где величина ε очень мала. Тогда можно проверить, что

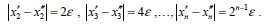
Другими словами, с каждым шагом расстояние между траекториями  увеличивается вдвое. И когда 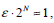, то, зная последовательность 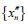, мы ничего не можем сказать о поведении . Представим теперь, что определяет динамику исследуемого объекта, а 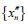 — описывающую его математическую модель. Тогда через

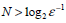− шагов мы теряем возможность следить за динамикой объекта, (эту величину, после которой нельзя дать прогноз состояния объекта, исследуя его модель, и ученые вынуждены опираться только на статистику, называют горизонтом прогноза).

Это означает, что взмах крыльев бабочки (изменившей начальное состояние атмосферы на очень малую величину ε ) может через некоторое время (для атмосферы горизонт прогноза — 2–3 недели) привести к разрушительному урагану за тысячи километров от нее. Важно взмахнуть в правильное время в правильном месте.

В чем же роль прикладной математики, к каковой можно отнести классическую работу Э. Лоренца? То, что простейшая динамическая система «тент», биллиарды с отрицательной кривизной границ и некоторые другие абстрактные модели могут иметь конечный горизонт прогноза, математикам было ясно еще в 1950-х годах.

Однако работа Лоренца, предложившего и изучившего простейшую модель конкретного физического явления — конвекции в подогреваемом снизу слое жидкости,

— стала началом научной революции. Проведенные компьютерные эксперименты показали, что эта ситуация типична. В простейшей нелинейной динамической с квадратичными нелинейностями наблюдается непериодическое движение (позже названное динамическим хаосом), а расстояние между двумя бесконечно близкими траекториями, как и в модели «тент», экспоненциально растет со временем

Величина λ, называемая ляпуновским показателем, является важнейшей характеристикой динамической системы и определяет горизонт прогноза

Исследователи привыкли к тому, что если достаточно долго подождать, то система выходит на некоторое притягивающее множество в фазовом пространстве — аттрактор и далее фазовые переменные выходят либо на постоянные значения (аттрактор — устойчивая особая точка), либо на периодический режим (аттрактор — предельный цикл). В случае модели Лоренца движение остается непериодическим, как бы долго мы его не наблюдали. Такие аттракторы, с легкой руки математиков Д. Рюэля и Ф.Такенса, были названы странными аттракторами.

После пионерской работы Лоренца странные аттракторы начали находить всюду — в радиотехнике и медицине, в экологии и экономике. Для солнечной активности и динамики магнитных полюсов Земли были предложены модели, описывающие динамический хаос. 

Завдання 1

Створити у своїй папці МЕД документ Ms Excel з ім’ям Лаб2_Прізвище.

Відкрити для роботи. Назвати робочий аркуш Модель «тент». Побудувати табличну модель у відповідності до різницевого рівняння

1) Провести дослідження впливу малого відхилення початкового значення моделі на поведінку системи і написати висновки, обґрунтувавши їх з позицій синергетики. Величина а₁ = 0,05* K. Величину відхилення обрати у відповідності до формули ε=0,001/K, де K – номер у списку журналу. Див. рис. 1.

Рис. 1 - Таблична модель тент

2) Перевірити виконання умови

Скласти таблицю відношення різниць до величини ε. Написати висновки.

2) Дослідити вплив початкових даних на траєкторію системи у фазовому просторі, написати висновки у табличній моделі.

Завдання 2

Дослідити перехід до динамічного хаосу детермінованої динамічної системи (логістичної моделі, яка ще має назву искретної моделі Ферхюльста)

 (2)

Створити новий робочий аркуш Д_Хаос. Змінюючи значення  і початкове значення х₁ побудувати траєкторію руху системи у фазовому просторі (спочатку створити табличну модель). Написати висновки.

1)  = 2 і x₁ = 0,1; 0,4; 0,8 (див. рис.2)

Рис. 2 - Наближення до стану рівноваги при різних початкових умовах (= 2)

2) Нехай тепер 3 <  < 3,449... Чисельний аналіз рівняння (2) при значенні = 3,2 (x₁ = 0,8) показує, що в системі встановлюються пе­ріо­дичні коливання з періодом 2 (рис. 3).

Рис. 3 - Періодичні коливання (= 3,2)

3) Нехай тепер 3 << 3,449... Чисельний аналіз рівняння (2) при значенні = 3,5 (x₁ = 0,8) показує, що в системі наявні пе­ріо­дичні коливання з періодом 4 (рис. 4).

Рис. 4 - Коливання з періодом 4 (= 3,5)

4) Послідовно збільшуючи параметр , ми побачимо цикли S⁸, S¹⁶, S³², S⁶⁴, S¹²⁸, S²⁵⁶ і т. д. При цьому кожен цикл S^2p втрачає стійкість і стійким стає цикл S^2p+1. Нарешті, при значенні  = 3,5699... (його іноді позначають ) формула (2) дає вже неперіодичну послідовність {x_n}. Поведінка виглядає випадковою. Неперіодичний, випадковий процес виникає як границя усе більш складних структур (циклів S^2p). Отже, хаос виникає як надскладна організація (цикл S^2оо) (рис. 5). Побудуйте відповідну табличну модель та траєкторію руху системи у фазовому просторі.

Рис. 5 - Аперіодичний рух (динамічний хаос) (= 3,9)

Зауваження

У 1971 р. американський вчений М. Фейгенбаум відкрив цікаву закономірність: послідовність  утво­рить зростаючу послідовність, яка швидко сходиться до точки накопичення  = 3,5699... Різниця значень , що відповідають двом послідовним біфуркаціям, зменшується щоразу з приблизно однаковим кое­фіцієнтом:

Знаменник прогресії 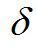   = 4,6692... нині називається постійною Фей­генбаума.

Незалежно від конкретного виду системи та її складності теорія універсальності Фейгенбаума дає кількісні передбачення. Константа 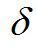 і ряд інших констант виступають як універсальні константи, такі ж, як  або е. Отже, ця теорія встановила, що великий клас нелінійних явищ демонструє не тільки однакову якісну поведінку, а й уні­вер­сальні кількісні закономірності.

Пізніше було виявлено ще кілька універсальних сценаріїв переходу до хаосу. Роботи останніх років дозволяють припустити, що в при­ро­ді, як правило, реалізовується всього кілька універсальних сценаріїв. Це величезний крок до розуміння внутрішньої єдності нелінійних явищ.