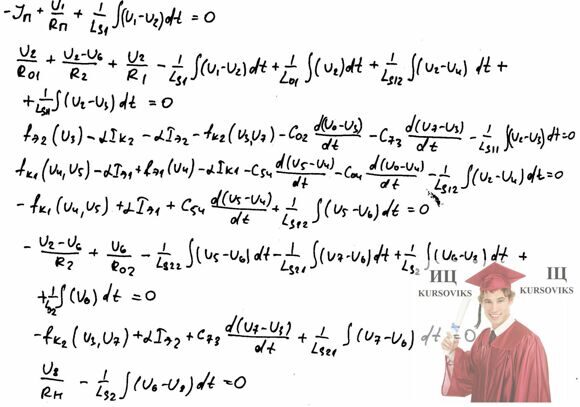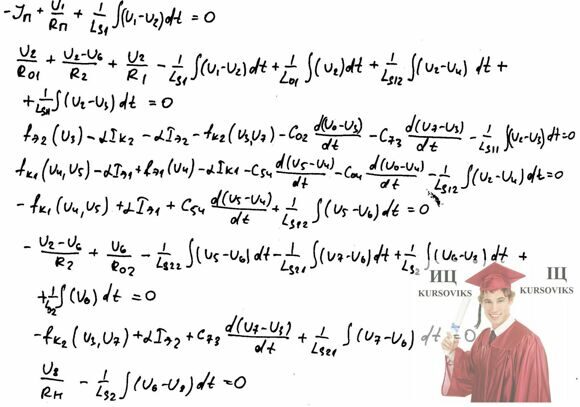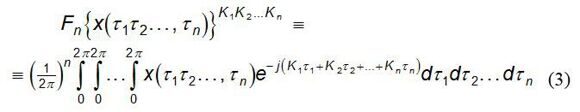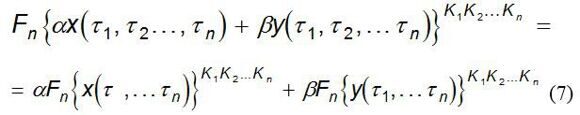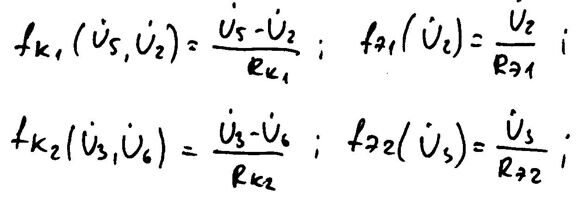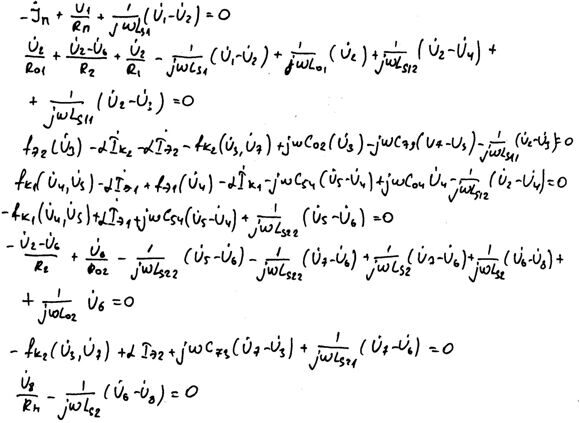Курсовая работа Разработка математических моделей схемы в различных режимах ее работы
Код роботи: 3073
Вид роботи: Курсова робота
Предмет: Теорія електричних кіл та сигналів (Теория электрических цепей и сигналов)
Тема: Разработка математических моделей схемы в различных режимах ее работы
Кількість сторінок: 40
Дата виконання: 2005
Мова написання: російська
Ціна: безкоштовно
Введение
1. Модель биполярного транзистора для различных режимов работы
2. Модель трансформатора в для различных режимов работы
3. Статический режим работы схемы
4. Алгоритм решения системы нелинейных уравнений методом Ньютона
5. Cхема при воздействии большого сигнала. Временная область
6. Алгоритм решения системы нелинейных уравнений методом Эйлера
7. Cхема при воздействии малого сигнала. Временная область
8. Cхема при воздействии большого сигнала. Частотная область
9. Cхема при воздействии двух гармонически не связанных больших сигналов. Частотная область
10. Cхема при воздействии малого сигнала. Частотная область
Приложение
ЗАДАНИЕ
на курсовой работе студента
1. Тема проекта: Разработка математических моделей схемы в различных режимах ее работы
2. Исходные данные:
2.1. Вариант электрической схемы №26
2.2. Указание по составлению математических моделей режимов работы схемы. Особенности формирования математических моделей, их применению и проверке формирования с использованием пакетов программ "МICROCAP-3", "МICROCAP-5"
3. Содержание расчетно-пояснительной записки:
3.1. Подробное описание формирования математических моделей схемы
3.2. Подробное описание алгоритмов решения задач анализа различных режимов работы схемы
3.3. Задания на расчет и результаты расчета анализа схемы во всех режимах ее работы с использованием пакетов программ "МICROCAP-3", "МICROCAP-5".
4. Перечень графического материала:
4.1. Электрическая схема, схема замещения, графы схемы для статического и динамических режимов
4.2. Структурные схемы алгоритмов решения задач анализа режимов работы схемы
4.3. Графические результаты выполнения п.4.4 настоящего задания.
Введение
Cхема варианта 10 задания
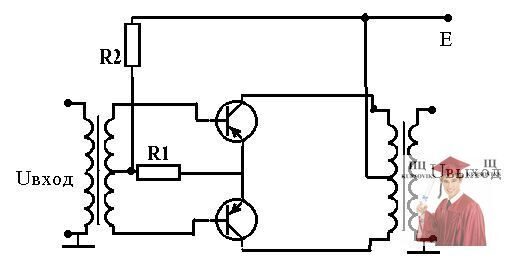
В тех случаях, когда однотактный каскад усиления мощности неприменим из-за указанных выше недостатков, а также когда мощность, отдаваемая одним транзистором, недостаточна, применяют двухтактную схему усиления мощности см рисунок В двух тактном каскаде используют два одинаковых транзистора, работающих в идентичных режимах. Каждый из транзисторов со своими цепями составляет плечо каскада.
Вторичная обмотка трансформатора предшествующего каскада имеет вывод от средней точки, Это необходимо для подачи на базы транзисторов двухтактного каскада двух равных по величине, но противоположных по фазе напряжений (Uвх1 и Uвх2.)
Выходной трансформатор имеет вывод от средней точки первичной обмотки. Резисторы R'Б и R''Б образуют делитель напряжения, обеспечивающий подачу требуемого напряжения смещения на базы транзисторов. Через средний вывод трансформатора Т2 подается напряжение на коллекторы транзисторов. Каждое плечо, взятое в отдельности, представляет собой обычный каскад усиления мощности с трансформаторным выходом, однако совместная работа двух плеч придает каскаду новые качества.
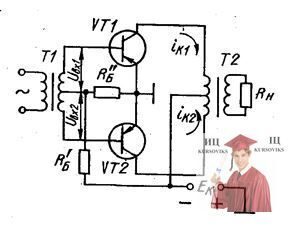
Рассмотрим процессы, происходящие в двухтактной схеме. Допустим, что входной сигнал на базах обоих транзисторов отсутствует и в коллекторных цепях транзисторов VT1 и VT2 проходят только постоянные составляющие токов Iк1p и Iк2p, величины которых определяются выбранным положением рабочей точки на характеристиках.
Как видно из рисунка, токи покоя протекают по первичной обмотке выходного трансформатора от средней точки в противоположных направлениях. Следовательно, при полной симметрия плеч магнитные поля, созданные этими токами, компенсируются, и в сердечнике трансформатора отсутствует постоянная составляющая магнитного потока (постоянное подмагничивание). Это является важным преимуществом двухтактной схемы перед одноактной, так как уменьшает нелинейные искажения в выходном трансформаторе (исключается возможность работы в области магнитного насыщения) и позволяет сделать его менее громоздким.
При подаче на базы транзисторов двух равных по величине в противоположных по фазе синусоидальных напряжений uвх1 и uвх2 результирующие напряжения на базах изменяются в противофазе.
Если, например, в данный момент на базу первого транзистора поступает отрицательное напряжение относительно эмиттера, а на базу второго — положительное, то:
iк1 = Iк1p + Iкм*sin(wt)
iк2 = Iк2p - Iкм*sin(wt)
Следовательно, переменные составляющие коллекторных токов транзисторов сдвинуты между собой по фазе на 180°.
Величина полезной мощности, отдаваемой в нагрузку, зависит от величины переменного магнитного потока в сердечнике выходного трансформатора, который пропорционален разности токов.
Таким образом, полезный магнитный поток пропорционален удвоённой переменной составляющей коллекторного тока и, следовательно, мощность в нагрузке равна сумме мощностей, развиваемых каждым транзистором.
1. Модель биполярного транзистора для различных режимов работы
Для описания математической модели используется модель биполярного транзистора Эберса-Молла.
Полная модель n-p-n биполярного транзистора имеет вид:
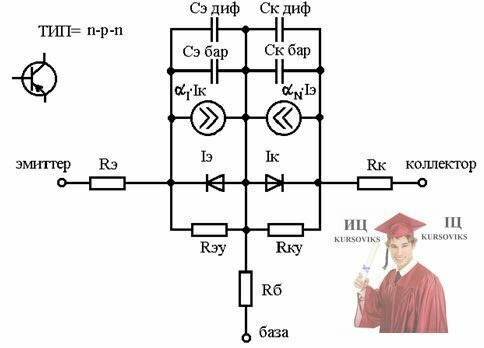
Сэ бар,Ск бар - барьерная емкость эмиттера и коллектора (моделирует емкость перехода p-n);
Сэ бар= Сэ бар0*(Uкэ бар- Uэ бар)-Nэ;
Ск бар= Ск бар0*(Uкк бар- Uк бар)-Nк;
Сэ бар0, Ск бар0, -коэффициенты пропорциональности;
Nэ, Nк - коэффициенты зависящие от распределения примеси в p-n переходе;
Сэ диф, Ск диф -диффузионная емкость эмиттера и коллектора (моделирует инерционность процесса распространения заряда в базе);
Сэ диф =Iэ/(mэ*jТ);
Ск диф =Iк/(mк*jТ);
Iэ, Iк -ток эмиттера и коллектора;
jТ- температурный потенциал;
mэ, mк- эмпирические коэффициенты;
aN*IЭ, aI*IK - ток генератора управляемого напряжением на соседнем переходе;
справедливо соотношение aN*IЭ=aI*IK=IО;
aN, aI - эмпирические функции напряжений на переходах;
IдЭ,IдК,- токи диодов (моделируют токи р-n переходов);
IдЭ= IнЭ*[exp(Uэб/(mэ*jТ))-1)];
IдК= IК*[exp(Uкб/(mк*jТ))-1)];
IнЭ, IнК- токи насыщения р-n переходов;
RЭУ, RКУ- сопротивления отражающие эффект Эрли.
Rэ, Rк, Rб - сопротивления эмиттера, коллектора и базы (моделируют наличие объемных сопротивлений соответствующих областей).
Аналитические выражения такие же как и для биполярного транзистора типа n-p-n.
Для математической модели схемы задания, можно упростить модель биполярного транзистора.
Упрощенная схема примет вид:
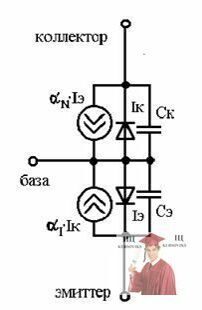
Составим эквивалентную схему замещения всего усилителя тока.
С учетом того, что количество узлов по возможности не должно быть более 6.
2. Модель трансформатора в для различных режимов работы
Модель трансформатора представлена на рисунке:
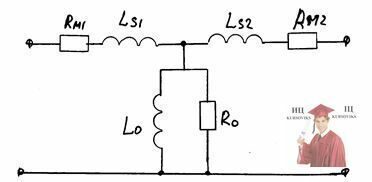
Где Rм1 -сопротивление меди первичной обмотки
Rм2 -сопротивление меди вторичная обмотки
Ls1 - индуктивность рассеяния первичной обмотки
Ls2 - индуктивность рассеяния первичной обмотки
Lо - индуктивность основного потока
Rо - потери в стали
В упрощенной схеме трансформатора можно принебреч сопротивлением меди.
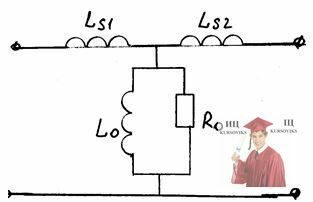
Запишем нелинейные функции:
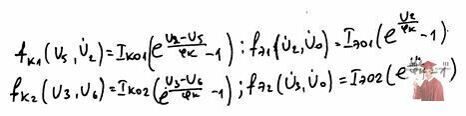
3. Статический режим работы схемы
Статический режим работы схемы является режимом по постоянному току, по этому производные напряжений будут dU/dt=0, а источник переменного тока J=0.
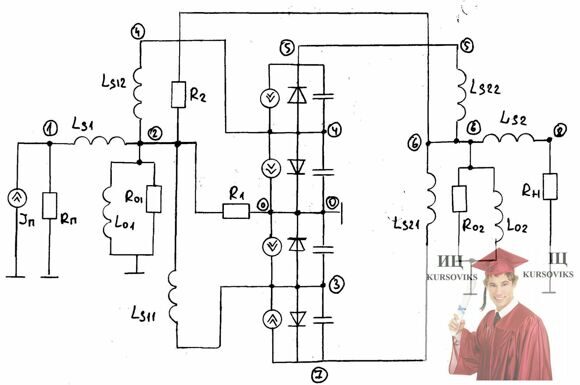
Составим схему эквивалентную схему замещения для описания математических моделей режимов работы в статическом режиме. Схема замещения для статического режима.
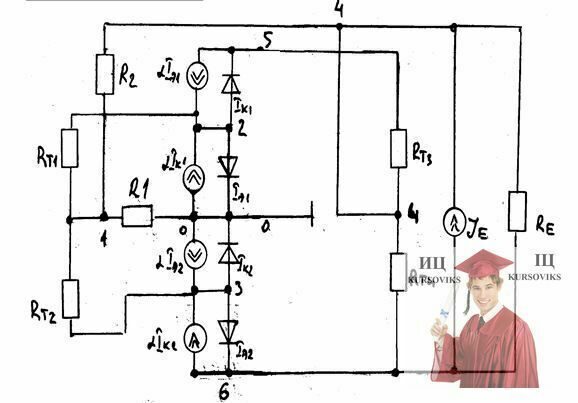
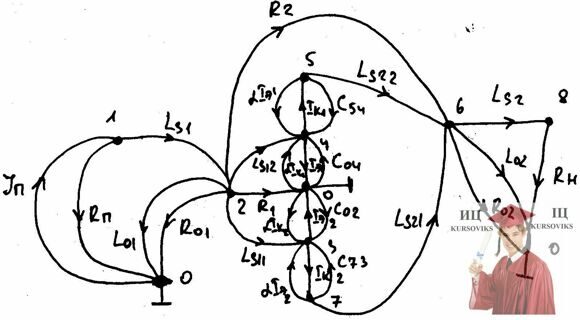
По эквивалентной схеме замещения составим граф для статического режима.
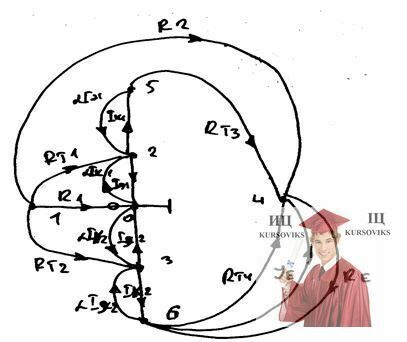
Запишем систему математических уравнений статического режима схемы.

Система может быть решена с помощью метода Ньютона или Ньютона-Рафсона.

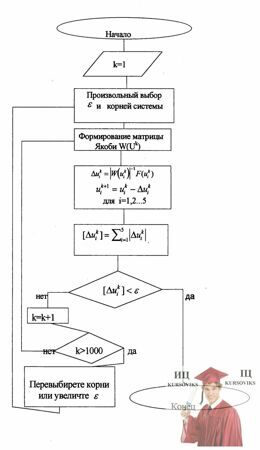
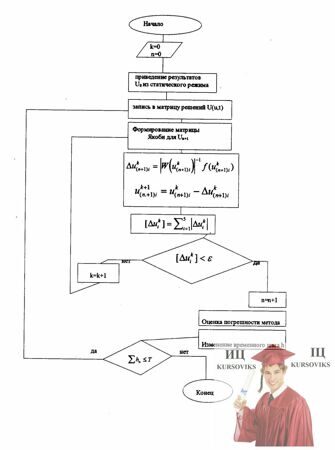
Уравнения статического режима данной схемы можно решить методом Ньютона. Суть этого метода состоит в том, что имеется матрица некоторых переменных (V1, V2, …,Vn) существует область, где находятся эти переменные М. Сначала находим первое приближение (V1º, V2º, …, Vnº ), из условия ¦(V1º, V2º, …, Vnº) = 0; после этого ищем следующее приближение (V1¢, V2¢, …, Vn¢), т.е. Viк = Viк-1 - ôW(Viк-1)ô-1 ¦( Viк-1), где
i – номер узлов схемы (i = 1, …n)
к – число итераций (к = 0,1 … m)
Затем из системы уравнений определяем Δ Viк
Δ Viк = - ôW(Viк)ô-1 ¦( Viк), где
W – Якобиан системы уравнений.
Интеграции повторяют до тех пор, пока максимальное приращение [Δ Viк] ≥ e, где e – выбранная погрешность, а [Δ Viк] – максимальное отклонение на к-ом шаге: [Δ Viк] = maxi [Δ Viк]. Выше сказанное можно описать алгоритмом который будет представлен ниже.
Якобиан системы уравнений для статического режима и значения элементов Якобиана:

4. Алгоритм решения системы нелинейных уравнений методом Ньютона
5. Cхема при воздействии большого сигнала. Временная область
Эквивалентная схема для большого сигнала:
Граф для большого сигнала:
При воздействии большого сигнала математическая модель работы схемы имеет вид:
Система уравнений может быть решена с помощью неявного метода Эйлера.
Суть метода заключается в нахождении прогнозируемого значения U, после чего его корректируют. Применив этот метод к системе уравнений можно найти решение в момент времени (t0,t1,…. tn)
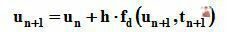
где un – искомое значение величины в данный момент времени;
un+1 – прогнозируемое значение в последующий момент времени;
h – временной шаг h=Dt= tn+1 – tn.
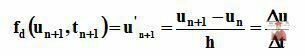
Подставим это в систему уравнений тогда вместо системы уравнений F(u’,u,t)=0 мы получаем систему 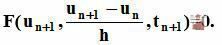 .
.
Данную систему можно решить методом Ньютона, который был описан выше. Систему будем решать относительно un+1
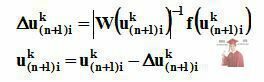
Таким образом расчет динамического режима сводится к многократному (n раз) решению на каждом шаге численного интегрирования системы линейных алгебраических уравнений.
Можно описать алгоритм метода Эйлера, который будет представлен ниже.

Якобиан системы уравнений и значение элементов Якобиана системы уравнений для большого сигнала временной области.
6. Алгоритм решения системы нелинейных уравнений методом Эйлера
7. Cхема при воздействии малого сигнала. Временная область
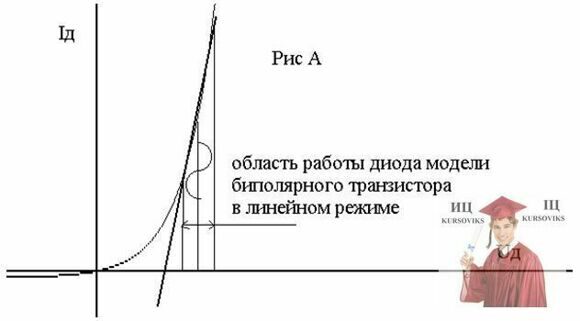
При воздействии малого сигнала все нелинейные элементы схемы линеаризуются. В предложенной для анализа схеме необходимо линеаризовать диодные характеристики схем замещения биполярных транзисторов, то есть диоды можно заменить линейной функцией, как показано на рисунке А,
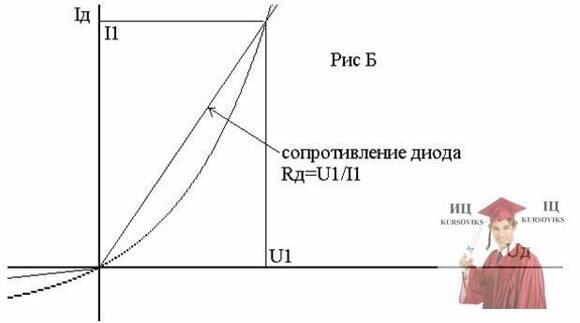
или сопротивлением диода, как показано на рисунке Б.
Из рисунков видно, что более точно смоделировать работу диодной характеристики биполярного транзистора с помощью линейной функции Iд=а*Uд+b, где производная I'д=а. Однако использование линеаризации, представленной на рисунке Б, чаще используется и дает при расчетах допустимое приближение по точности расчета.
Линеаризация примет вид:
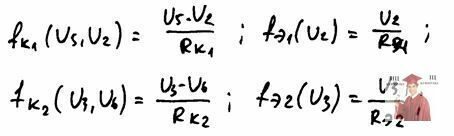
Система уравнений в линейном режиме примет вид:
8. Cхема при воздействии большого сигнала. Частотная область
Для анализа схемы в частотной области при воздействии большого сигнала, необходимо представить все переменные входящие в уравнения токов в комплексной форме, производные заменить на d/dtÛ(j*w)
uÛU- комплексное напряжение, iÛI-комплексное значение тока
Система перепишется в виде:
9. Cхема при воздействии двух гармонически не связанных больших сигналов. Частотная область
Математически в систему уравнений остается такая же как и при воздействии одного большого сигнала, за исключением того, что вводится еще один источник энергии.
Система перепишется в виде:
Решить полученные системы уравнений можно используя метод гармонического баланса. Метод гармонического баланса вытекает из методов Галеркина и Рица, основанных, как и разложение в ряд Фурье, на аппроксимации решения интегро-дифференциального уравнения линейной комбинацией базисных функций. Метод гармонического баланса требует, чтобы исходные уравнения удовлетворялось по всем частотам рассматриваемого спектра колебаний.
При воздействии на нелинейную схему n узкополосных гармонических сигналов с частотами w1,w2,...,wn в ней возникает сложное колебание, спектр которого содержит бесконечное множество составляющих кратных и комбинационных частот:
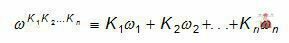
где Ki - целые числа;
K1K2...Kn - номер гармоники.
Однако, учет избирательных свойств элементов реальной цепи позволяет при использовании протекающих в ней процессов ограничивается учетом лишь незначительного количества составляющих спектра колебания (приравнивая нулю остальные весьма малые компоненты). Поэтому при воздействии n узкополосных сигналов М ненулевых гармоник (основных, кратных и комбинационных) образуют конечное дискретное множество частотных точек  .
.
Связь между дискретными многомерными отсчетами временной зависимости и ее спектральными составляющими устанавливается парой многомерных преобразований Фурье:
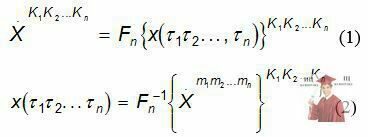
где 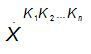 - гармоническая составляющая, соответствующая частоте
- гармоническая составляющая, соответствующая частоте 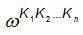 ;
;
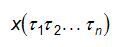 - дискретный многомерный отсчет периодически изменяющейся переменной x;
- дискретный многомерный отсчет периодически изменяющейся переменной x;
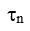 - безразмерная величина, играющая роль временной переменной и изменяющаяся от 0 до 2p(rn=wnt);
- безразмерная величина, играющая роль временной переменной и изменяющаяся от 0 до 2p(rn=wnt);
- · - знак комплексной амплитуды.
Выражение (1) определяет прямое преобразование Фурье изменяющейся во времени переменной x для гармоники с номером К1К2....Кn:
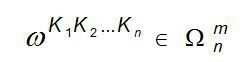
Соотношение (2) позволяет вычислить n - мерный отсчет в дискретный момент 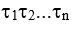 для переменной х, заданной спектральными составляющими (обратное преобразование Фурье):
для переменной х, заданной спектральными составляющими (обратное преобразование Фурье):
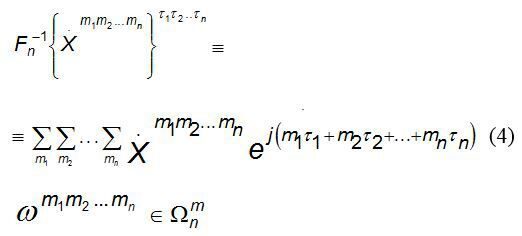
Следует отметить, что преобразование (4) позволяет получить лишь гипотетический отсчет периодической величины х. Для вычисления одномерной упорядоченной последовательности х(t) необходимо применять модифицированное преобразование:
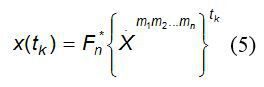
определяющее сворачивание многомерного пространства в одномерное:
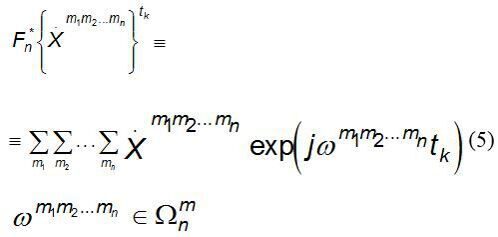
Лишь при моногармоническом воздействии:
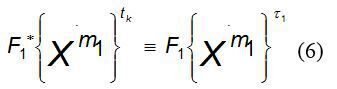
Во всех остальных случаях при вычислении времязависимых качественный показателей режима работы схемы приходится пользоваться трудоемким вспомогательным преобразованием (5).
Преобразование Фурье относится к классу линейных преобразований. Поэтому
где x и y - периодические функции;
a и b - произвольные константы.
10. Cхема при воздействии малого сигнала. Частотная область
Для анализа схемы в частотной области при воздействии малого сигнала, необходимо линеаризовать нелинейные функции, как и в случае малого сигнала во временной.
Для анализа схемы в частотной области при воздействии большого сигнала, необходимо представить все переменные входящие в уравнения токов в комплексной форме, производные заменить на d/dtÛ(j*w),
uÛU- комплексное напряжение, iÛI-комплексное значение тока
Система перепишется в виде:
Обычно систему решают методом Гаусса или Крамера с комплексными переменными.
Приложение
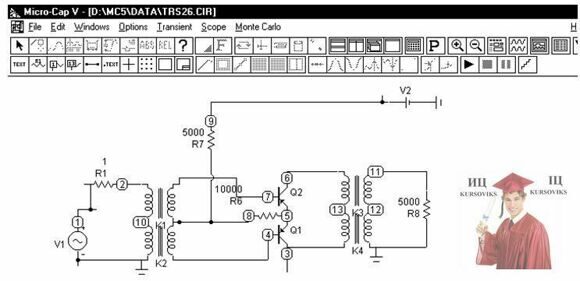
Анализ режимов схемы с применением програмного комплекса "MICROCAP-5"
Расчетная схема режимов работы (один источник)
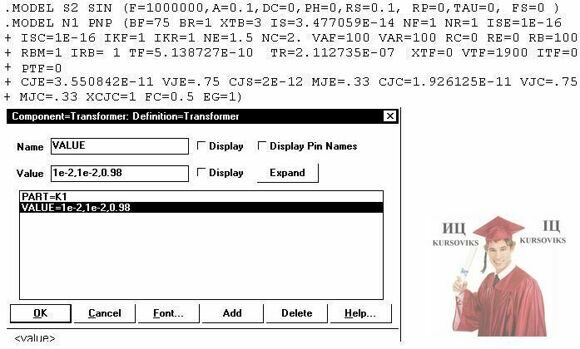
Параметры схемы
ЛИНЕЙНЫЙ РЕЖИМ РАБОТЫ Uвх -> Uвых (узел 1 и узел 11)
(Временная область малый сигнал)
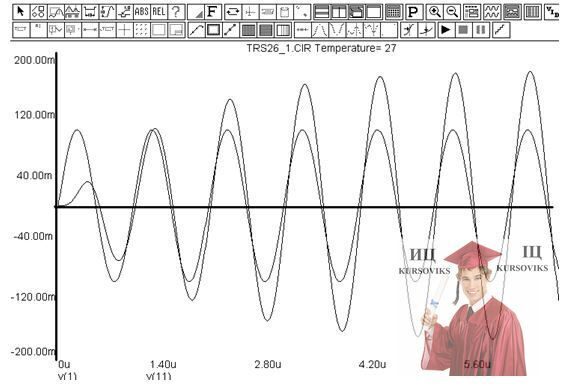
ТОК ВХОДА R1 и ТОК ВЫХОДА R8
(Временная область малый сигнал)

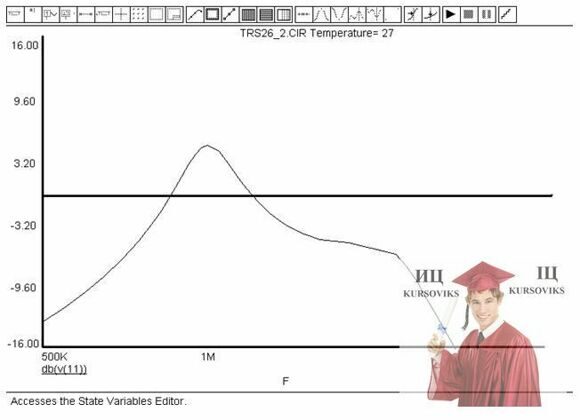
УСИЛЕНИЕ ПО НАПРЯЖЕНИЮ УЗЕЛ 11
(Частотная область)
ИЗМЕНЕНИЕ ФАЗЫ ОТ ЧАСТОЫ УЗЕЛ 11
(Частотная область)
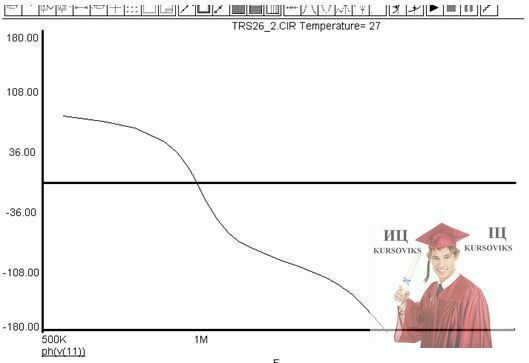
НЕЛИНЕЙНЫЙ РЕЖИМ РАБОТЫ Uвх -> Uвых (узел 1 и узел 11)
(Временная область)
Нелинейный режим ток входа R1 и ток выхода R8
(временная область)

Усиление по напряжению узел 11. Нелинейный режим
(частотная область)
Изменение фазы от частоы узел 11. Нелинейный режим

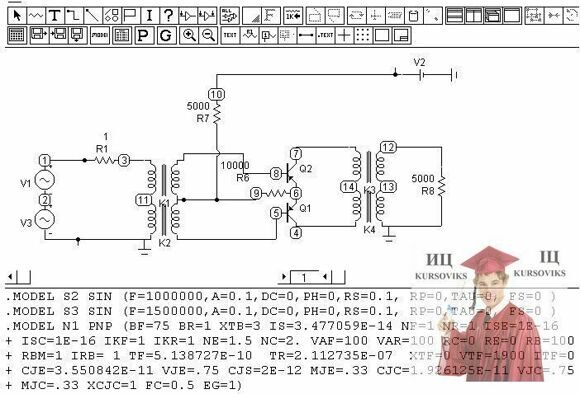
РАСЧЕТНАЯ СХЕМА РЕЖИМОВ РАБОТЫ (ДВА ИСТОЧНИКА)
ПАРАМЕТРЫ и ПАРАМЕТРЫ СХЕМЫ
ЛИНЕЙНЫЙ РЕЖИМ РАБОТЫ Uвх -> Uвых (узел 3 и узел 12)
(Временная область малый сигнал)

ЛИНЕЙНЫЙ РЕЖИМ ТОК ВХОДА R01 и ТОК ВЫХОДА R2
(Временная область малый сигнал)
НЕЛИНЕЙНЫЙ РЕЖИМ РАБОТЫ Uвх -> Uвых (узел 3 и узел 12)
(Временная область малый сигнал)