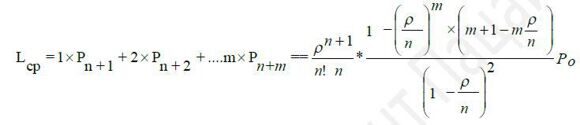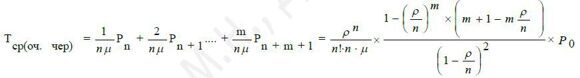Лабораторна робота №17-18, Системи масово обслуговування
Код роботи: 964
Вид роботи: Лабораторна робота
Предмет: Дослідження операцій
Тема: №17-18, Системи масово обслуговування
Кількість сторінок: 1
Дата виконання: 2016
Мова написання: українська
Ціна: 350 грн (за Excel)
Теоретична довідка
Діяльність будь-якого торгівельного підприємства, перш за все, пов'язана з обслуговуванням покупців. Успішність його діяльності багато в чому визначається оптимальною організацією роботи продавців, кількістю зон обслуговування потоку покупців, своєчасного розвантаження товарів, що поступають, і ін.
Основною ознакою такої діяльності є існування деякої обслуговуючої системи (системи масового обслуговування (СМО)), яка забезпечує обробку тих, що поступають в неї потоку заявок на обслуговування. Як правило, заявки в систему поступають нерегулярний (випадковим чином) і, враховуючи те, що будь-яка обслуговуюча система має обмежені можливості, періодично (інакше вона виявляється збитковою) в системі можуть виникати черги на обслуговування, а частина заявок може дістане відмову, а в окремих випадках просто простоювати із-за відсутності заявок (покупців).
У зв'язку з цим, одним з критеріїв роботи торгівельного підприємства є час виконання окремих операцій по обслуговуванню покупців.
Для населення витрати часу на покупку включають час на дорогу, повторні відвідини магазина, вибір товару, чекання в чергах, оплату і упаковку товару і ін.
Проведені дослідження структури витрат часу як продавців так і покупців говорять про те, що значна частина часу витрачається непродуктивно. Так наприклад, за оцінкою економістів на чекання в чергах покупці витрачають більше 25 -30% часу і практично стільки ж на - чекання черги на оплату і упаковку придбаного товару.
Як інший приклад може бути приведене завдання визначення кількості розрахункових вузлів (кас), необхідних для якісного і економічно виправданого обслуговування покупців. Оптимальним варіантом рішення задачі буде той, при якому час обслуговування буде мінімальним; якість – високим; витрати на створення місць обслуговування і їх роботу мають бути мінімальними.
Подібні завдання можуть вирішуватися з використанням математичного апарату теорії систем масового обслуговування.
Основні положення теорії систем масового обслуговування (СМО).
Системи масового обслуговування можна розділити на трьох типів:
СМО з відмовами. Особливістю систем такого типа є те, що
- час чекання заявок (k) в черзі tчер = 0,
- оскільки існування черги неможливе, довжина черги Iчер = 0,
- ймовірність виникнення черги на обслуговування заявок (покупців.) Рчер = 0.
За відсутності заявок на обслуговування (k=0) – спостерігається простій каналів;
При – відбувається обслуговування заявок;
При k > n відбувається виконання заявок, утворення черги і відмова у виконанні заявок, що поступили, на обслуговуванні (при зайнятості всіх каналів).
Основними показниками таких СМО є:
- Рвідм – ймовірність відмови в обслуговуванні заявок, що поступили;
- Робс – ймовірність обслуговування заявок, що поступили;
- Р0 – ймовірність простою каналів обслуговування (відсутність заявок);
- tпр - середній час простою каналу обслуговування;
- tобсл – середній час обслуговування;
- nзайн і nвіл – кількість зайнятих і вільних каналів обслуговування, відповідно;
- А – абсолютна пропускна спроможність СМО.
Для СМО з необмеженим очікуванням характерно, що ймовірність обслуговування заявки Робс =1, оскільки будь-яка заявка, що поступила, рано чи пізно буде обслужена.
Така СМО може мати наступні стани:
при k = 0 – система простоює (знаходиться в режимі чекання заявок);
при 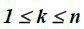 - обслуговування;
- обслуговування;
при k > n – утворюється черга.
Основні показники:
- Lчер – середнє число заявок в черзі;
- Z – середнє число заявок в СМО;
- Tсмо – середній час перебування заявки в СМО;
- А – абсолютна пропускна спроможність СМО.
Для СМО з очікуванням і обмеженням на довжину черги (max Lчер=m) при:
при k = 0 – система простоює (знаходиться в режимі чекання заявок);
при 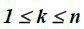 - обслуговування;
- обслуговування;
при 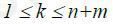 – обслуговування, черга і відмова в обслуговуванні.
– обслуговування, черга і відмова в обслуговуванні.
Основні показники:
- Рвідм – ймовірність відмови в обслуговуванні заявок, що поступили;
- Робс – ймовірність обслуговування заявок, що поступили;
- Lчер – середнє число заявок в черзі;
- Z - середнє число заявок в СМО;
- Tсмо – середній час перебування заявки в СМО;
- А – абсолютна пропускна спроможність СМО.
1. Визначення інтенсивності потоку заявок і завантаження каналів обслуговування
Однією з найважливіших характеристик СМО є потік заявок. Ця характеристика визначає порядок обслуговування заявок, що поступають на вхід системи. Найчастіше використовується порядок черги – «першим прийшов – першим обслужений».
Для визначення середньої величини інтенсивності потоку заявок на обслуговування проводяться хронометражні виміри потоку заявок на обслуговування за одиницю часу.
Наприклад, розглянемо ситуацію, коли протягом 10 днів робився підрахунок кількості покупців, що приходять в магазин протягом кожної години.

Рис. 1 - Структурна модель елементарної СМО
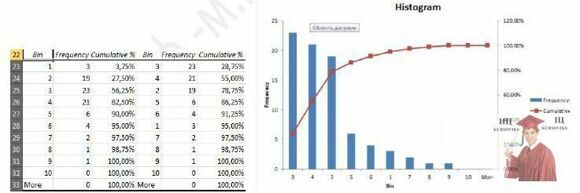
Для обчислення інтенсивності потоку покупців 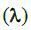 згрупуємо дані по числу покупців (k), що відвідали магазин протягом години (визначимо частоту відвідин магазина покупцями). Іншими словами, ми повинні побудувати гістограму частоти відвідин магазина покупцями.
згрупуємо дані по числу покупців (k), що відвідали магазин протягом години (визначимо частоту відвідин магазина покупцями). Іншими словами, ми повинні побудувати гістограму частоти відвідин магазина покупцями.
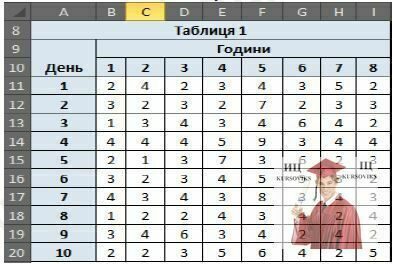
Рис. 2 - Фрагмент аркуша Excel з таблицею частоти відвідин магазина покупцями
- Виконаєте команду ДАННЫЕ (АНАЛІЗ ДАНИХ).
- У діалоговому вікні, що відкрилося, АНАЛІЗ ДАНИХ виберіть ПП Гістограма.
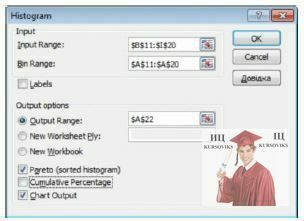
Рис. 3 - Діалогове вікно Гістограма
У діалоговому вікні, що відкрилося, Гістограма виконаєте необхідні установки:
- у вікно «Input range» введіть адреси комірок, що містять значення відвідуваності магазина покупцями (у нашому прикладі – комірки B11:I20);
- у вікно «Bin range» введіть діапазон вічок і набір значень, що визначають відрізки. Ці значення мають бути введені в зростаючому порядку. У Microsoft Excel обчислюється число попадань даних між поточним початком відрізання і сусіднім великим по порядку, якщо такий є. При цьому включаються значення на нижньому кордоні відрізання і не включаються значення на верхньому кордоні . У нашому прикладі, як інтервал кишень вкажемо адреси А11:А20, що містять числа від 1 до 10, розташовані в зростаючому порядку.
- У вікно «Output range» введіть посилання на ліву верхню комірку вихідного діапазону. Розмір вихідного діапазону буде визначений автоматично, і на екран буде виведено повідомлення в разі можливого накладення вихідного діапазону на вихідні дані. У нашому прикладі, вкажемо адресу А22.
При бажанні
- встановіть прапорці «Paretto (відсортована диаграмма)»- дані будуть представлені в порядку зменшення частоти. Якщо прапорець знятий, то дані у вихідному діапазоні будуть представлені в порядку зростання відрізків, а трьох найправіших стовпців з відсортованими даними не буде;
- Інтегральний відсоток. Встановите прапорець для генерації інтегральних процентних відношень і включення в гістограму графіка інтегральних відсотків. Зніміть прапорець, аби не обчислювати інтегральні процентні співвідношення.
- Виведення графіка. Встановите прапорець для автоматичного створення вбудованої діаграми на аркуші, що містить вихідний діапазон.
В результаті виконаних дій Excel таблицю розподілу частот відвідин магазина покупцями.
Рис. 4 - Фрагмент аркуша Excel з таблицею розподілу частот відвідин магазина покупцями
Інтенсивність потоку покупців може бути знайдена як суммпроизв числа відвідин (Bin) на спостережувану частоту відвідин (f) ділене на загальне число відвідин:
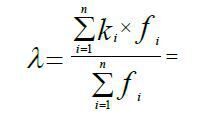 (1)
(1)
У нашому прикладі кількість покупців в одиницю часу визначається як:
а середній час приходу одного покупця визначиться як
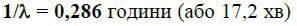
Подібним же чином можуть бути визначений середній час обслуговування покупців продавцями (tобсл) і інтенсивність обслуговування 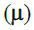 – середня кількість клієнтів, що обслуговуються в одиницю часу
– середня кількість клієнтів, що обслуговуються в одиницю часу
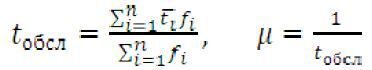 (2)
(2)
У випадку, коли 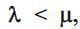 (тобто, частота подачі заявок нижча за інтенсивність обслуговування часу їх обслуговування) черги не виникає, оскільки задоволення вимог відбувається не раніше їх появи.
(тобто, частота подачі заявок нижча за інтенсивність обслуговування часу їх обслуговування) черги не виникає, оскільки задоволення вимог відбувається не раніше їх появи.
2. Аналіз функціонування системи масового обслуговування
Вважаючи, що покупці прибувають в магазин «випадково» можна вважати, що ймовірність прибуття покупця за будь-який малий проміжок часу 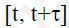 , що починається в довільний момент часу t і має тривалість
, що починається в довільний момент часу t і має тривалість 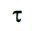 з точністю до нехтує малих величин пропорційно величині
з точністю до нехтує малих величин пропорційно величині 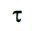 з деяким коефіцієнтом
з деяким коефіцієнтом 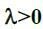 . Ймовірність того, що за цей проміжок часу в магазин не прибуде жодного покупця може бути приблизно оцінена як
. Ймовірність того, що за цей проміжок часу в магазин не прибуде жодного покупця може бути приблизно оцінена як 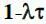 .
.
Виходячи з цього, в теорії ймовірності робляться висновки:
проміжки часу (між двома покупцями відповідають експоненціальному розподілу
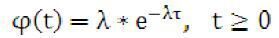
ймовірність того, що за будь-який проміжок часу Т в магазин прибуде k покупців (клієнтів, заявок) може бути визначена як
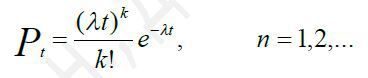
тобто вхідний потік покупців є пуассоновским.
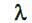 - інтенсивність вхідного потоку, тобто середнє число заявок, що поступають в СМО за одиницю часу.
- інтенсивність вхідного потоку, тобто середнє число заявок, що поступають в СМО за одиницю часу.
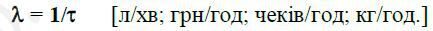
де 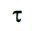 - середнє значення інтервалу часу між двома сусідніми заявками (появою покупців).
- середнє значення інтервалу часу між двома сусідніми заявками (появою покупців).
Випадковий час очікування в черзі початку обслуговування теж можна вважати розподіленим експоненціально.
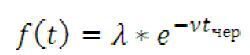
де 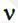 - інтенсивність руху черги (середнє число заявок, що поступають на обслуговування в одиницю часу);
- інтенсивність руху черги (середнє число заявок, що поступають на обслуговування в одиницю часу);
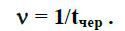
tчер – середнє значення часу чекання в черзі.
Вихідний потік заявок (заявок, що пройшли обслуговування) пов'язаний з потоком обслуговування в каналі СМО також, в більшості випадків, підкоряється закону розподілу з щільністю
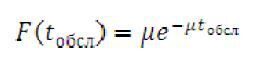 (3)
(3)
де 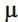 - інтенсивність обслуговування в каналі (одним продавцем.), тобто середнє число заявок (клієнтів), що обслуговуються в одиницю часу.
- інтенсивність обслуговування в каналі (одним продавцем.), тобто середнє число заявок (клієнтів), що обслуговуються в одиницю часу.
![]()
Одній з найбільш важливих характеристик СМО, що зв'язує показники 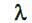 і
і 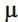 – інтенсивність навантаження
– інтенсивність навантаження 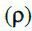 ,
,
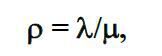 (4)
(4)
яка показує міру узгодженості вхідного потоку заявок з інтенсивністю їх обслуговування.
Величину 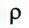 часто називають приведеною щільністю потоку вимог (заявок) або інтенсивністю навантаження – середнє число вимог, що припадає на середній час обслуговування однієї вимоги.
часто називають приведеною щільністю потоку вимог (заявок) або інтенсивністю навантаження – середнє число вимог, що припадає на середній час обслуговування однієї вимоги.
Важливо відмітити, що параметр 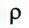 характеризує міру узгодженості вхідного потоку (наприклад, покупців в магазині) з інтенсивністю потоку обслуговування. Процес обслуговування буде стабільний при
характеризує міру узгодженості вхідного потоку (наприклад, покупців в магазині) з інтенсивністю потоку обслуговування. Процес обслуговування буде стабільний при 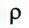 < n. Якщо ж
< n. Якщо ж 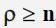 , то в системі зростатиме середня довжина черги і середній час чекання покупців початку обслуговування, і, отже, проектована СМО працюватиме нестійкий.
, то в системі зростатиме середня довжина черги і середній час чекання покупців початку обслуговування, і, отже, проектована СМО працюватиме нестійкий.
Розглянемо найбільш загальний випадок СМО, коли n – канальна система працює в режимі з чеканням обслуговування і з обмеженням на довжину черги (у черзі не може бути більш за m вимог). При цьому, ми передбачаємо, що вхідний потік вимог на обслуговування описується пуассоновским законом розподілу з інтенсивністю 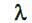 , а час обслуговування вимог розподілений по показниковому закону з інтенсивністю
, а час обслуговування вимог розподілений по показниковому закону з інтенсивністю 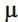 .
.
Ймовірність того, що в системі відсутні вимоги (Р0) може бути визначена по формулі:
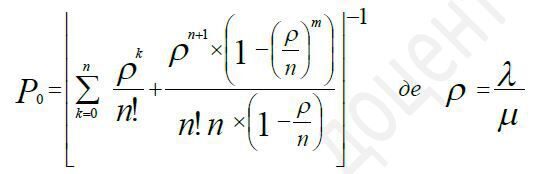 (5)
(5)
Ймовірність того, що в системі обслуговування знаходяться k вимог на обслуговування (Pk) може бути визначена як:
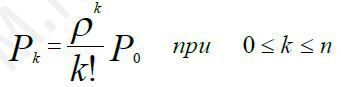 (6)
(6)
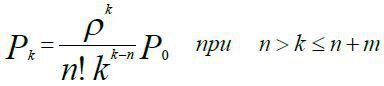 (7)
(7)
Відношення 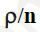 часто позначається через Х і називається рівнем завантаження системи.
часто позначається через Х і називається рівнем завантаження системи.
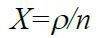 (8)
(8)
Якщо Х <1, то черга на обслуговування не утворюється і система знаходиться в стаціонарному стані, який характеризується тим, що ймовірність вступу певної кількості вимог в перебігу заданого проміжку часу залежить лише від його тривалості.
Ймовірність відмови в обслуговуванні вимоги (заявки, клієнта.), якщо в систему поступає n+m заявок на обслуговування
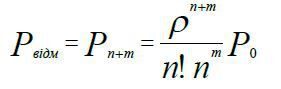 (9)
(9)
Ймовірність обслуговування заявки, що поступила (або відносна пропускна здатність СМО)
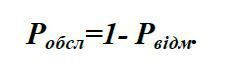 (10)
(10)
Абсолютна пропускна здатність системи (число фактично обслужених вимог за одиницю часу)
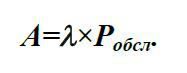 (11)
(11)
Середнє число зайнятих каналів обслуговування
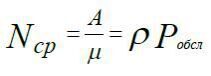 (12)
(12)
оскільки А – це інтенсивність потоку обслуговування заявок, а кожен канал здатний в одиницю (в середньому) обслуговувати 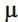 заявок.
заявок.
Коефіцієнт використання (зайнятості) каналів
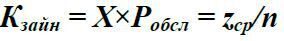 (13)
(13)
Коефіцієнт простою каналів обслуговування
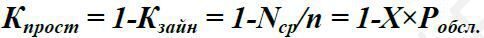 (14)
(14)
Середнє число вимог (заявок) в черзі
Середній час обслуговування вимог
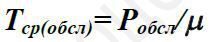 (16)
(16)
Середній час чекання в черзі
Оскільки, якщо заявка на обслуговування поступить в той момент, коли всі канали зайняті і черги немає, то час чекання складе в середньому 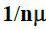 , а якщо заявка поступить в той момент, коли в черзі знаходиться одна вимога на обслуговування,
, а якщо заявка поступить в той момент, коли в черзі знаходиться одна вимога на обслуговування, 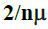 і так далі.
і так далі.
Середній час перебування заявки в СМО
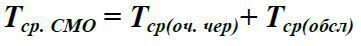 (18)
(18)
Утворення черги можливе лише тоді, коли заявка, що знов поступила, застане на обробці в системі не менше n вимог на обслуговування, тобто коли в СМО знаходитиметься n, n+1, n+2, n+m-1 вимог на обслуговування. Враховуючи те, що заявки в СМО поступають незалежно один від одного, ймовірність того, що всі канали обслуговування будуть зайняті дорівнює сумі вірогідності Рn, Pn+1, Pn+2….Pn+m-1.
Звідси ймовірність утворення черги:
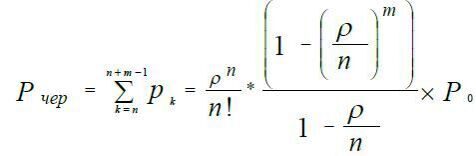 (19)
(19)
Вище були приведені формули для розрахунку основних характеристик СМО для випадку, в якому допускається виникнення черги за наявності обмеження на її довжину.
Якщо m=0, то ми маємо справу з першим частним злучаємо СМО – системи з відмовами. Найбільш типовим прикладом такої СМО є робота столу замовлень (або довідкової служби) по телефону – якщо всі телефони зайняті прийомом замовлень, то дзвінок нового покупця дістає відмову – сигнал зайнято.
У тому випадку, коли 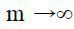 , то отримуємо СМО з чеканням без обмеження на довжину черги.
, то отримуємо СМО з чеканням без обмеження на довжину черги.
3. Критерії якості функціонування СМО
Значна частина показників функціонування СМО, визначені в попередньому розділі, суперечливі в тому сенсі, що поліпшення одних показників неминуче веде до погіршення інших. Наприклад, скорочення довжини черги (або часу чекання початку обслуговування) шляхом збільшення числа каналів обслуговування (збільшення кількості продавців, телефонів, підсобних приміщень і ін.) пов'язане з погіршенням таких показників як збільшення часу простою каналів, збільшенню витрат на їх вміст і ін. Таким чином, необхідно проектувати СМО так, щоб досягти розумного компромісу між показниками власне заявок і використанням можливостей СМО, т.е необхідно мати критерій, що дозволяє оцінити якість роботи СМО з цих позицій.
У простому випадку (наприклад, для систем з відмовою) таким критерієм може бути вибрана ймовірність відмови в обслуговуванні (Рвідм), Можна зажадати, аби Ротк не перевищувала заздалегідь заданої величини. Наприклад вимога Ротк < 0,1 означає, що СМО, при заданій інтенсивності потоку заявок 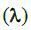 , справлятиметься з їх обслуговування не менше чим в 90% від їх загального числа.
, справлятиметься з їх обслуговування не менше чим в 90% від їх загального числа.
Можна зажадати обмеження середнього часу перебування заявки в черзі (або системі).
Як параметра- критерій може виступати або число каналів n при заданій інтенсивності обслуговування заявок 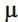 , або інтенсивність обслуговування
, або інтенсивність обслуговування 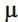 при заданому числі каналів, або найкращий варіант з n1, n2 n3, каналів з інтенсивністю обслуговування
при заданому числі каналів, або найкращий варіант з n1, n2 n3, каналів з інтенсивністю обслуговування 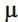 1,
1, 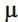 2,
2, 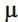 з.
з.
Як узагальнений критерій, що враховує всі суперечливі спрямованості показників роботи СМО, може бути вибраний показник, що характеризує її економічну ефективність. Що включає як витрати звернення (Свитр. зверн), так і витрати заявок (Свитр.заявок), які набуватимуть мінімального значення при мінімумі загальних витрат (Свитр).
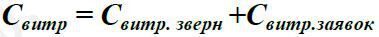
Оскільки при оцінці витрат необхідно враховувати не лише втрати, пов'язані з відмовами (або виникненням черг), але втрати, викликані витратами від простою каналів в очікуванні обслуговування, а також з витратами експлуатації СМО, узагальнений критерій якості роботи СМО може бути записаний таким чином:
де Секспл – витрати, пов'язані з експлуатацією системи;
Nс – середня кількість каналів, зайнятих обслуговуванням;
Спрост – витрати, пов'язані з простоєм каналів обслуговування;
Свідм – витрати, пов'язані з відмовою в обслуговуванні (втратою клієнтів);
Ссист – витрати, пов'язані з перебуванням заявки в СМО;
Тср.СМО – середнє. час перебування заявки в системі.
Слід зауважити, що як критерій ефективності роботи СМО (цільової функції) може виступати товарообіг підприємства (наприклад. рентабельність) Тоді, вочевидь, оптимальні значення керованих показників СМО знаходяться вже при їх максимальному значенні і необхідно відповідним чином провести перетворення цільової функції.
Після побудови цільової функції необхідно визначити умови рішення задачі, тобто знайти обмеження, встановити вихідні значення показників, виділити некеровані показники і побудувати (або підібрати) сукупність моделей взаємозв'язку всіх показників для аналізованого типа СМО, аби кв. кінцевому висновку знайти оптимальні значення показників, наприклад кількість продавців, касирів, підсобних робітників, фасують, об'єми складських приміщень і ін.
Хід лабораторної роботи
Розрахунок основних характеристик СМО
Приклад 1
Постановка
У торгівельному залі фірми обслуговуванням покупців займаються 2 продавці (n=2). На обслуговування одного покупця продавець в середньому витрачає 20 сек.(або 1/3 хв. Тобто (=3люд/хв)).
Інтенсивність вхідного потоку покупців складає 5 л/хв. (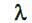 =5).
=5).
Керівництвом фірми встановлено, що довжина черги не повинна перевищувати 2 людини 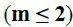 .
.
Використовуючи приведені вище формули визначити основні показники СМО.
1. На аркуші Excel розробимо таблицю вихідних даних, подібну приведеною на малюнку.
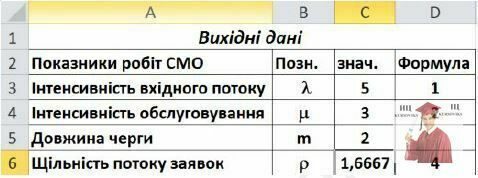
Рис. 5 - Фрагмент аркуша Excel з таблицею вихідних даних
У комірках С3:С5 розмістимо вихідні дані завдання.
У комірку С6 відповідно до формули (4) розрахуємо величину щільності потоку заявок 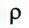 , записавши відповідну формулу.
, записавши відповідну формулу.
2. Розробимо таблицю розрахунку основних показників роботи СМО. Таблиця може мати вигляд, подібний показаному на малюнку.
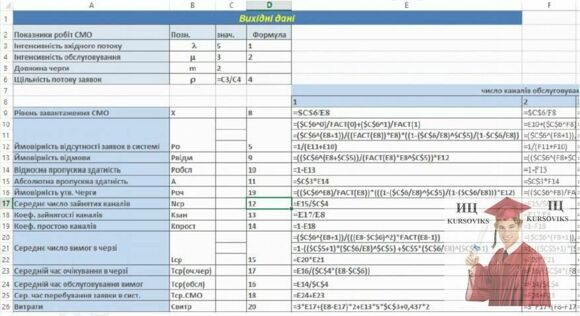
Рис. 6 - Фрагмент аркуша Excel з таблицею розрахунку основних показників СМО
Зауваження
Перш ніж записувати у комірки таблиці формули, уважно проаналізуйте їх і постарайтеся виділити в них елементи, що найчастіше зустрічаються. Це може не лише значно полегшити їх написання, але і дозволить уникнути зайвих помилок. Наприклад, у формулах досить частий зустрічається величина (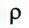 /n), може виявитися зручним в подальших обчисленнях використовувати саме її.
/n), може виявитися зручним в подальших обчисленнях використовувати саме її.
При записі досить складних формул (наприклад, таких як Р0 або Lч) виявляється зручними записувати їх частини в окремих комірках.
Наприклад, при записі формули може виявитися зручним в одній комірці записати
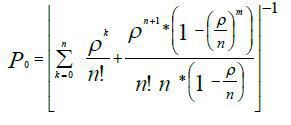
формулу для обчислення
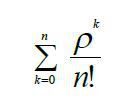
а в іншій комірці обчислити
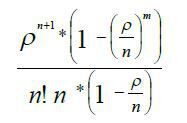
і тільки тоді знаходимо значення Р0.
У комірку Е9 запишіть формулу =$C$6/E8, значення Х – рівня завантаження СМО;
У комірку Е10 введіть формулу для обчислення
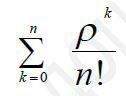
![]()
у комірку F10 розмістите формулу =E10+($C$6^F8)/ФАКТР(F8);
скопіюйте вміст комірки F10 у комірки G10:I10
У комірку Е11 запишіть формулу
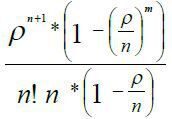
=($C$6^(E8+1))/((FACT(E8))*E8)*((1-($C$6/E8)^$C$5)/(1-$C$6/E8));
У комірку Е12 запишіть формулу =1/(E10+E11), що реалізовує обчислення ймовірності відсутності вимоги в СМО (Р0).
У комірці Е13 введіть формулу обчислення Рвідм
=(($C$6^(E8+$C$5))/(FACT(E8)*E8^$C$5))*E12 і скопіюйте її у комірки
F13:I13
У комірці Е14 введіть формулу обчислення Робсл =1-E13 і скопіюйте її у комірки F14:I14
У комірці Е15 розмістите формулу обчислення абсолютної пропускної спроможності (А) =$C$3*E14 і скопіюйте її у комірки F15:I15
У комірці Е16 розмістите формулу обчислення вірогідності відмови обслуговування заявки (ймовірність утворення черги (Рчер)
=(($C$6^E8)/FACT(E8))*(((1-($C$6/E8)^$C$5)/(1-($C$6/E8)))*E12) і скопіюйте її у комірки F16:I16
У комірці Е17 розмістите формулу обчислення середнього числа зайнятих каналів обслуговування (Nср) =E15/$C$4 і скопіюйте її у комірки F17:I17
У комірках Е18:Е19 розмістите формули для обчислення коефіцієнта зайнятості і простою каналів обслуговування (Кзайн і Кпрост), відповідно =E17/E8 і =1-E18. Скопіюйте їх у комірки F18:I19
У комірках E20:E21 розмістите частини формули для обчислення співмножників формули визначення довжини черги заявок (Lчер):
Е20 =($C$6^(E8+1))/(((E8-$C$6)^2)*FACT(E8-1))
і
Е21 =1-(($C$5+1)*($C$6/E8)^$C$5) +$C$5*($C$6/E8)^($C$5+1).
У комірці Е22 розмістите формулу, що реалізовує обчислення Lчер =E20*E21.
У комірках Е23:Е25 розмістите формули для обчислення середнього часу чекання в черзі; середнього часу обслуговування вимоги і середнього часу перебування вимоги в СМО (від моменту вступу вимоги до його виконання), відповідно.
Е23 =E16/($C$4*(E8-$C$6))
Е24 =E14/$C$4
Е25 =E24+E23
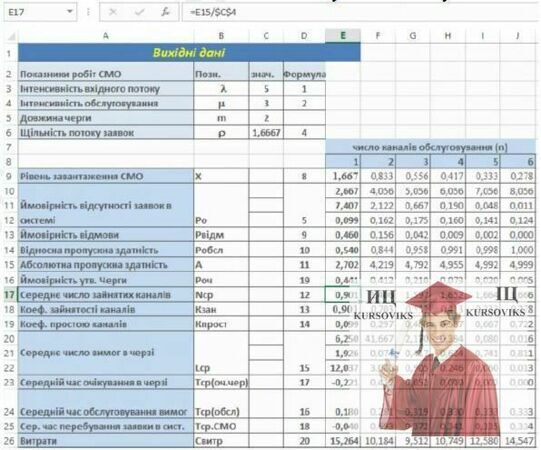
Таким чином, в результаті виконаних дій, на аркуші Excel буде отримана таблиця (рис.6) з даними, що характеризують роботу СМО.
З аналізу отриманої таблиці виходить, що за наявності двох продавців СМО знаходитиметься в стаціонарному режимі (X<0), проте, середня довжина черги складатиме Lср =3.086. При трьох продавцях середня довжина черги складе Lср = 0,905, що задовольняє умовам завдання. При цьому, ймовірність відмови в обслуговуванні покупців складе менше 5% (Рвідм =0,043)
Рис. 7 - Фрагмент робочого аркуша Excel з таблицею розрахунку основних показників СМО в режимі відображення формул
Примітка. Побудована таблиця може бути використана як шаблон при вирішенні інших завдань СМО.
Приклад 2
Овочевий магазин отримує овочі з теплиць приміських ферм. Автомобілі з вантажем прибувають протягом дня з інтенсивністю 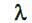 =6 автомашин в день.
=6 автомашин в день.
Підсобне приміщення і устаткування для фасовки овочів і підготовки їх до продажу дозволяють обробляти і зберігати товар, привезений двома автомобілями (m =2).
У магазині працюють 4 робітники (n = 3), кожен з яких на обробку вантажу з однієї машини витрачає в середньому 4 години. Тривалість робочої зміни складає 12 годин. (тобто 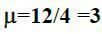 ).
).
Визначити яка має бути ємкість (кількість) підсобних приміщень (m=?) для того, щоб ймовірність повної обробки товарів 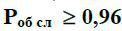 .
.
Хід роботи
Для вирішення завдання може бути використаний шаблон таблиці, створеної в попередньому прикладі.
У комірки В3, В4 і В5 введемо вихідні дані завдання 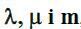 , відповідно.
, відповідно.
Після занесення вихідних даних на екрані відображуватимуть основні характеристики СМО завдання.
Як видно з даного рис., за заданих умов завдання ймовірність обслуговування Робсл = 0,885.
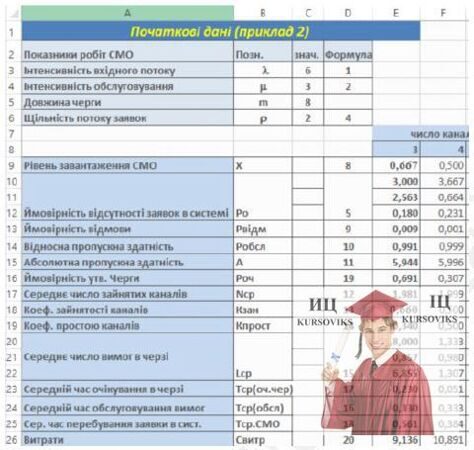
Рис. 8 - Фрагмент аркуша Excel з таблицею вихідних даних прикладу 2 і таблицею розрахунку основних характеристик СМО
Для визначення кількості необхідних підсобних приміщень (m), з метою досягнення заданої величини Робсл., скористаємося операцією побудови сценарію (команда ![]() і виконаємо розрахунки для значень m = 2, 3, 4, 5, 6, 7, 8, 9, 10.
і виконаємо розрахунки для значень m = 2, 3, 4, 5, 6, 7, 8, 9, 10.
Для визначення величини m ТАКОЖ можна скористатися засобом ПОДБОР ПАРАМЕТРА
За результатами розрахунків сценаріїв, побудуємо звіт, вибравши тип звіту – структурний і як комірки результату вкажемо адресу комірки, що містить значення Робсл(G14).
Рис. 9 - Діалогове вікно вибору побудови звіту за сценарієм
В результаті виконаних дій в робочу книгу Excel буде вставлений додатковий аркуш із звітом за сценарієм.
Виконаємо необхідне редагування звіту і побудуємо діаграму, що ілюструє зміну величини Робсл залежно від значення величини m.
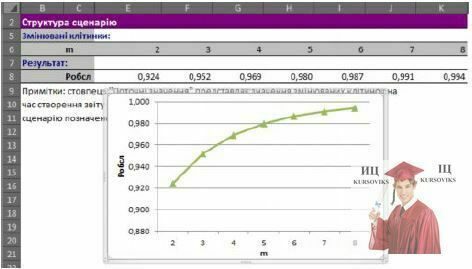
Рис. 10 - Фрагмент аркуша Excel із звітом за сценарієм
Як видно з таблиці звіту за сценарієм, необхідна величина Робсл може бути досягнута при збільшенні числа підсобних приміщень до m=4.
Відмітимо, що з таблиці, приведеної на рис.8. випливає, що необхідна величина Робсл може бути досягнута не збільшенням кількості підсобних приміщень, а збільшенням кількості робітників до n=4. Рішення цього питання залишається за Вами: що вигідно (доцільніше) прийняти додаткового робітника або орендувати (або використовувати порожнє) приміщення.
Приклад 3
Торгівельна фірма спеціалізується на продажі товарів при оформленні замовлень по телефону. Керівництво фірми для обслуговування клієнтів має намір придбати міні АТС, що забезпечує підключення трьох, п'яти або десяти телефонних апаратів. Витрати, пов'язані з експлуатацією цих МІНІ-АТС приведені в таблиці.
Інтенсивність потоку замовлень клієнтів складає 1.2 замовлення/хв. Інтенсивність обслуговування замовлень рівна 0,5 зам/хв.
Необхідно визначити, яка з Міні-АТС дозволить забезпечити найбільш ефективну роботу, при мінімальній величині витрат.
Хід роботи
Для вирішення задачі скористаємося шаблоном, розробленим при вирішенні прикладу 1.
У комірки В3, В4 і В5 введемо вихідні дані завдання 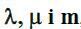 , відповідно.
, відповідно.
Після занесення вихідних даних на екрані буде відображено основні характеристики СМО завдання (рис.11)
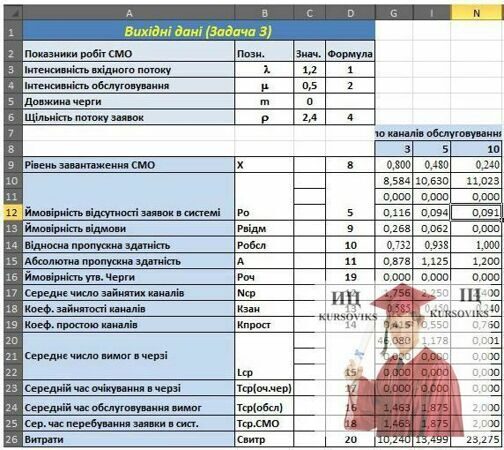
Рис.11 - Фрагмент аркуша Excel з таблицею розрахунку основних характеристик СМО різних Міні–АТС
Визначимо величини витрат для кожної Міні-АТС
Таким чином, виконаний аналіз дозволяє упевнено говорити, що найбільш доцільне придбання МІНІ-АТС, що допускає підключення 5 телефонних апаратів.
Завдання для самостійного вирішення
Задача 1
У магазині протягом тижня проводилася реєстрація потоку покупців і часу обслуговування їх продавцями.
Дані реєстрації приведені в таблицях 1 і 2, відповідно.
1. Визначите інтенсивності потоку покупців 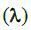 і обслуговування їх продавцями
і обслуговування їх продавцями 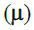 .
.
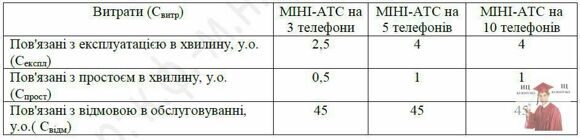
2. Знайдіть кількість продавців, обслуговуючих покупців, робота яких забезпечить найменші витрати роботи магазина (дані по окремих видах витрат приведені в таблиці 3. При цьому в черзі на обслуговування повинні знаходитися не більше 2 покупців.
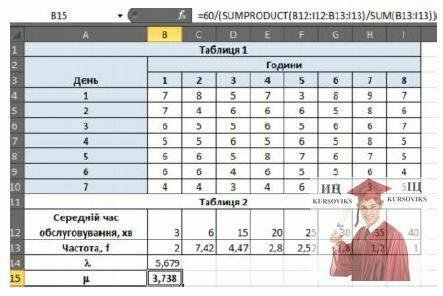
Таблиця 3
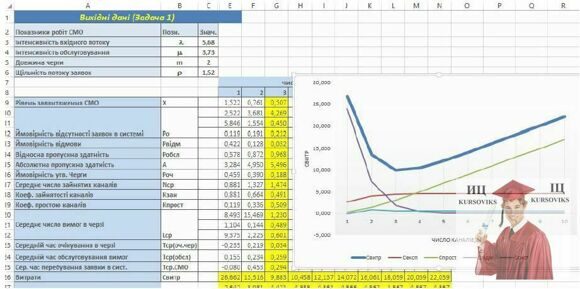
Розв’язок
Виконані розрахунки показують, що при інтенсивності потоку вимог 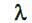 = 5.68 і інтенсивності обслуговування
= 5.68 і інтенсивності обслуговування 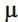 = 3,73 найменша величина витрат може бути досягнута при використанні трьох каналів обслуговування.
= 3,73 найменша величина витрат може бути досягнута при використанні трьох каналів обслуговування.
Задача 2
Ви вирішили відкрити бензозаправну станцію.
Виконані оцінки показують, що в тому місці, де Ви маєте намір її розмістити очікуваний середній інтервал між прибуттям автомобілів на заправку складає 4 хв.
Варіанти устаткування можуть мати час обслуговування автомобіля в межах від 2 до 10 хв.
Визначите:
Зауваження. Для вирішення завдання можуть бути використані процедури «Підбір параметра», «Пошук рішення» і «Сценарії».
1. Яка кількість бензозаправного устаткування з часом обслуговування автомобілів Тобсл = 5 хв має бути придбані з тим, аби відносна пропускна спроможність СМО була не менше 0,85. При цьому, коефіцієнт зайнятості каналів обслуговування має бути 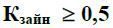 (відповідь n = 2).
(відповідь n = 2).
2. Скільки пунктів обслуговування і якої продуктивності (часу обслуговування) має бути встановлені для того, щоб вартість встановлюваного обладнання була мінімальною Собл = (50* n)/Тобсл
При цьому:
2.1. середній час перебування автомобіля на бензоколонці (СМО) був 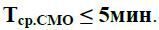 ;
;
2.2. відносна пропускна спроможність СМО має бути 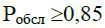 ;
;
2.3. вважаючи, що вартість устаткування обернено пропорційна його продуктивності, а витрати на його придбання і вміст мають бути 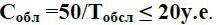
Зауваження
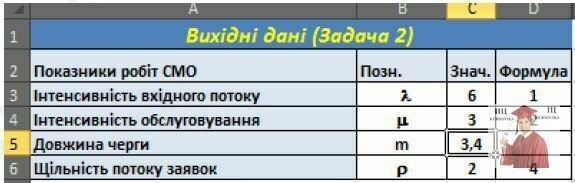
1. Для вирішення завдання вихідні дані зручно представити у вигляді таблиці, подібної показаної на малюнку
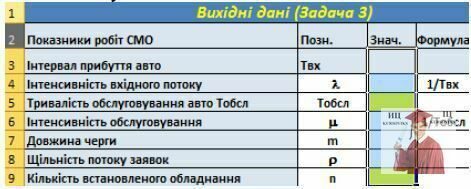
2. При використанні для вирішення завдання процедури «Пошук рішення» або «Підбір параметру» найбільш складним є обчислення виразу.
Одним з варіантів вирішення цієї проблеми може бути запис цього виразу з використанням функції «ЕСЛИ.». Так, наприклад, при розміщенні цієї формули у комірці Е12, створеного раніше шаблону, ця формула може мати вигляд 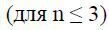 :
:
=IF(C9=1;(C8^0)/FACT(0)+(C8^1)/FACT(1);…
3. Враховуючи те, що частина формул містить нелінійні елементи, при вирішенні задачі як початкові значення Тобсл і n, встановіть
для Тобсл значення близьке до нуля, наприклад Тобсл = 0,01;
для n – мінімальне значення n=1.
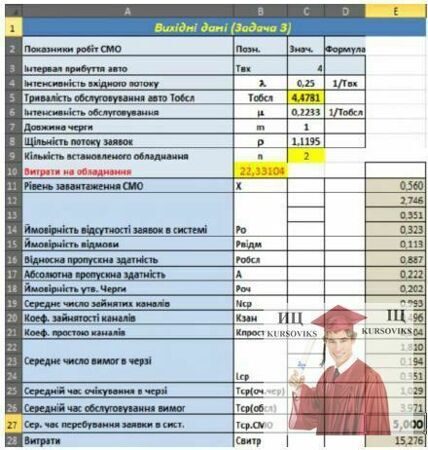
Відповідь
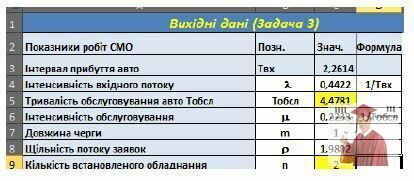
На автозаправці доцільно встановити дві одиниці устаткування з часом обслуговування Тобсл =4,47 мін.
3. Мінімальний інтервал прибуття автомобілів на автозаправку Твх, при якому зберігаються умови стаціонарності роботи СМО (для вирішення використовуйте величину Тобсл, знайдену при рішенні попередньої задачі: Тобсл = 4,47 хв).
Відповідь. При заданому часі обслуговування автомобіля (виходячи із попереднього завдання), мінімальний інтервал їх прибуття на автозаправку складає 2,26 хв (при цьому рівень завантаження СМО =0.99).
Контрольні запитання
1. Як обчислюються основні параметри СМО?
2. Яка умова стаціонарності СМО?
3. Як обчислюється відносна пропускна здатність СМО?
4. Як обчислюється Ймовірність відмови в обслуговуванні вимоги?
5. Як обчислюється рівнем завантаження системи?
6. Як обчислюється Ймовірність обслуговування заявки?
7. Як обчислюється Абсолютна пропускна здатність системи?
8. Як обчислюється Середнє число зайнятих каналів?
9. Як обчислюється Коефіцієнт використання (зайнятості) каналів?
10. Як обчислюється Коефіцієнт простою каналів обслуговування?
11. Як обчислюється Середній час чекання в черзі?
12. Як обчислюється Середній час перебування заявки?
13. Як обчислюється ймовірність утворення черги?