Лабораторна робота №11, Динамічне програмування, Задача про оптимальний шлях

« Назад

Теоретична довідка

Принцип оптимальності Беллмана стверджує, що оптимальне управління системою на кожному кроці не залежить від передісторії процесу, тобто як система досягла поточного стану, а визначається тільки цим станом.

Завдання

Відомо карта поля із скарбами у вигляді матриці розміром 10+n (порядковий номер студента в журналі). Розмір скарба на кожному кроці рівний випадковій величині від n до n+50. Гном знаходиться у верхній лівій точці (1,1) і може рухатись або вниз або вправо. Допоможіть гному зібрати максимальний скарб. Шлях гнома повинен відображатись на матриці скарбів (карта з маршрутом гнома).

Дана задача є різновидом класичної задачі динамічного програмування про вибір траєкторії.

Хід роботи

1. Побудувати вихідну матрицю використовуючи функцію генерування випадкових чисел в заданому діапазоні (від n до n+50).

Рис. 1 - Зразок виконання даного завдання, Excel

2. На основі вихідної матриці побудувати матрицю знаходження максимального скарбу враховуючи що:

максимальний сумарний скарб в даній точці = максимальному значенню із попередніх кроків + значення скарбу в поточній точці, тобто

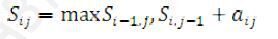
3. Із побудованої матриці можна вказати шлях гнома. Для відображення карти кроків необхідно записати умову проходження за допомогою логічних функцій.

Рис. 2 - Умова проходження шляху гнома за допомогою логічних функцій

де kij – елемент матриці карти кроків;

Sij. – елемент матриці максимальний скарб.

4. Відображення кольором шляху проходження гнома можна забезпечити за допомогою умовного форматування.

Контрольні запитання

1. Які задачі називаються ЗДП?

2. Яка функція називається мультиплікативною?

3. Яка функція називається адитивною?

4. В чому полягає принцип оптимальності Белмана?

5. Як зміниться задачі у випадку її мінімізації?

6. Яка максимальна розмірність матриці в даній задачі допускається?