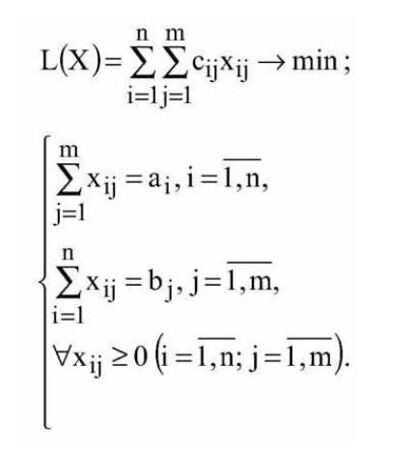Лабораторна робота №2-4, Транспортна задача з фіксованими доплатами, штрафними санкціями

« Назад

1. Запустити програму Microsoft Excel.

2. Вирішити наступні задачі попередньо побудувавши математичну модель до кожного із завдань. Математична модель повинна буди записана на кожному із аркушів відповідно до задач і завдань у вигляді

КОЖНЕ ЗАВДАННЯ ВИКОНУЄТЬСЯ НА ОКРЕМОМУ АРКУШІ

Задача 1

Заводи деякої автомобільної фірми розташовані у містах А, В і С. Основні центри розподілу продукції зосереджені у містах D і E. Обсяги виробництва зазначених трьох заводів дорівнюють 1000, 1300 і 1200 автомобілів щоквартально. Величини квартального попиту в центрах розподілу складають 2300 і 1400 автомобілів відповідно. Вартості перевезення автомобілів залізницею по кожному з можливих маршрутів наведено в табл.

	D	E
А	80	215
В	100	108
С	102	68

До кожного із завдань побудувати Отчет по устойчивости (для задачі 1).

Завдання 1

Побудуйте математичну модель, що дозволяє визначити кількість автомобілів, що перевозяться з кожного заводу в кожен центр розподілу, таким чином, щоб загальні транспортні витрати були мінімальні.

Завдання 2

Побудуйте транспортну модель для вихідних даних задачі за умови, що квартальний попит у пункті розподілу D впав до 1900+n*10 (n –порядковий номер студента в журналі) автомобілів, а випуск на заводі B збільшився до 1500+n*10 автомобілів за квартал.

Завдання 3

Побудуйте математичну модель задачі за умови, що за кожен недопоставлений автомобіль в розподільні центри D і E введені штрафи 200+n*10 і 300+n*10 грн. відповідно. Крім того, поставки з заводу А в розподільний центр E не плануються взагалі.

Задача 2. Транспортна задача з фіксованими доплатами

Є 3 постачальника, які мають обмежену кількість запасів продуктів, і 5 споживачів, у яких є певний попит (замовлення) на ці продукти. Задана матриця вартості перевезення одиниці продукції від певного постачальника до певного споживача, а також за експлуатацію кожної ділянки встановлюється додаткова плата незалежно від відстані та обсягів перевезень, тільки тоді, коли по ньому здійснюється перевезення.

Попит > пропозиції (для парного номера n)

Попит < пропозиції (для непарного номера n)

«Матриця затрат» та «матриця доплат» заповнюють випадковими числами від 1 до 10

Завдання 4. (лінійна задача)

Потрібно знайти такий план перевезень, щоб загальні витрати були мінімальні. Побудуйте математичну модель.

Фактично, це вже не лінійна модель (є функція = ЕСЛИ), але шляхом введення альтернативної змінної (0 або 1) без застосування логічної функції «если» ми залишаємося в класі моделей лінійного програмування.

Рис. 1 - Орієнтовний вигляд аркуша для парного номера студента, Excel

Для збереження лінійності моделі додатково будуємо матрицю обмежень значення якої обчислюються за формулою.

=MIN(Запас_n_постачальника; Попит_n_споживача)*Логічну_змінну.

Врахуйте, що в даній задачі необхідно задати два діапазони підбору значень.

Завдання 5. (нелінійна задача)

На новому аркуші розв’яжіть дану задачу не використовуючи матрицю «Логічна змінна» та «Обмеження» змінивши цільову функцію в таблиці розподіл затрат використовуючи логічний вираз (нелінійність).

У пошуку рішення необхідно вибрати вказати нелінійність моделі.

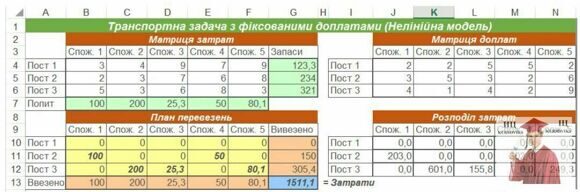
Рис. 2 – Транспортна задача з фіксованими доплатами, Нелінійна модель, Excel

Задача 3

Деякій компанії належать три ферми, де вирощують овочі, призначені для подальшої обробки на двох холодильних заводах компанії. Одним з вирощуваних овочів є боби, які холодильні заводи продають по 200 грн. за 1 т. У Рис. 2 наведені витрати виробництва для кожної ферми і кожного холодильного заводу, максимальні значення врожаю для кожної ферми, прогнозні значення попиту на наступний сезон для кожного заводу. У табл. 1 наведена вартість транспортування бобів.

Таблиця 1

Витрати на виробництво і максимальний урожай бобів

Завдання 6

Побудуйте транспортну модель, яка для ферм і холодильних заводів дозволяє знайти на наступний сезон виробничий план, який гарантує максимальний дохід.

Задача 4

(багатопродуктова модель з незалежними продуктами)

Деяка фірма виробляє автомобілі чотирьох різних марок M1, M2, M3, M4. Завод у місті A виробляє тільки автомобілі марок M3, M4, в місті B - тільки автомобілі марок M1, M2, M4, а в місті C - тільки автомобілі марок M1, M2. Щоквартальні обсяги випуску кожного заводу і величини попиту в кожному пункті розподілу наведено в табл. 2. Побудуйте відповідну модель економічних перевезень. Тарифи перевезень відповідають задачі №1.

Таблиця 2

Обсяги виробництва заводів і попиту пунктів розподілу автомобілів, шт./квартал

Рекомендація. Пункти відправлення в транспортній матриці необхідно вводити відповідно з марками автомобілів, що випускаються кожним заводом, а пункти призначення - відповідно з марками автомобілів, необхідними в кожному пункті розподілу. Пропонований зразок транспортної матриці представлений на рисунку.

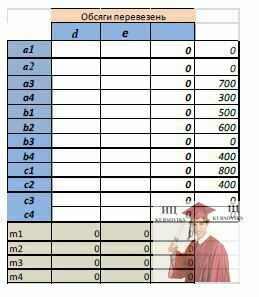
Рис. 3 – Обсяги перевезень, Excel

Задача 5

(багатопродуктова модель із залежними продуктами)

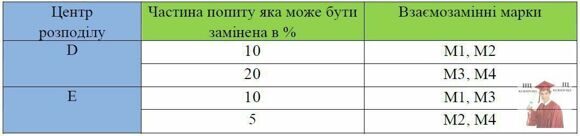
Вихідна умова задачі №4 за умови, що деяку частину попиту на одну з марок можна задовольняти за рахунок іншої відповідно до табл. 3. Побудуйте відповідну модель економічних перевезень.

Таблиця 3

Дані про взаємозамінні марки автомобілів

Рекомендація. Введіть чотири нові пункти призначення, що відповідають комбінаціям (M1 або M2), (M3 або M4), (M1 або M2) і (M2 або M4) (див. табл. 5). Величини потреб нових пунктів призначення визначаються на підставі даних про процентне співвідношення замінних моделей автомобілів.

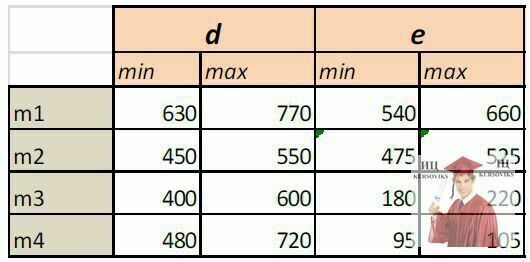
Рис. 4 - Зразок матриці обмежень, Excel

Контрольні запитання

1. До якого типу задач відноситься транспортна задача?

2. Яка особливість транспортних задач?

3. Яка задача називається незбалансованою?

4. Які способи розв’язування незбалансованих задач?