Лабораторна робота №1, Розв’язування систем лінійних алгебраїчних рівнянь в Microsoft Excel

« Назад

Теоретичні відомості

Система m лінійних рівнянь з n невідомими має вигляд:

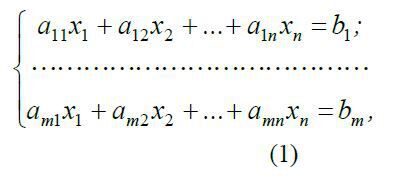
де 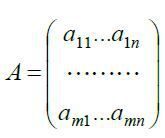 - матриця коефіцієнтів при змінних (матриця системи);

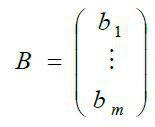- матриця-стовпець (вектор) вільних членів;

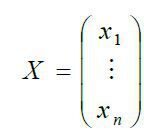матриця-стовпець (вектор) невідомих.

Систему лінійних рівнянь можна записати у матричному вигляді, як

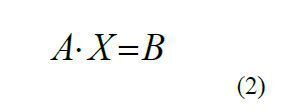
Якщо виконується умова 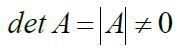, то система має один розв’язок.

При розв’язуванні системи лінійних рівнянь можливі три випадки:

а) m<n.

При m<n, якщо система m лінійних рівнянь з n невідомими є сумісною, то вона не визначена і має нескінченну кількість розв’язків.

б) m=n.

При m=n, система (1) буде мати n лінійних рівнянь з n невідомими. Тоді розв’язок системи можна отримати методом оберненої матриці чи методом Крамера.

Метод оберненої матриці розв’язування системи лінійних рівнянь.

Помножимо ліву і праву частину (2) на обернену матрицю A-1, тоді 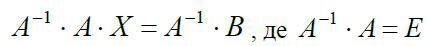(одинична матриця).

Після необхідних перетворень розв`язок лінійної системи методом оберненої матриці матиме вигляд

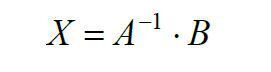(3)

Метод Крамера розв’язування системи лінійних рівнянь.

Цей метод базується на формулах

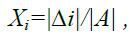(4)

де |∆i| - визначник матриці, одержаної з матриці А заміною і–го стовпця на стовпець вільних членів В;

|A| - визначник матриці А.

в) m>n.

У випадку, якщо m>n і система є сумісною, то матриця А має принаймні m-n лінійно незалежних рядків. Тут розв’язок може бути отримано добором n будь-яких лінійно незалежних рівнянь і застосуванням формули (3).

Однак із застосуванням комп'ютера зручніше використовувати більш загальний підхід - метод найменших квадратів. Для цього обидві частини матричного рівняння системи (2) множимо ліворуч на транспоновану матрицю системи АТ

АТАХ=АТ В

Потім обидві частини рівняння множимо ліворуч на матрицю (АТА)-1. Якщо ця матриця існує, то система визначена. З врахуванням того, що (АТА)-1 *(АТА)=Е, одержуємо

Х=(АТА)-1 *АТВ (5)

Матричне рівняння (5) є розв’язком системи m лінійних рівнянь з n невідомими при m>n.

Завдання

Знайти розв`язок системи лінійних алгебраїчних рівнянь

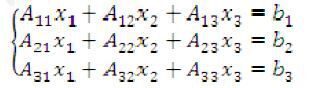
де b1 – порядковий номер стедента в журналі, b2 – день місяця народженння студента, b2 – місяць народження студента, матриця А – довільні числа.

Хід роботи

Розв’язок системи лінійних алгебраїчних рівнянь методом оберненої матриці

1. Запустити програму Microsoft Excel.

2. Переконатись, що система має розв’язок (знайти визначник матриці МОПРЕД).

3. Побудувати електронну таблицю та оформити її наступним чином:

Таблиця 1

Розв’язок системи лінійних алгебраїчних рівнянь методом оберненої матриці

Створити обернену матрицю до матриці А використовуючи функцію – МОБР.

Для роботи з масивами в формулах необхідно натиснути

Ctrl+Shift+Enter.

4. Знайти розв’язок системи використовуючи функцію МУМНОЖ.

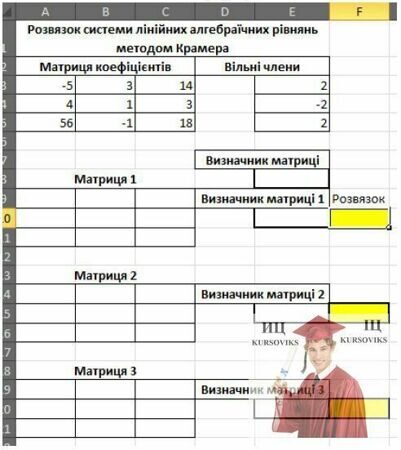
Таблиця 2

Розв’язок системи лінійних алгебраїчних рівнянь методом Крамера

5. Побудувати електронну таблицю на новому аркуші та оформити відповідним чином:

6. Знайти визначник для матриці коефіцієнтів.

7. Знайти визначник для матриці 1, яка одержана із матриці А заміною першого стовпця на стовпець вільних членів.

8. Аналогічно п.7. отримати значення визначника матриці 2 та матриці 3.

9. Знайти розв’язок системи відповідно до (4).

Розв’язок системи лінійних алгебраїчних рівнянь методом найменших квадратів

10. Побудувати електронну таблицю на новому аркуші та оформити відповідним чином:

11. Знайти транспоновану матрицю до матриці коефіцієнтів використовуючи функцію - ТРАНСП.

12. Знайти множення матриці коефіцієнтів на транспоновану матрицю.

13. Знайти обернену матрицю до матриці одержаної в п.12.

14. Знайти множення транспонованої матриці на матрицю вільних членів.

15. Знайти розв’язок системи множенням матриць отриманих в п.13 і п.14.

16. Порівняти розв’язки отримані різними методами.

Контрольні запитання

1. Які три випадки можливі при розв’язуванні системи m лінійних алгебраїчних рівнянь з n невідомими?

2. В чому полягає метод оберненої матриці розв’язування системи лінійних рівнянь?

3. В чому полягає метод Крамера розв’язування системи лінійних рівнянь?

4. В чому полягає метод найменших квадратів розв’язування системи лінійних рівнянь?