Задачі з предмету Системи підтримки та прийняття рішень (СППР) - 30 задач

« Назад

№1

За заданою матрицею гри у чистих стратегіях знайти рішення як рівновагу Неша, вважаючи дії гравців раціональними.

 

№2

За заданою матрицею гри у чистих стратегіях знайти рішення як рівновагу у домінантних стратегіях, вважаючи дії гравців раціональними.

 

№3

За заданою матрицею гри у чистих стратегіях знайти рішення як рівновагу Штакельберга, вважаючи дії гравців раціональними, а лідером – гравця, стратегії і виграші якого задані у стовпчиках.

 

№4

За заданою матрицею гри у чистих стратегіях знайти рішення як рівновагу Неша, вважаючи дії гравців раціональними.

 

№5

За заданою матрицею гри у чистих стратегіях знайти рішення як рівновагу Штакельберга, вважаючи дії гравців раціональними, а лідером – гравця, стратегії і виграші якого задані у стовпчиках.

 

№6

За заданою матрицею гри у чистих стратегіях знайти рішення як рівновагу Штакельберга, вважаючи дії гравців раціональними, а лідером – гравця, стратегії і виграші якого задані у рядках.

 

№7

Дві країни торгують між собою. Вони одночасно вибирають розмір мита р₁ і р₂. Обсяг торгівлі х між країнами залежить (у відносних показниках) від встановленого мита таким чином:

х=1-р₁-р₂.

В даній задачі вважається, що не існує різниці між експортом та імпортом. Знайти величини мита, які відповідають рівновазі Неша.

 

№8

Прийняття рішень в умовах ризику.

Є два інвестиційних проекти. Перший з імовірністю 0,7 забезпечує прибуток 14 млн. грн., однак з імовірністю 0,3 можна втратити 6,5 млн. грн. Для другого проекту з імовірністю 0,8 можна дістати прибуток 9 млн. грн. і з імовірністю 0,2 утратити 6 млн. грн. Який проект вибрати?

 

№9

Знайти найкращу стратегію за критерієм Вальда для наступної матриці платежів гри з природою:

 

№10

Знайти найкращу стратегію за критерієм Севіджа  для наступної матриці платежів гри з природою:

 

№11

Знайти найкращу стратегію за критерієм Гурвіца (коефіцієнт дорівнює 0,3) для наступної матриці платежів гри з природою:

 

№12

Знайти найкращу стратегію за критерієм Гурвіца стосовно матриці ризиків (коефіцієнт дорівнює 0,4) для наступної матриці платежів гри з природою:

 

№13

Керівництво деякої компанії вирішує, створювати для випуску нової продукції розширити існуюче підприємство, створити дочірнє підприємство в іншій країні або продати патент іншій фірмі. Розмір виграшу, який компанія може одержати, залежить від сприятливого чи несприятливого стану ринку (табл.). Ймовірність настання сприятливого стану становить 0,7.

Номер стратегії	Дії компанії	Виграш (грн.) при стані економічного середовища*
		сприятливий	несприятливий
1	Розширення існуючого підприємства	150000	– 110000
2	Створення дочірнього  підприємства	250000	– 200000
3	Продаж патенту	50000	50000

 

№14

На деякій універсальній множині Х={x₁, x₂, x₃, x₄} задано дві нечіткі множини А та В:

A = 0,3/ x1 + 0,2/ x2+0,6/ x3+1/ x4;

B = 0,5/ x1+0,8/ x2+1/ x3+0,4/ x4.

Знайти нечіткі множини C, D та E,  одна з яких є об’єднанням заданих множин, друга – їх перетином, третя – їх різницею.

 

№15

На деякій універсальній множині  альтернатив Х={x₁, x₂, x₃, x₄} задано два нечіткі множини - обмеження С1 та С2

С1 = 0,3/ x₁ + 0,2/ x₂+0,6/ x₃+1/ x₄

С2= 0,5/ x₁+0,8/ x₂+1/ x₃+0,4/ x₄

та нечітка множина - мета

G=0,1/ x₁ +1/ x₂+0,6/ x₃+0,7/ x₄ .

Застосовуючи підхід Беллмана – Заде до даної ситуації невизначеності, знайти рішення щодо вибору найкращої альтернативи.

 

№16

Є два інвестиційних проекти. Перший з імовірністю 0,6 забезпечує прибуток 15 млн грн, однак з імовірністю 0,4 можна втратити 5,5 млн грн. Для другого проекту з імовірністю 0,8 можна дістати прибуток 10 млн грн і з імовірністю 0,2 втратити 6 млн грн. Який проект вибрати?

 

№17

Характеристики інвестиційних проектів представлені у вигляді точок на площині (m, S), де m – середній прибуток, що планують одержати від інвестицій, a S – середньоквадратичне відхилення прибутку. Зробіть вибір між проектами, що позначені точками A, B, C, з погляду  інвестора й обґрунтуйте свій вибір.

 

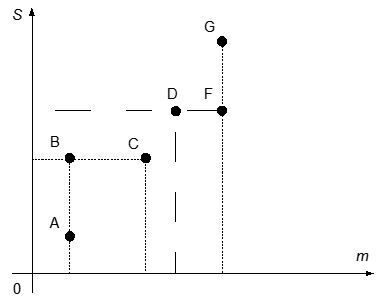
Рисунок 1. Варіанти вибору інвестицій

 

№18

Автомобільний завод одержує реле сигналу повороту від двох постачальників А и В. Якість цих виробів характеризується даними, наведеними в табл. 5.3.

Таблиця Відсоток браку

Відсоток браку	Ймовірність для постачальника
	А	В
1	0,7	0,4
2	0,1	0,3
3	0,09	0,15
4	0,07	0,1
5	0,04	0,05

Повні витрати, пов'язані з ремонтом одного бракованого реле, складають 5 грн.

Реле надходять партіями по 20 000 шт. Оскільки якість виробів у постачальника В гірше, він віддасть всю партію на 500 грн дешевше. Побудуйте дерево рішень. Якого постачальника варто вибрати?

 

№19

При здійсненні багатофазових інвестицій в певного виду підприємницьку діяльність обчислюється величина збитків у вигляді відсотка величини реальних збитків по відношенню до розрахункової суми виручки. Було встановлено, що обчислена таким чином величина збитків підкоряється нормальному закону розподілу з параметрами математичне сподівання та середньоквадратичне відхилення .

Фірма-інвестор встановила для себе такі критерії ризику: .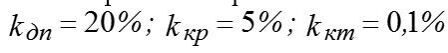

Як вчинити інвестору, якщо керівництво фірми, що прагне отримати інвестиції, вважає реальним показники ризику: ?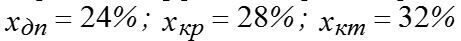

 

№20

Під час досліджень було встановлено: інтегральна функція розподілу випадкової величини, що визначає рівень очікуваних збитків має вигляд:

Суб’єктом керування визначені такі границі допустимого, критичного та катастрофічного ризиків .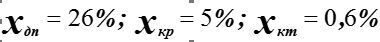

Чи може інвестор вкладати гроші в цю фірму, за умови, що він встановив для себе наступні граничні критерії ризику ?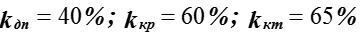

 

№21

Знайти найкращу стратегію за критерієм Гурвіца стосовно матриці ризиків (коефіцієнт дорівнює 0,3) для наступної матриці платежів гри з природою:

 

№22

Залежність доходу І і витрат С від обсягу виробництва х задаються функціями наступного вигляду:

Виробничі потужності дозволяють виробляти до 25 одиниць продукції. Який обсяг виробництва забезпечить максимальний прибуток?

 

№23

Інвестор розглядає чотири інвестиційні операції з випадковими ефективностями, які описуються випадковими величинами E1, E2, E3, E4 з заданими рядами розподілу (табл. 1).

Таблиця 1 – Ряди розподілу до прикладу 8

E1	2	5	8	4		E2	2	3	4	12
р	1/6	1/2	1/6	1/6		р	1/2	1/6	1/6	1/6

E3	3	5	8	10		E4	1	2	4	8
р	1/6	1/6	1/2	1/6		р	1/2	1/6	1/6	1/6

Необхідно визначити, які з цих операцій оптимальні за Парето.

 

№24

Перед відправленням потягу Петрові раптом здалось, що він не вимкнув у квартирі праску. Можна ще встигнути зійти з потягу й виправити помилку, але тоді залишиться невикористаною путівка вартістю 100 000 грн. Якщо ж поїхати, праска, якщо вона дійсно ввімкнена, може викликати пожежу,  ліквідація наслідків якої буде коштувати 1500000 грн. Петро не впевнений, увімкнена праска чи вимкнута. Скласти матрицю наслідків і матрицю жалкувань. Визначити розв’язки, які рекомендовані критеріями Вальда та Севіджа.

 

№25

Дослідити ситуацію прийняття рішень в умовах невизначеності, якщо матриця наслідків має вигляд

 

та відомі ймовірності випадкових величин: 1/2, 1/6, 1/6, 1/6.

Визначити, в якій ситуації досягається максимальний прибуток та мінімальний ризик.

 

№26

Підприємець розмірковує над тим, куди краще вкласти гроші: в кіоск для торгівлі морозивом чи в намет  для торгівлі хлібобулочними виробами.

Вкладення грошей у кіоск з ймовірністю 0,5 забезпечить річний прибуток у розмірі 5000$, з ймовірністю 0,2 - 10000$, з ймовірністю 0,3 - 3000$.

Для намету прогноз стосовно річного прибутку такий: 5500$ з ймовірністю 0,6; 5000$  з ймовірністю 0,3;  6,500$ з ймовірністю  0,1.

В якому випадку математичне сподівання річного прибутку буде більшим, яке рішення обрати?

 

№27

Залежність доходу І і витрат С від обсягу виробництва х задаються функціями наступного вигляду:

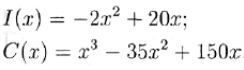
Виробничі потужності дозволяють виробляти до 25 одиниць продукції. Який обсяг виробництва забезпечить максимальний прибуток?

 

№28

Розглядаються два проекти А та В щодо інвестування. Відомі оцінки прогнозованих значень доходу від кожного з цих проектів та відповідні значення ймовірностей. Цифрові дані наведені в таблиці:

Оцінка можливого результату	Прогнозований прибуток, тис. грн		Значення ймовірності
	А	В	А	В
Песимістична	100	51	0,5	0,01
Оптимістична	200	151	0,5	0,99

Визначити математичне сподівання прибутку, дисперсію та середньоквадратичне відхилення. Який проект кращий для інвестування?

 

№29

Надаючи банківські кредити комерційним фірмам, здійснюють прогноз можливих значень збитків та відповідних ймовірностей. Числові дані наведені в таблиці:

Оцінка можливого результату	Прогнозований прибуток, тис. грн		Значення ймовірності
	фірма А	фірма В	фірма А	фірма В
Песимістична	30	70	0,3	0,15
Стримана	6	14	0,5	0,65
Оптимістична	-40	-55	0,2	0,20

Треба визначити математичне сподівання збитків, дисперсію та середньоквадратичне відхилення. Зробити висновки стосовно ризиків.

 

№30

На підставі даних рисунка 1 зробіть вибір між проектами, що позначені точками D, F, G, з погляду інвестора й обґрунтуйте свій вибір.

 

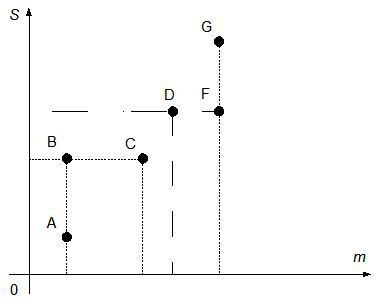
Рисунок 2. Варіанти вибору інвестицій