Лабораторна робота №10, Прийняття рішень в умовах невизначеності та ризику(ігри з природою)

« Назад

Мета роботи: ознайомитися з критеріями пошуку рішень в умовах ризику та невизначеності; навчитися приймати економічні рішення в умовах ризику на підставі теорії ігор та критеріїв пошуку рішень в умовах ризику та невизначеності, з використанням електронних таблиць.

Відмінна риса гри з природою полягає в тому, що в ній свідомо діє тільки один з учасників, що у більшості випадків називається першим гравцем. Другий гравець (природа) свідомо проти першого гравця не діє, а виступає як такий партнер по грі, що не має конкретної мети і випадковим чином визначає чергові "ходи". Тому термін "природа" характеризує деяку об'єктивну дійсність, що не слід розуміти буквально, хоча цілком можуть зустрітися ситуації, у яких другим "гравцем" дійсно може бути природа (наприклад, обставини, пов'язані з погодними умовами або з природними стихійними силами).

Розглянемо організацію та аналітичне представлення гри з природою. Нехай перший гравець має m можливих стратегій: 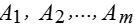, а в природи є n можливих станів (стратегій): 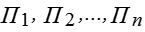, тоді умови гри з природою задаються матрицею А виграшів гравця 1:

 

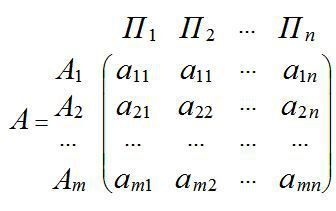
Можливий також інший спосіб завдання матриці гри з природою: не у вигляді матриці виграшів, а у вигляді так званої матриці ризиків 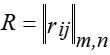або матриці втрачених можливостей. Ризиком  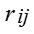гравця при використанні ним стратегії  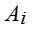та при стані середовища  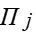будемо називати різницю між виграшем, який гравець одержав би, якби він знав, що станом середовища буде 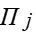, і виграшем, що гравець отримає, не маючи цієї інформації. Знаючи стан природи (стратегію) 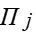, гравець вибирає ту стратегію, за якою його виграш максимальний, тобто

  (4.2)

У випадках, коли невизначеність пов’язана з повною відсутністю інформації про ймовірності станів середовища (природи) для визначення найкращих рішень використовуються наступні критерії: максимаксу, Вальда, Севіджа, Гурвиця та Лапласа.

Критерій максимаксу. З його допомогою визначається стратегія, що максимізує максимальні виграші для кожного стану природи. Це критерій крайнього оптимізму. Найкращим визнається Розв’язання, при якому досягається максимальний виграш, рівний

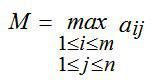  (4.3)

 

Максимінний критерій Вальда. З позицій даного критерію природа розглядається як агресивно налаштований і свідомо діючий супротивник. Вибирається Розв’язання , для якого досягається значення

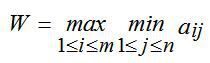  (4.4)

 

Критерій мінімаксного ризику Севіджа. Вибір стратегії аналогічний вибору стратегії за принципом Вальда з тією відмінністю, що гравець керується не матрицею виграшів А, а матрицею ризиків R:

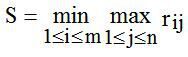(4.5)

 

Критерій песимізму-оптимізму Гурвиця. Цей критерій при виборі рішення рекомендує керуватися деяким середнім результатом, що характеризує стан між крайнім песимізмом і невтримним оптимізмом. Відповідно до цього критерію стратегія в матриці А вибирається згідно зі значенням

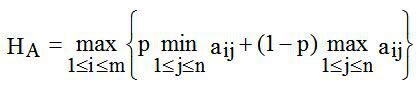  (4.6)

 

де р – коефіцієнт песимізму .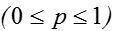

При p = 0 критерій Гурвиця збігається з максимаксним критерієм, а при р = 1 – із критерієм Вальда.

Стосовно матриці ризиків R критерій песимізму-оптимізму Гурвіца має вигляд

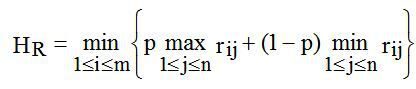  (4.7)

 

При р = 0 вибір стратегії гравця 1 здійснюється за умовою найменшого з усіх можливих ризиків   ; при р = 1 – по критерію мінімаксного ризику Севіджа.

На закінчення наведемо результати застосування розглянутих вище критеріїв на прикладі наступної матриці виграшів:

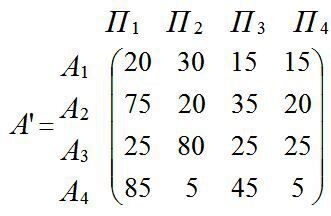  (4.8)

Для гравця 1 кращими є стратегії:

за критерієм Вальда – А3;

за критерієм Севіджа – А2 та А3

за критерієм Гурвиця (при р = 0,6) – А3;

за критерієм максимаксу – А4.

Оскільки стратегія А3 фігурує як оптимальна за трьома критеріями вибору з чотирьох, ступінь її надійності можна визнати досить високим, для того щоб рекомендувати цю стратегію до практичного застосування.

Прийняття рішень в умовах ризику. Методи прийняття рішень в умовах ризику розробляються та обґрунтовуються у рамках так званої теорії статистичних рішень. При цьому у випадку "доброякісної", або стохастичної, невизначеності, коли станам природи поставлені у відповідність ймовірності, задані експертно або обчислені, Розв’язання , як правило, приймається на підставі критерію максимуму очікуваного середнього виграшу або мінімуму очікуваного середнього ризику.

Якщо для деякої гри з природою, що задається платіжною матрицею 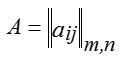, стратегіям природи  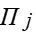відповідають імовірності p_j, то кращою стратегією гравця 1 буде та, що забезпечує йому максимальний середній виграш, тобто

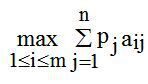(4.9)

Стосовно матриці ризиків (матриці втрачених вигод) кращою буде та стратегія гравця, що забезпечує йому мінімальний середній ризик:

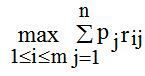(4.10)

 

4.2. Розв’язання прикладу у середовищі електронних таблиць

Розглянемо вибір стратегій першого ігрока за допомогою наведених критеріїв прийняття рішень в умовах ризику та невизначеності.

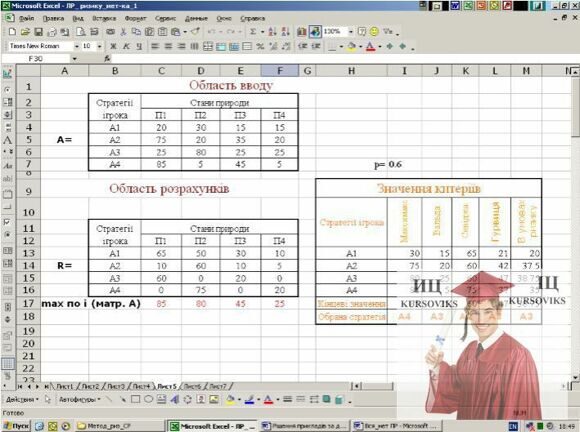
Заповнення області вводу. В області вводу розміщуємо тільки матрицю виграшів –  (4.8), всі інші дані розраховуватимуться на її підставі. Таблицю з даними розташуємо у діапазоні B7:F7, а числові значення виграшів у діапазоні С4:F7 (рис. 1).

Рисунок. 1 – Вибір стратегії у грі з природою

Зауваження. Клітинки В2, В3 об’єднуємо і ставимо прапорець Переносить по слогам.

Зауваження. Для заповнення областей В4:В7 та С3: F3 достатньо ввести дані у першу клітинку, наприклад, у В4, а потім заповнити решту діапазону за допомогою маркеру заповнення.

Текстову інформацію, що пояснює початкові данні вводимо відповідно до рисунку 4.1 та окреслюємо границі таблиці.

 

Заповнення області розрахунків. Розглянуті критерії розраховуються на підставі двох матриць: матриці виграшів А, та матриці втрат R. Тому спочатку у області розрахунків, у діапазоні В11:F16 будуємо матрицю R, користуючись формулою (4.2). Для цього потрібно знайти максимальне значення у кожному стовпчику. Ці значення знаходимо за допомогою функції MAX() (категорія Статистические).

Наприклад, максимальне значення для першого стовпця П1 розміщуємо у клітинці С17: за допомогою майстра функцій викликаємо діалогове вікно функції МАX(), у першому полі вводу якого вказуємо діапазон С4:С7 та натискаємо ОК. Максимальні значення для інших стовпців розташовуємо у діапазоні D17:F17 за допомогою маркеру заповнення.

Формування матриці втрат R складається з виконання таких пунктів:

1) виділяємо діапазон C13:F16;

2) у рядок вводу та редагування формул вносимо формулу C$17-C4;

3) натискаємо Ctrl+Shift+Enter.

Таким чином заповнюємо відразу всю потрібну область. Зверніть увагу, що посилання на клітинку С17 має змішаний вид, оскільки максимальні значення розташовані в одному рядку, номер рядка незмінний, а тому посилання на рядок є абсолютним.

Після того, як сформовано матрицю втрат перейдемо до розрахунку значень критеріїв прийняття рішень. Таблиця значень критеріїв містить: значення за критерієм по кожній стратегій ігрока, кінцеве значення критерію та номер обраної за даним критерієм стратегії. Таблицю розташовуваємо у діапазоні Н9:М18.

Перший з розглянутих критеріїв – критерій максимаксу (4.3). Згідно з цим критерієм для кожної стратегії потрібно знайти найкраще значення у матриці виграшів (тобто найбільше), та з отриманих результатів обрати найбільше значення. Значення критерію максимаксу для кожної стратегії вносимо у діапазон І13:І16, застосовуючи прийом заповнення діапазону, який ми використовували раніше для формування матриці втрат. Діапазон заповнюється функцією МАX(), аргументом якої в даному випадку є діапазон C4:F4 – тобто рядок матриці виграшів, що відповідає першій стратегії ігрока. Кінцеве значення цього критерію знаходимо за допомогою тієї ж функції з аргументом І13:І16 у клітинці І17.

Наступний критерій – максимінний критерій Вальда (4.4), за яким потрібно спочатку знайти найгірше значення у матриці виграшів (тобто найменше), а потім з отриманих результатів обрати найбільше значення. Значення критерію Вальда для кожної стратегії вносимо у діапазон J13:J16, що заповнюється функцією МIN(), з аргументом C4:F4. Для визначення кінцевого значення критерію Вальда вносимо у клітинку J17 формулу, що визначає максимальне значення у щойно заповненому діапазоні – J13:J16.

Пошук стратегії за критерієм Севіджа (4.5) відбувається аналогічно пошуку за критерієм Вальда, але на підставі матриці втрат. Проміжні значення критерію Севіджа вносимо у діапазон К13:К16, заповнюючи його функцією МАX(), з аргументом C13:F13 – шукаємо найгірші значення для кожної стратегії. Кінцеве значення знаходимо за допомогою функції МIN() з аргументом К13:К16 у клітинці К17 – з найгірших варіантів обираємо найкращій.

Для пошуку стратегії за критерієм песимізму-оптимізму Гурвиця потрібна додаткова інформація, а само – значення коефіцієнта песимізму р. Внесемо його у клітинку І7 області вводу. Далі, відповідно до розглянутої формули критерію Гурвиця (4.6), заповнюємо діапазон L13:L16 формулою $I$7*J13+(1-$I$7)*I13. В наведеній формулі J13 та I13 – посилання на клітинки, що містять відповідно найгірше (мінімальне) та найкраще (максимальне) значення виграшу для кожної стратегії, $I$7 – абсолютне посилання на клітинку, що містить значення коефіцієнта песимізму р. У клітинці L17 формуємо кінцеве значення за критерієм песимізму-оптимізму Гурвиця, тобто обираємо максимальне значення з діапазону L13:L16.

В умовах ризику рішення приймаються з урахуванням ймовірностей виникнення кожного зі станів природи (4.9), (4.10). Значення ймовірностей невідомі, тому припустимо, що вони однакові та дорівнюють  (найскладніший випадок з точки зору прийняття Розв’язання). Діапазон М13:М16 заповнимо значеннями очікуваного середнього виграшу для кожної стратегії: для цього внесемо в нього формулу C4*(1/4)+D4*(1/4)+E4*(1/4)+F4*(1/4) (або формулу (C4+D4+E4+F4)*(1/4)).

Зауваження. Замість значення (1/4) можна ввести посилання на клітинку Області вводу, що містить відповідне значення, або ж на відповідну клітинку рядку, що містить значення ймовірностей кожного зі станів природи.

Кінцевий результат за критерієм буде дорівнювати максимальному зі знайдених значень і знаходитиметься у клітинці М17 (МАX(M13:M16)). Найкращу за цим критерієм стратегію можна шукати також використовуючи матрицю втрат, але в цьому випадку треба шукати стратегію з найменшим значенням очікуваного середнього ризику.

Мета розв’язання даного прикладу – визначити стратегії найкращі за кожним з критеріїв, тому в останньому рядку таблиці потрібно навести номер цих стратегій (А1, А2, А3 або А4). Для цього використаємо функцію IF(), за допомогою якої порівняємо кінцеве значення кожного критерію з діапазону І7:М17 зі значеннями у відповідному діапазоні проміжних значень для кожної стратегії (наприклад з діапазону І13:І16 для критерію максимаксу), та у клітинку нижче занесемо значення тієї стратегії, значення якої дорівнює кінцевому значенню за критерієм. Остаточну відповідь сформуємо у діапазоні І18:М18, для чого заповнимо її формулою = IF(I17=I13,$H$13,IF(I17=I14,$H$14,IF(I17=I15,$H$15,$H$16))).

Висновки

Після автоматизації процесу пошуку рішень в умовах ризику та невизначеності для запропонованої матриці виграшів, було отримано наступні результати:

- за критерієм максимаксу найкращою стратегією є А4;

- за критерієм Вальда – А3;

- за критерієм Севіджа – А2 ;

- за критерієм Гурвіца (при р = 0,6) – А3;

- в умовах ризику – А3.

Розбіжність результатів за деякими з критеріїв свідчить про те, що вони відповідають різним ставленням ОПР до ризику, починаючи з найоптимістичнішого (критерій максиміну). Однак, за більшістю критеріїв найкращою є А3, тому вона може бути визнана оптимальною.

Запропонована автоматизація моделі може використовуватися для матриці виграшів розміром 4х4. Тому потрібно доопрацювання даного методу автоматизації з метою універсалізацій його з точки зору розмірності матриці виграшів. Необхідними є також корективи, що дозволять враховувати випадки, коли кілька стратегій одночасно мають найкращі результати за одним критерієм (наприклад, за критерієм Севіджа найменший результат 60 мають друга та третя стратегії).

Для перевірки правильності виконання роботи треба:

1. Порівняти отримані результати із зображеними на рис.4.1.

2. Перевірити, чи відповідно змінюються результати при внесенні інших значень в матрицю виграшів.

3. Усно пояснити використання посилань у функції IF().

4. Пояснити метод заповнення діапазонів C13:F13 та I18:M18.

 

Завдання для самостійного розв’язання

Задача 4.1. Знайти найкращі стратегії за критеріями: максимаксу, Вальда, Севіджа, Гурвіца (коефіцієнт дорівнює 0,2) , Гурвіца стосовно матриці ризиків (коефіцієнт дорівнює 0,4) для наступної матриці платежів ігри з природою:

Розв’язання задачі реалізувати за допомогою електронних таблиць.

 

Задача 4.2. Дана матриця ігри з природою в умовах цілковитої невизначеності:

Потрібно: проаналізувати оптимальні стратегії першого гравця, використовуючи критерії песимизму-оптимізму Гурвиця стосовно матриці платежів та матриці ризиків при коефіцієнті песимізму р = 0; 0,5; 1; встановити, яку роль відіграють стратегії ОПР при р = 0,5.

Розв’язання задачі реалізувати за допомогою електронних таблиць.

 

Задача 4.3. Магазин "Молоко" продає вроздріб молочні продукти. Директор магазину повинен визначити, скільки бідонів сметани варто закупити у виробника для торгівлі протягом тижня. Імовірності того, що попит на сметану протягом тижня буде 7, 8, 9 або 10 бідонів, рівні відповідно 0,2; 0,2; 0,5 і 0,1. Покупка одного бідона сметани коштує для магазину 70 грн, а продається сметана за ціною 110 грн за бідон. Якщо сметана не продається протягом тижня, вона псується, і магазин несе збитки. Скільки бідонів сметани бажано закуповувати для продажу?

Розв’язання задачі реалізувати за допомогою електронних таблиць.

 

Задача 4.4. Необхідно оцінити один з трьох програмних продуктів а_і, що розробляються для боротьби з одним з чотирьох типів програмних впливів k_j.

Матриця ефективності наведена у таблиці.

аі	kj
	k1	k2	k3	k4
a1	0,1	0,5	0,1	0,2
a2	0,2	0,3	0,2	0,4
a3	0,1	0,4	0,4	0,3

Який з програмних продуктів слід розробляти?

Розв’язання задачі реалізувати за допомогою електронних таблиць.

 

Перелік питань

1. Назвіть критерії пошуку рішень в умовах ризику та невизначеності.

2. Наведіть сутність критеріїв пошуку рішень в умовах ризику та невизначеності.

3. За якими формулами обчислюються критерії пошуку рішень в умовах ризику та невизначеності?

4. Чим відрізняються ситуації ризику від ситуацій невизначеності?

5. У яких випадках доцільно використовувати ті або інші критерії пошуку рішень в умовах ризику та невизначеності?