Наукова стаття Економіко-математичне моделювання портфеля комерційного банку

« Назад

Формування й успішна діяльність банківської системи, входження вітчизняних банків у міжнародний бізнес значною мірою залежить від кваліфікації, знань та умінь банківських працівників управляти фінансами, вдало вирішувати, впливати на ефективність діяльності банківської установи. Тому для успішної діяльності банківських і небанківських установ, особливо в час економічного спаду, моделювання структури портфеля є вкрай необхідним.

Аналізу та методам розрахунку оптимального портфеля, найбільш вигідному плану розподілу і перерозподілу інвестицій присвячено велику кількість досліджень. Економіко-математична модель задачі вибору оптимальної структури портфеля вперше запропоновано Г. Марковіцем. Інший відомий американський вчений-економіст Д. Тобін узагальнив її, показавши, що оптимальна структура портфеля цінних паперів не залежить від схильності (несхильності) інвестора до ризику [2].

Вітчизняні вчені також активно розвивали теорію управління інвестиційними портфелями. Так, Б. Луців запропонував підхід до моделювання банківської інтегрованої системи формування і управління інвестиційним портфелем. Б. Пшик розглянув сучасні методи прийняття управлінських рішень. Л. Дума та М. Бурда розглядають випадок оптимізації портфеля цінних паперів з невідомими середніми. Проте і на сьогодні серед вітчизняних вчених немає єдиної думки щодо моделювання оптимального інвестиційного портфеля комерційного банку [3].

На нашу думку, на даний час є надзвичайно важливим питанням побудова оптимальної структури портфеля комерційного банку з використанням семіковаріації замість коваріаційної характеристики як міри ризику в класичній задачі Марковіца, що дає змогу уникнути одного з недоліків цієї моделі – припущення, що коливання норми доходу портфеля в обидві сторони від сподіваної величини однаково небажані.

Ми вважаємо, що той банк, що є найбільшим учасником фондового ринку на рівні держави, рано чи пізно стає найбільшим банком з вітчизняним капіталом та має найбільший кредитно-інвестиційний портфель.

Вітлінський В.В. вважає, що формально економіко-математичну модель класичної моделі Марковіца можна подати у вигляді такої двокритеріальної задачі вибору оптимального рішення:

де - доходність, -ризик, х_і – частка капіталу, вкладеного в і – у групу активів, -очікувана доходність і – ої групи активів, - коваріація між доходностями груп активів i та j групи. [1]

Проте ця модель має велику кількість недоліків, а неокласична теорія портфеля намагається відшукати шляхи її усунення. Наприклад, у класичній теорії використовується гіпотеза, що коливання норми доходу портфеля в обидві сторони від сподіваної величини однаково небажані. Проте, звісно, ризик пов'язаний з несприятливими ситуаціями, і для його оцінювання достатньо брати до уваги лише несприятливі відхилення від очікуваної величини, а не всі відхилення. Тому в неокласичній теорії портфеля за міру ризику пропонується взяти семі варіацію, яка для дискретної випадкової величини Х обчислюється так:

 

де семіковаріація характеристика випадкових величин  та  вираховується за формулою:

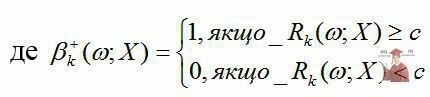
де  - індикатор сприятливих відхилень [5-6].

Отже, для формування оптимізаційної структури портфеля за групами активів використано модифіковану задачу Марковіца з використанням семі варіації як міри ризику.

Розрахунок доходності для цінних паперів визначався таким чином:

 

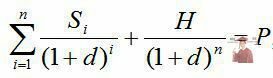
де S_i – очікуваний потік відсоткових виплат за цінним папером в і – й період; n – кількість періодів, протягом яких цінний папір приносить дохід; Н – номінальна вартість цінного паперу; Р – поточна ринкова вартість цінного паперу; d – дохідність цінного паперу до моменту погашення (невідома величина). [ 4 ]

Досить ефективним для відображення залежності доходів від ризику за оптимальної структури портфеля є побудова графіка (співвідношення ризик-дохід). За даними графіка можна сказати чи є розподіл близьким до оптимального, чи ні.

На нашу думку, використання семіваріації у моделі Марковіца, як міри ризику, дає змогу уникнути одного з недоліків класичної теорії – припущення, що коливання норми доходу портфеля в обидві сторони від сподіваної величини однаково не бажані.

Це дає можливість у формуванні більш оптимальної структури інвестиційного портфелю банку, що дозволить підвищити його дохідність і знизити рівень портфельного ризику.

Отже, класична модель Марковіца є недосить ефективною і має певні недоліки, більш ефективно використовувати семі варіацію у даній моделі.