Лабораторна робота №3, Оцінка ризиків за допомогою дерева рішень, Варіант №14

« Назад

Мета роботи

Моделювання задачі вибору рішень в умовах ризику за допомогою дерева рішень. Побудова дерева рішень.

Теоретичні відомості

У випадку невеликого числа змінних і можливих сценаріїв розвитку проекту для аналізу ризиків можна також скористатися методом дерева рішень. Воно дає змогу розчленувати велику, складну проблему на серію дрібніших проблем.

Цей метод передбачає графічну побудову варіантів вкладених рішень. Гілкам дерева ставлять у відповідність суб’єктивні й об’єктивні оцінки можливих подій. Йдучи вздовж побудованих гілок, оцінюють кожен шлях, як правило, на основі вірогідностей, і з усіх можливих оцінок вибирають варіант дій з найменшою вірогідністю. При цьому кількісну оцінку одержує кожен варіант.

Дерево рішень – це графічний підхід до аналізу рішень в умовах невизначеності. У процесі побудови дерева використовується два види гілок: гілка рішень і гілка подій. Гілка рішень передбачає прийняття того чи іншого рішення. Вона позначається у вигляді вершини з гілками (рішеннями), що відходять від неї (див рис.3.1).

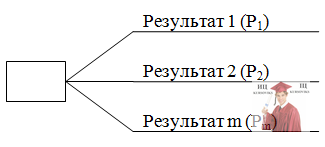
Рис. 3.1 - Принциповий вид дерева рішень

Гілку подій малюють тоді, коли зовнішні фактори визначають, яка з можливих подій відбудеться. Кожна гілка відображає можливий результат, а число P_i, що асоціюється з кожною гілкою, являє собою вірогідність, з якою ця подія відбувається.

Перевага такого методу — у його наочності. У результаті побудови дерева рішень визначається імовірність кожного сценарію розвитку проекту, ефективність за кожним сценарієм, а також інтегральна ефективність проекту. Позитивна величина показника ефективності проекту вказує на прийнятний ступінь ризиків, пов'язаних із здійсненням проекту.

Процес прийняття рішень за допомогою дерева рішень, у загальному випадку передбачає виконання таких п'яти етапів.

Етап 1. Формулювання задачі. Насамперед  необхідно відкинути не стосовні до проблеми фактори, а серед багатьох, що залишилися, виділити суттєві і несуттєві. Це дозволить привести описання задачі прийняття рішення до форми, що піддається аналізу.

Повинні виконуватись такі основні процедури:

- визначення можливостей збору інформації для експериментування і реальних дій;

- складання переліку подій, які з певною імовірністю можуть відбутися;

- встановлення тимчасового порядку розташування подій, в кінцевому результаті яких міститься корисна і доступна інформація, а також тих послідовних дій, які можна застосувати.

Етап 2. Побудова дерева рішень.

Етап 3. Оцінка імовірностей станів середовища, тобто зіставлення шансів виникнення кожної конкретної події. Зазначимо, що вказані імовірності визначаються або на підставі наявної статистики, або експертним шляхом.

Етап 4. Встановлення виграшів (чи програшів, як виграшів зі знаком мінус) для кожної можливої комбінації альтернатив (дій) і станів середовища.

Етап 5. Рішення задачі.

Перш, ніж продемонструвати процедуру застосування дерева рішень, введемо ряд визначень. Залежно від відношення до ризику вирішення задачі може виконуватися з позицій так званих об'єктивістів і суб'єктивістів. Пояснимо ці поняття на наступному прикладі. Проводиться лотерея: за 10 г.о.(грошових одиниць) – (вартість лотерейного квитка) – гравець з рівною імовірністю р=0,5 може нічого не виграти або виграти 100 г.о. Один індивід пошкодує і 10 г.о. за право участі в такій лотереї, тобто просто не купить лотерейний квиток, інший готовий заплатити за лотерейний квиток 50 г.о., а третій заплатить навіть 60 г.о. за можливість одержати 100 г.о. (у третього гравця ситуація складається так, що, тільки маючи 100 г.о., він може досягти своєї мети, тому можлива втрата останніх 60 г.о. для нього не змінює ситуацію).

Безумовним грошовим еквівалентом (БГЕ) гри називається максимальна сума грошей, яку особа, що приймає рішення, готова заплатити за участь у грі (лотереї), чи, що аналогічно, та мінімальна сума грошей, за яку вона готова відмовитися від гри. Кожен індивід має свій БГЕ.

Індивіда, для якого БГЕ збігається з очікуваною грошовою оцінкою (ОГО) гри, тобто із середнім виграшем у грі (лотереї), умовно називають об'єктивістом, у іншому випадку - суб'єктивістом. Очікувана грошова оцінка розраховується, як сума добутків розмірів виграшів на імовірність цих виграшів. Наприклад, для нашої лотереї

ОГО = 0,5x0 + 0,5x100 = 50 г.о.

Якщо суб'єктивіст схильний до ризику, то його БГЕ>ОГО. Якщо він не схильний, то БГЕ<ОГО. Припустимо, що рішення приймаються з позиції об'єктивіста.

Хід роботи

Керівництво підприємства має вирішити, створювати для випуску нової продукції велике виробництво, мале підприємство чи продати патент. Розмір виграшу в г.о. (грошових одиницях), що може одержати підприємство, залежить від сприятливих чи несприятливих умов, що склалися на ринку, оцінюваних рівновірогідно, тобто з вірогідністями 0,5 (див таблицю).

Таблиця

№ варіанта	Дії фірми	Виграш фірми в г.о. залежно від умов ринку
		сприятливі	несприятливі
1	Створення великого виробництва	А1	В1
2	Створення малого підприємства	А2	В2
3	Продаж патенту	А3	В3

Потрібно вибрати оптимальний варіант для фірми.