Лабораторная работа №5, Парная регрессия и корреляция, MS Excel

« Назад

По территориям региона приводятся данные:

Таблица 1

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, ден.ед., x	Среднедневная заработная плата, ден.ед., y
1	85	139
2	86	148
3	87	142
4	79	154
5	106	164
6	113	195
7	67	139
8	98	164
9	79	152
10	87	162
11	86	152
12	117	173

 

Требуется:

1. Построить линейное уравнение парной регрессии y по x.

Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 2.

Таблица 2

№	x	y	y*x	x2	y2				ki
1	2	3	4	5	6	7	8	9	10
1	85	139	11815	7225	19321	151,80	-12,80	163,93	9,21
2	86	148	12728	7396	21904	152,69	-4,69	22,04	3,17
3	87	142	12354	7569	20164	153,59	-11,59	134,21	8,16
4	79	154	12166	6241	23716	146,46	7,54	56,88	4,90
5	106	164	17384	11236	26896	170,51	-6,51	42,40	3,97
6	113	195	22035	12769	38025	176,75	18,25	333,16	9,36
7	67	139	9313	4489	19321	135,77	3,23	10,45	2,33
8	98	164	16072	9604	26896	163,38	0,62	0,38	0,38
9	79	152	12008	6241	23104	146,46	5,54	30,71	3,65
10	87	162	14094	7569	26244	153,59	8,41	70,81	5,19
11	86	152	13072	7396	23104	152,69	-0,69	0,48	0,46
12	117	173	20241	13689	29929	180,31	-7,31	53,45	4,23
Итого	1090	1884	173282	101424	298624	1884	0,00	918,89	54,99
Среднее значение	90,83	157	14440,17	8452	24885,33	157	–	76,57	4,58
	14,19	15,37	–	–	–	–	–		–
	201,31	236,33	–	–	–	–	–		–

По формулам находим параметры регрессии

Получено уравнение регрессии:

.

Параметр регрессии позволяет сделать вывод, что с увеличением среднедушевого прожиточного минимума на 1 ден.ед. среднедневная заработная плата возрастает в среднем на 0,89 ден.ед.

После нахождения уравнения регрессии заполняем столбцы 7 – 10 таблицы 2.

2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.

Тесноту линейной связи оценит коэффициент корреляции:

Т.к. значение коэффициента корреляции больше 0,7, то это говорит о наличии весьма тесной линейной связи между признаками.

Коэффициент детерминации:

Это означает, что 67,6% вариации заработной платы (y) объясняется вариацией фактора x – среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации:

Качество построенной модели оценивается как хорошее, так как 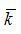 не превышает 10%.

3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью -критерия Фишера и t-критерия Стьюдента.

Оценку статистической значимости уравнения регрессии в целом проведем с помощью F-критерия Фишера. Фактическое значение F-критерия по формуле составит

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы k₁=1 и k₂=12-2=10 составляет F_табл=4,96. Так как , то уравнение регрессии признается статистически значимым.

Оценку статистической значимости параметров регрессии и корреляции проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из параметров.

Табличное значение t-критерия для числа степеней свободы df=n-2=12-2=10 и уровня значимости 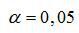 составит t_табл=2,23.

Определим стандартные ошибки   (остаточная дисперсия на одну степень свободы

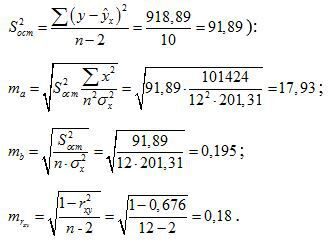
Тогда

Фактические значения t-статистики превосходят табличное значение:

Поэтому параметры a, b и r_xy не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительные интервалы для параметров регрессии a и b. Для этого определим предельную ошибку для каждого показателя:

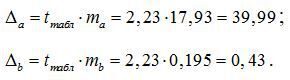
Доверительные интервалы

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью  параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.

4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от  среднего уровня.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:  ден.ед., тогда индивидуальное прогнозное значение заработной платы составит:  ден.ед.

5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Ошибка прогноза составит:

Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

Доверительный интервал прогноза:

Выполненный прогноз среднемесячной заработной платы является надежным () и находится в пределах от 140,16 ден.ед. до 185,0 ден.ед.

6. На одном графике отложить исходные данные и теоретическую прямую.

7. Проверить вычисления в MS Excel.

Выбираем Сервис®Анализ данных®Регрессия. Заполняем диалоговое окно ввода данных и параметров вывода. Получаем следующие результаты:

Откуда выписываем.

Уравнение регрессии:

Коэффициент корреляции:

Коэффициент детерминации:

Фактическое значение F-критерия Фишера:

Остаточная дисперсия на одну степень свободы:

Корень квадратный из остаточной дисперсии (стандартная ошибка):

Стандартные ошибки для параметров регрессии:

Фактические значения t-критерия Стьюдента:

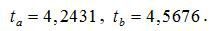
Доверительные интервалы:

Как видим, найдены все рассмотренные выше параметры и характеристики уравнения регрессии, за исключением средней ошибки аппроксимации (значение t-критерия Стьюдента для коэффициента корреляции совпадает с t_b). Результаты «ручного счета» от машинного отличаются незначительно (отличия связаны с ошибками округления).