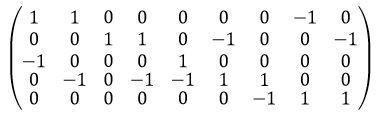Контрольная работа с курса Компьютерная математика - Вариант №6

« Назад

Задание 1

Упростить выражение с множествами:

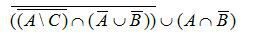
Решение:

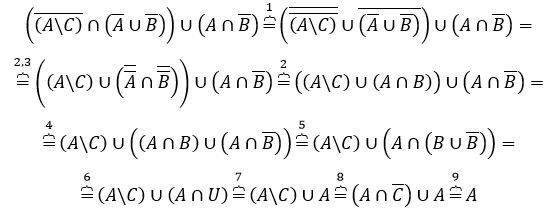
Основные равносильности:

 

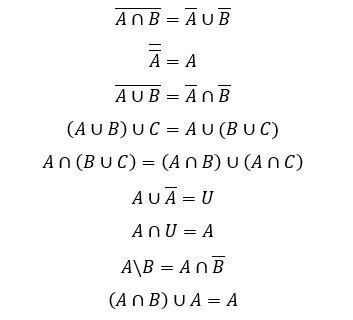
Задание 2

Даны множества A и B. Найти их декартово произведение:

A={2, 4, 7, 8}, B = {1, 4, 5}

Решение:

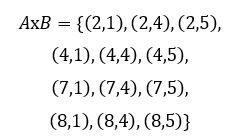
Задание 3

Дано множество A. Задать на нем указанное отношение:

A = {2, 3, 5, 8, 10}, делиться без остатка

Решение:

Здесь A – область задания отношения.

Зададим отношение перечислением

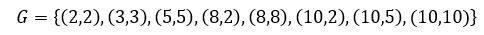
Здесь, например, пара (8, 2) указана, так как число 8 делится на число 2 без остатка. Другими словами, число 8 находится в отношении «делиться без остатка» с числом 2. Пара (2, 8) отсутствует, так как число 2 не делится на число 8 без остатка.

Зададим отношение описанием свойств

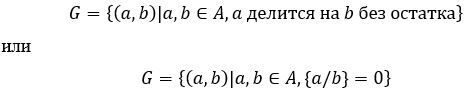
здесь {a/b} - обозначение дробной части деления a на b.

Зададим отношение матричным способом

Для этого строится матрица (обозначим ее, например, R) размерностью n×n, где n – количество элементов в области задания.

Значения элементов матрицы R определяются следующим образом:

- R_ij = 1, если элемент  из области задания находится в заданном отношении с элементом  из области задания, или, другими словами, если

- R_ij = 0, если элемент  не находится в заданном отношении с элементом a_j, т.е.  .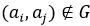

В рассматриваемой задаче матричное задание отношения будет следующим:

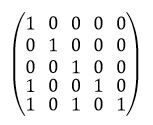
Здесь, например, R₄₁ = 1, так как четвертый элемент области задания (число 8) находится в отношении «делиться без остатка» со вторым элементом (числом 2).

Задание 4

Граф задан матрицей смежностей по вершинам или инцидентностей. Не рисуя граф, по заданной матрице определить основные сведения о нем: ориентированный или нет, количество вершин и ребер, наличие петель, кратных ребер. Построить для графа другое матричное задание: если задана матрица смежностей по вершинам, то построить матрицу инцидентностей; если задана матрица инцидентностей – построить матрицу смежностей по вершинам. В тех вариантах, где это возможно, задать граф также аналитически.

Матрица смежностей по вершинам:

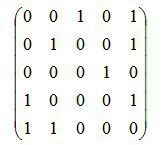
Решение:

Граф ориентированный. Следует из свойства матриц смежности: «Матрица смежности неориентированного графа является симметричной. Для ориентированного графа это, вообще говоря, неверно». В нашем случае матрица – несимметричная.

Граф имеет 5 вершин. Следует из определения: «Размерность матрицы mxm, где m – количество вершин графа». В нашем случае размерность матрицы – 5x5.

Аналитическое задание графа – это его представление в виде отношения. Область задания отношения (множество вершин) в данном случае следующая: X = {1,2,3,4,5}. Собственно отношение (т.е. множество пар смежных вершин) имеет следующий вид:

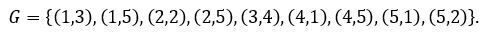
Граф имеет 9 ребер, 1 петлю. Кратных ребер нет. Следует из аналитического задания графа.

Матрица инцидентностей – матрица размерностью m×n, где m – количество вершин, n – количество ребер графа. Значения элементов матрицы определяются следующим образом:

- S_ij = -1, если -е ребро заходит в -ю вершину;

- S_ij = 1, если -е ребро выходит из -ой вершины;

- S_ij = 0, если -я вершина и  -е ребро не инцидентны.

Если -е ребро – петля при -ой вершине, то указывается S_ij = 1.

Построим матрицу инцидентностей.

Ее размерность – 5 × 9, так как у графа пять вершин и девять ребер. Матрица имеет следующий вид: