Лабораторна робота №7, Аналіз часових рядів із застосуванням системи EViews, Побудова ARIMA – моделі

« Назад

Мета: вивчення порядку і засобів побудови ARIMA - моделі для аналізу часових рядів з використанням системи Econometrics Views.

Хід роботи

Виконати наведені у методичних рекомендаціях приклади, відповідні вікна з результатами зберегти у файлі zvit_7_Прізвище.doc.

Методичні рекомендації щодо побудови ARIMA – моделі

Побудова адекватної ARIMA – моделі можлива при правильній специфікації її параметрів. Як правило, така процедура основана на аналізі корелограми часового ряду. За її допомогою дослідники визначають можливі величини параметрів моделі. Припустимо, що необхідно оцінити модель ARIMA (2, 2, 1) відносно змінної gdp. В такому випадку в якості залежної змінної регресії вказують функцію d, яка знаходить прирости відповідного порядку заданої змінної. Запис d(gdp) означає, що залежною змінною буде величина Δgdp_t = gdp_t – gdp_t-1. Якщо операцію взяття різниці слід використати декілька разів, то у функції вказується другий параметр. Вираз d(gdp, 2) знаходить величину Δ²gdp_t = Δ(gdp_t – gdp_t-1) = gdp_t – 2gdp_t-1 + gdp_t-2.

Для побудови регресії з AR чи MA компонентами використовуються функції ar та ma. Параметри цих визначають номер відповідного лога, який слід включити до моделі. Для кінцевого запису моделі ARIMA (2, 2, 1) слід записати: d(gdp, 2) с ar(1) ar(2) ma(1).

Програма видає результат оцінки моделі (рис. 1). Крім стандартного регресійного виводу видається інформація про корені рівнянь, за допомогою яких можна визначити стаціонарність процесу та його перетворювальність. В нашому випадку абсолютне значення коренів близьке до 1, що вимагає проведення додаткових тестувань та наявність одиничного кореня.

При потребі до ARIMA – моделі можна додати сезонний компонент. Наприклад, для квартальних даних варто додати сезонність з кроком 4, що перетворює модель ARIMA (2, 2, 1)

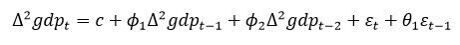
на модель

 

Для оцінки моделі необхідно записати: d(gdp, 2) с ar(1) ar(2) sar(4) ma(1).

Результати оцінки представлені на рис. 2. Для включення сезонних доданків для шоків слід застосовувати функцію sma з вказуванням необхідного номеру лагу.

Рис. 1 - Оцінка моделі ARIMA(2, 1, 1)

Рис. 2 - Оцінка моделі ARIMA(2, 1, 1) з сезонними доданками

Корелограма залишків останньої побудованої моделі (рис. 3) свідчить, що для всіх значень лагів від 1 до 16 приймається гіпотеза про відповідність залишків процесу білого шуму (всі значення Prob>0,05).

Побудуємо прогнози за отриманою моделлю на наступні 5 кварталів. Для цього змінимо діапазон даних на «1998:1-2006:4», та використаємо у вікні оціненої моделі кнопку Forecast (рис. 4). У вікні обирається змінна, яку слід прогнозувати, в нашому випадку gdp. Також вказується новий ряд, що міститиме прогнозні величини (gdpf), період прогнозування (з четвертого кварталу 2005 року до 4 кварталу 2006 року), вибирається динамічний метод прогнозування.

Рис. 3 - Корелограма залишків оціненої моделі ARIMA(2, 1, 1) з сезонними доданками

Завдання 1. Виділити з часового ряду тренд за допомогою методу Ходріка-Прескотта. Провести нормування залишків за правилом:

Перевірити новий ряд на відповідність процесу «білого шуму».

Завдання 2. Для отриманого у завд. 1 ряду за допомогою аналізу корелограми та графіку часткової кореляційної функції визначити параметри ARMA–моделі. Оцінити модель.

Завдання 3. Побудувати та оцінити найкращу ARIMA модель для кожного часового ряду бази даних. Для визначення порядку інтегрованості процесу застосувати тестування на наявність одиничного кореня.

Завдання 4. Для обчислених моделей (завд.1 – 3) побудувати прогнози, обчислити похибки прогнозування.

Завдання 5. Порівняти отримані моделі (завд. 1–3) на основі

• числових критеріїв;

• точності прогнозів;

• стабільності моделей. 

Завдання 6. Знайти параметри моделі AR(2), якщо:

Завдання 7. Знайти параметри моделі ARMA(1, 1), якщо

Методичні рекомендації щодо виконання завдання 1

Фільтр Ходріка-Прескотта. Цей метод використовується для виділення трендового компонента у довгостроковому періоді. Для застосування методу слід вибрати змінну та виконати команду Procs→Hodric-Prescott Filter…. У вікні (рис. 4) слід вказати назву нового ряду, що міститиме оцінку трендового компонента, і параметр згладжування.

Рис. 4 - Побудова методу Ходріка-Прескотта

В результаті виконання команди EViews створює нову змінну hp_gdp та виводить графік, на якому розташовані вихідний та обчислений ряди (рис. 5).

Рис. 5 - Виділення тренду за допомогою фільтру Ходріка-Прескотта