Лекция №5, Принятие решений в условиях неопределенности и риска

« Назад

 

1. Имитационное моделирование

Особым видом моделей являются имитационные модели. Имитационное моделирование производится в тех случаях, когда исследователь имеет дело с такими математическими моделями, которые не позволяют заранее вычислить или предсказать результат. В этом случае для предсказания поведения реальной сложной системы необходим эксперимент, имитация на модели при заданных исходных параметрах. Имитация представляет собой численный метод проведения на ЭВМ экспериментов с математическими моделями, описывающими поведение сложной системы в течение заданного или формируемого периода времени. При построении имитационной модели интересна возможность вычисления некоторого функционала, заданного на множестве реализаций процесса функционирования изучаемой системы.

Вероятностный характер процессов, происходящих в сложных системах, приводит к невозможности аппроксимации явлений функциональными зависимостями, здесь используют алгоритмическое описание. В моделях задают некоторые средние характеристики и при данных значениях проводят расчеты.

Технология имитационного моделирования появилась в 60-х г. XX в., и на протяжении многих лет она не только остается одной из основных в исследовании операций, но и бурно развивается в области реинжиниринга бизнес-процессов и новых направлений искусственного интеллекта.

Основу этой технологии составляет компьютерный имитационный эксперимент, связанный с воспроизведением динамических процессов функционирования исследуемой системы.

В процессе такого воспроизведения осуществляется наблюдение за функционированием модели и выявление «узких мест» в организации деятельности.

При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы во времени. При этом имитируются элементарные явления, составляющие процесс с сохранением их логической структуры и последовательности протекания во времени. В результате по исходным данным получают сведения о состоянии процесса в определенные моменты времени, дающие возможность оценить характеристики системы.

Основными достоинствами этого метода являются:

- возможность воспроизведения реальной системы с практически любым видом детальности;

- повторяемость эксперимента;

- возможность произвольной фрагментации и структуризации системы.

2. Модели систем массового обслуживания

С использованием имитационного моделирования.

Модели теории очередей, или модели оптимального обслуживания (массового обслуживания) используются для определения оптимального числа каналов обслуживания по отношению к потребности в них. Применяется в различных ситуациях, где есть клиенты и пункты их обслуживания (резервирование билетов по телефону, обслуживание клиентов в банке, количество разгрузочных площадок на складах и т.д.).

Используются для уравновешивания расходов на дополнительные каналы обслуживания и потерь от обслуживания на уровне ниже оптимального. Например, если клиент в банке слишком долго ждет своей очереди на обслуживание, у него может возникнуть желание поменять банк. Следовательно, необходимо увеличить численность персонала, обслуживающего клиентов. На сколько человек необходимо увеличить численность поможет модель теории очередей.

Модели теории массового обслуживания находят применение при решении задач системного анализа в случае, когда исследуемые величины имеют случайный характер. К числу таких задач относятся задачи управления запасами при случайном спросе, задачи организации работы предприятий торговли, связи, бытового и медицинского обслуживания, технического обслуживания предприятий, автомобилей и др.

Всякая система массового обслуживания (СМО) предназначена для обслуживания определенного потока заявок, поступающих в случайные моменты времени. Обслуживание заявок продолжается какое-то, в общем случае случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени на входе в СМО может образоваться очередь, в другие периоды времени каналы могут работать с недогрузкой или вообще простаивать.

Процессы работы СМО представляют собой случайный процесс с дискретным состоянием и непрерывным временем. Состояния системы меняются скачком в моменты реализации событий (поступление новой заявки или окончание обслуживания заявки или когда заявка, которой надоело ждать, покидает очередь).

Задача теории массового обслуживания состоит в построении моделей, связывающих заданные условия работы СМО с интересующими показателями эффективности системы, описывающими ее способность справляться с потоком заявок (требований).

Для всякой СМО характерна структура, которая определяется составом элементов и связями между ними. Основными элементами являются:

- входящий поток заявок;

- каналы обслуживания;

- очередь заявок;

- выходящий поток заявок.

Схематично изображение СМО показано на рис. 1.

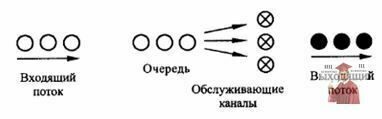
Рис. 1 - Схема многоканальной СМО с ожиданием

Для описания входящего потока требуется определить количество заявок в начальный момент времени, при этом следующая заявка поступает через случайное время, которое имеет определенный закон распределения.

Очередь определяет принцип, в соответствии с которым поступающие на вход обслуживающей системы заявки подключаются из очереди к процедуре обслуживания. Различают системы с неограниченным временем ожидания (при любой очереди дожидается обслуживания), системы с отказами (когда все каналы обслуживания заняты, заявка покидает систему) и системы смешанного типа (ожидает обслуживания, но некоторое ограниченное время). Также важны дисциплины обслуживания (FIFO, по приоритетам, случайный выбор, LIFO – редко).

Механизм обслуживания определяется характеристиками процедуры обслуживания. К характеристикам относят продолжительность обслуживания (может быть различна в разных каналах), является величиной случайной.

В качестве основных критериев эффективности функционирования систем массового обслуживания, в зависимости от характера решаемой задачи могут выступать:

- вероятность немедленного обслуживания поступившей заявки;

- вероятность отказа в обслуживании поступившей заявки;

- относительная и абсолютная пропускная способность системы;

- средний процент заявок, получивших отказ в обслуживании;

- среднее время ожидания в очереди;

- средняя длина очереди;

- средний доход от функционирования системы в единицу времени и т.п.

Наименьшей единицей работы является активность. Активность является объектом, потребляющим время. Логически связанный набор активностей образует процесс. Активности инициируются в результате совершения событий. Событие представляет собой мгновенное изменение состояния некоторого объекта системы, который может быть, как пассивным, так и активным.

Построение модели состоит из решения двух основных задач: описания правил, задающих различные виды процессов и указания значений атрибутов процессов или правил генерации этих значений.

Способ моделирования процесса – это задание его длительности либо дискретной величиной, либо с помощью случайных величин с заданием закона распределения: нормального, экспоненциального, гамма-распределения и др. Эмпирические ряды распределения, получаемые при обработке статистических данных, оформляются в таблицах или изображаются графически посредством геометрических образов. Построение эмпирических графиков и диаграмм позволяет установить на первом этапе исследования, к какому типу теоретических распределений ближе всего полученное эмпирическое распределение, что облегчает выбор конкретных технических приемов обработки исходных данных.

В реальной системе совместно выполняются несколько активностей, принадлежащих как связанным, так и не связанным между собой процессам. Поведение системы во времени отображается порядком следования событий, установленным на уровне глобальных переменных. Наиболее важную роль в моделировании играют моменты, когда заканчиваются активности, все события в системе происходят именно в эти моменты времени.

Для реализации имитационного моделирования необходимо выбрать состав контролируемых характеристик системы. Далее необходимо перейти к математической постановке задачи и собственно к построению модели.

Технология имитационного моделирования на основе использования системы MicroSaint является одной из наиболее простых и адекватных программ исследования систем операционного и производственного менеджмента. Система не русифицирована.

3. Система «Micro Saint»

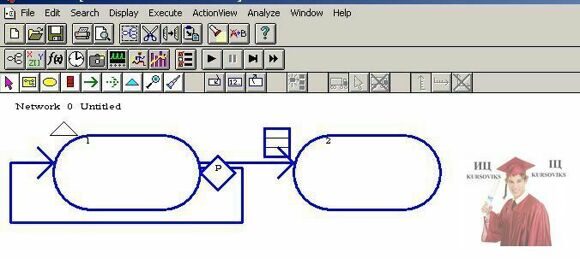
Модель исследуемой системы должна быть представлена в виде сетевой структуры (рис. 2).

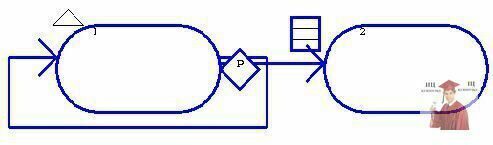
Рис. 2 - Сетевая структура модели

Условные графические изображения на сетевой структуре:

- овалы - блоки действий (задачи);

- стрелки - пути перемещения динамических объектов (тэгов);

- ромбы - разветвления путей перемещения тэгов;

- таблички - очереди тэгов;

- маленький треугольник - точка ввода тэгов в модель.

Конструирование структуры осуществляется использованием «подсвеченных» кнопок нижней панели инструментов окна системы (рис. 3)

Рис. 3 - Окно для конструирования модели

Для описания характеристик системы используются переменные, которым присваиваются значения с помощью оператора присваивания «:=».

Например, переменной Status присвоить значение 1: Status:=1;

Переменные характеризуются типом, определяющим ее возможные значения.

В системе возможны четыре типа переменных: Integer (целочисленная переменная), Real (действительное число), Аrray of Integers(массив из целых чисел), Array of Real(массив из действительных чисел). Все переменные модели должны быть внесены в список переменных, который открывается кнопкой 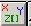 (средний ряд панелей инструментов, вторая кнопка слева).

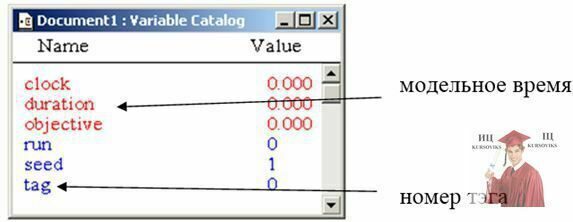
Рис. 4 - Окно списка переменных (все перечисленные переменные на рисунке являются системными, т.е. такими, которые используются в любой модели)

Ввести переменную в список можно нажатием кнопки Accept  (нижний ряд панели инструментов).

Ввод переменных происходит в окне описания переменной (рис. 5), где задается:

- имя переменной (Name);

– тип переменной (Type);

- исходное начальное значение переменной, которое определяет первоначальное состояние системы (Initial Value).

Purpose – цель, результат.

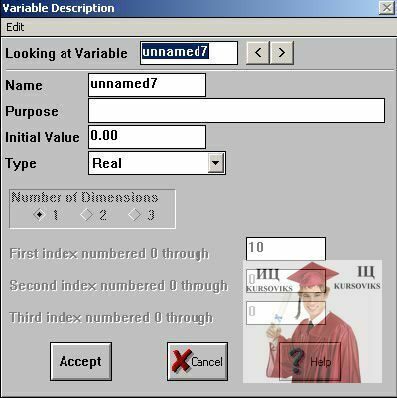
Рис. 5 - Окно описания переменных

Для запуска имитации деятельности предприятия необходимо описать задачу, регистратор очереди и разветвитель, из которых конструируется модель. Описание осуществляется в окнах описания, которые вызываются «двойным кликом» на соответствующем элементе сетевой структуры.

3.1. Описание задачи

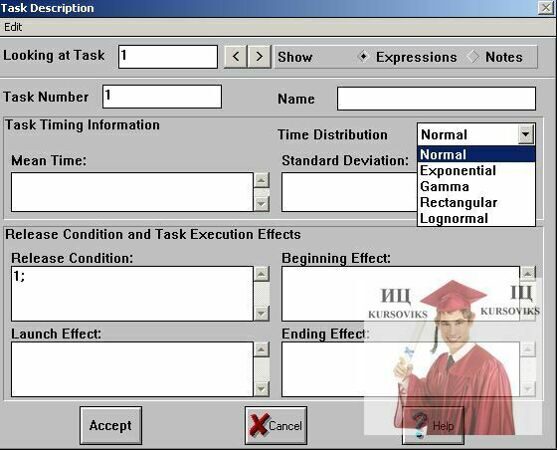
Рис. 6 - Описание задачи

LookingatTask– просмотр задач из списка;

Task Number – номер задачи;

Name – имя задачи;

Time Distribution – поле для определения закона распределения вероятностей,

Mean Time – среднее значение времени распределения;

Standard Deviation – стандартное отклонение;

ReleaseCondition – условие возможного входа тэга в соответствующий блок;

BeginningEffect – описание действия, которое необходимо выполнить при входе тэга в блок;

LaunchEffect – описание действия при прерывании обслуживания тэга;

EndingEffect– описание действия при выходе тэга из блока.

3.2. Описание регистратора очереди

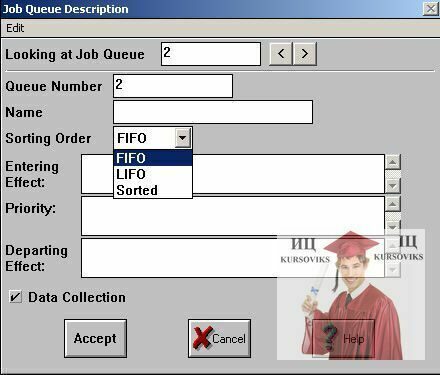
Рис. 7 - Описание регистратора очереди

LookingatJobQueue – просмотр очередей из списка;

Queue Number – номер очереди;

Name – имя элемента в очереди;

SortingOrder – поле для определения порядка выхода из очереди;

EnteringEffect – описание действия, которое необходимо выполнить при входе тэга в блок;

Priority –выражение, которое позволяет покинуть очередь тот тэг, для которого значение выражения становится максимальным;

DepartingEffect– описание действия при выходе тэга из очереди.

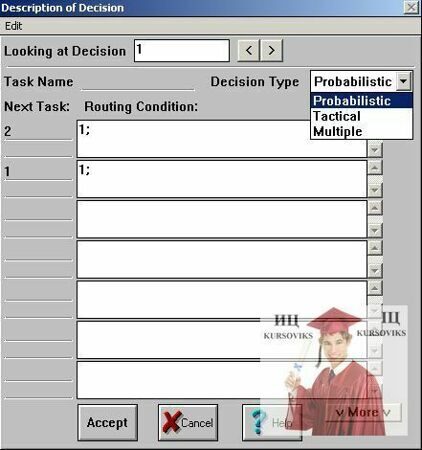
3.3. Описание разветвителя

Рис. 8 - Описание разветвителя

LookingatDecision – просмотр разветвлений из списка;

TaskName – имя задачи;

DecisionType - тип разветвления;

Multiple-создает множество копий тэга, вошедшего в разветвитель, и отправляет на все выходы разветвителя. Моделирует параллельные (одновременно протекающие процессы) в исследуемой системе;

Probabilistic- определяет стохастический (случайный) механизм выбора тэгом направления дальнейшего движения;

Tactical- использует поляRoutingCondition для записи выражений, которые определяют направление дальнейшего движения.

3.4. Этап проведения компьютерного эксперимента с моделью

После составления описаний всех элементов модели она может быть запущена для выполнения задач. Для запуска и управления процессом выполнения модели используется правая часть средней панели инструментов.

Рис. 9 - Правая часть средней панели инструментов

Кроме кнопок этой панели можно также обратиться к разделу Execute главного меню системы.

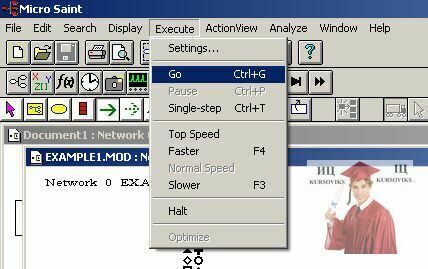
Рис. 10 - Раздел Execute

3.5. Остановка модели

Существует два способа остановки модели: «вручную» (меню Execute, оператор Halt) и по определенному условию (достижения в модели определенного состояния).

Второй способ связан с размещением оператора останова halt() в определенных местах описания модели. Например, размещение оператора halt() в поле очереди Entering Effect приведет к тому, что когда первый тэг войдет в очередь и произойдет вычисление этого эффекта, модель будет остановлена.

3.6. Сбор результатов компьютерного эксперимента

Целью любого компьютерного эксперимента - сбор информации о значениях переменных модели, наблюдаемых в процессе проведения эксперимента, и состояниях очередей, возникающих в процессе моделирования. Переменные, которые могут наблюдаться в эксперименте, составляют коллекцию переменных. Для одной и той же модели могут быть определены несколько разных коллекций, отличающихся друг от друга составом переменных и условиями, при которых осуществляется регистрация их значений.

Список коллекций открывается нажатием кнопки с портфелем . Если для разработанной модели не определено ни одной коллекции, этот список пуст.

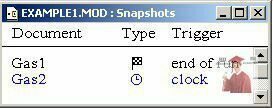
Рис. 11 - Список коллекций

Для определения коллекции следует нажать кнопку  при открытом списке коллекций. При этом открывается окно описания коллекции.

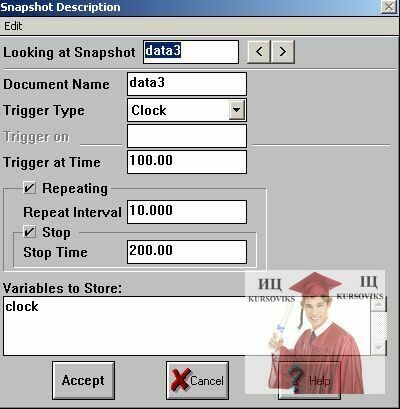
Рис. 12 - Определения коллекции

DocumentName - имя коллекции.

VariablestoStore — список имен переменных, которые включаются в коллекцию.

В этом же окне указываются условия, при которых будут регистрироваться значения переменных коллекции:

TriggerType– список условий сбора значений переменных в эксперименте;

TriggeratTime – время начала регистрации данных;

Repeat Interval – величина интервала модельного времени, через который необходимо регистрировать данные;

StopTime – время остановки модели.

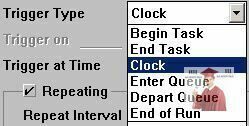
Рис. 13 - Clock - сбор данных по таймеру

BeginTask – сбор данных осуществлять в момент входа тэга в блок задач (задача указывается в Triggeron)

EndTask - сбор данных осуществлять в момент выхода тэга из блока задач (задача указывается в Triggeron)

BeginQueue – сбор данных осуществлять в момент входа тэга в очередь (очередь указывается в Triggeron)

EndQueue - сбор данных осуществлять в момент выхода тэга из очереди (очередь указывается в Triggeron)

EndofRun – сбор данных осуществлять только в момент окончания прогона модели

Clock - сбор данных по таймеру с учетом заданной в Repeat Intervalвеличины.

Выбор одного из этих вариантов будет определять условия сбора значений всех переменных коллекции.

При необходимости внесения изменений в коллекцию (добавление или удаление переменных) можно открыть окно описания коллекции двойным кликом на строке коллекции в списке Snapshot.

3.7. Определение параметров прогона модели

Перед запуском модели необходимо определить, в каком режиме будет проходить моделирование (выполняться прогон модели). Для ввода такой информации следует нажать кнопку определения параметров прогона , при этом на экране монитора появляется окно для установки параметров прогона.

В этом окне отмечаются функции, которые будут реализованы в процессе прогона модели.

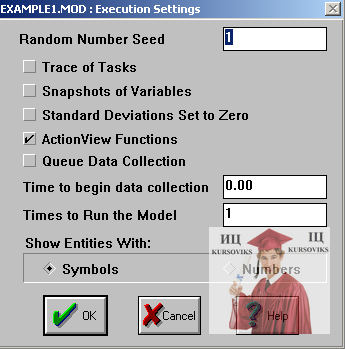
Рис. 14 - Определения параметров прогона

1. TraceofTasks (трассировка задач).

2.SnapshotsofVariables (сбор значений переменных).

3.StandartDeviationsSetbyZero (не используется для простых задач).

4. ActionViewFunctions (анимация).

5.QueueDataCollection (сбор данных о состояниях очередей).

6.TimetobeginDataCollection(модельное время начала сбора данных).

7. TimestoRuntheModel(номер прогона модели).

8. ShowEntitiesWith(форма показа динамических объектов — тэгов, символами или их количеством, обычно символами).

Второй и пятый из этих пунктов необходимы для сбора результатов, остальные реализуют вспомогательные функции.

После установки параметров прогона при запуске модели система автоматически запрашивает информацию об именах файлов, в которых необходимо собирать информацию. Обычно имена таких файлов совпадают либо с именем модели, либо с именем коллекции переменных.

3.8. Структуры файлов результатов

На рис. 5 проведена структура файла с данными о состояниях очередей (тип файла *.que), который формируется при отмеченном флажке Queue Data Collection.

Рис. 15 - Фрагмент файла результатов прохождения тэгов через очередь (файл типа *.que)

Описание столбцов таблицы (рис. 15):

1) clock - - момент времени, в который изменилось состояние очереди;

2) tag - номер объекта-тэга, который был активен в заданный момент времени;

3) run - номер прогона программы модели (не информативен);

4) length -длина очереди тэгов в указанный момент времени;

5) wait - время ожидания в очереди активного тэга;

6) Trigger - характер изменения состояния очереди.

В поле Trigger встречаются значения четырех видов:

- Start - старт для работы с очередью;

- Enter - вход тэга в очередь;

- Depart - выход тэга из очереди;

- Bypass - проход тэга через очередь без задержки, т. е. через пустую очередь.

При отмеченном флажкеSnapshots of Variables осуществляется сбор значений переменных, которые указаны в элементе Variables to Store окна описания коллекции. Собранная информация сохраняется в файле с расширением *.res. Данные в файле представлены в виде таблицы, структура которой похожа на приведенную на рис. 5. Однако, в ней содержатся столбцы со значениями только указанных в коллекции переменных.

4. Анализ результатов эксперимента

Результаты эксперимента могут быть проанализированы с использованием методов, инкапсулированных в меню Анализ (Analyze). Эти методы позволяют представить результаты прогона модели в наглядной, лаконичной форме графика или таблицы. Использование методов анализа призвано способствовать выявлению «узких мест» в организации исследуемой системы и принятию управленческих решений по реорганизации бизнес-процессов.

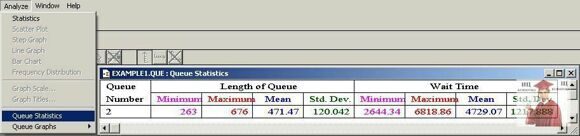
4.1. Статистика очереди

Файлы результатов с расширением *.que анализируются методами «Статистика очереди» (QueueStatistics) и «Графы очереди» (QueueGraphs). Для вызова этих методов необходимо открыть соответствующий файл (сделать окно с файлом активным) и выбрать в меню нужный метод.

Рис. 16 - Статистика очереди

В таблице на рис. 16 (пункт меню Queue Statistics) представлены характеристики длины очереди (Length of Queue) и времени пребывания тэга в очереди (Wait Time) (Меаn — среднее значение, Std.Def. — Standart Deviation — среднеквадратичное отклонение для каждой из характеристик).

На рис. 17 (пункт меню Queue Graphs) представлены графики характеристик очереди.

Рис. 17 - Графики характеристик очереди

4.2. Зависимости

Методы анализа файла с расширением *.res можно разделить на две группы: построение зависимостей и построение гистограмм. Построение зависимостей выполняется в три этапа:

- разметка координатных осей будущего графика зависимости;

- оформление графика (название зависимости, названия осей, диапазоны и т. п.);

- выбор формы представления графика зависимости.

Разметка координатных осей графика связана с использованием правой части нижнего ряда панели инструментов (рис. 18). Для разметки необходимо «перетащить» кнопку горизонтальной оси с панели инструментов в тот столбец таблицы файла, который будет определять значения горизонтальной оси.

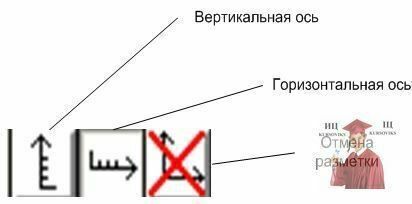
Рис. 18 - Инструменты разметки

Аналогично перетаскивается кнопка вертикальной оси (оси ординат). Однако, в отличие от горизонтальной оси, она может быть перетащена на нескольких столбцов таблицы файла. В этом случае в рамках одного графика будет построено несколько зависимостей. Кнопка удаления разметки «стирает» (отменяет) ранее помеченные элементы путем ее «перетаскивания» в соответствующие столбцы файла.

Оформление графика реализуется методами «Шкала графика» и «Заголовки графика» (GraphScale, GraphTitles) меню Анализ.

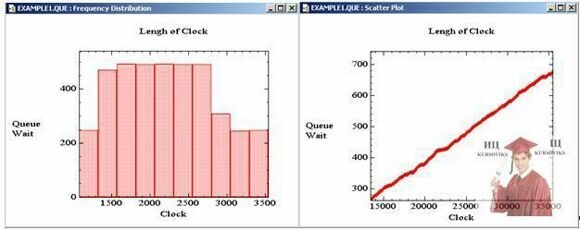
4.3. Гистограммы

Гистограмма (FrequencyDistribution) — это особый вид графика, для разметки которого указывается только одна горизонтальная ось (ось абсцисс). Столбец файла, используемый для определения такой оси, сортируется:

- определяется максимальное значение, содержащееся в этом столбце (Мах);

- определяется минимальное значение, содержащееся в этом столбце (Мin);

- диапазон (Мах—Мin) делится на заданное число интервалов (Int) одинаковой ширины: w=(Мах – Мin)/Int.

После этого в процессе сортировки подсчитывается количество значений Li, i = 1 ¸ Int, попадающих в каждый из таких интервалов. Подсчитанные таким образом величины Li выводятся на вертикальную ось графика гистограммы. Гистограмма интерпретируется обычно как показатель эффективности использования того или иного оборудования в течение определенного интервала времени.

Оформление графика гистограммы выполняется теми же методами, что и для обычных зависимостей.

5. Операции процедурного языка

Таблица

Основные операции языка

Приоритет	Знак операции	Типы операции
0	!	Операция логического отрицания «НЕ»
1	* / %	Умножение, деление, остаток от деления
2	+ -	Сложение, вычитание
3	< > <= >=	Отношение (меньше, больше и т.д.)
4	= = <>	Отношение (равно, не равно)
5	&	Логическое И
6	|	Логическое ИЛИ
7	:=	Присваивание

5.1. Основные операторы процедурного языка

Ifусловие then оператор1 else оператор2;

- условный оператор

If условие then оператор1, оператор2, оператор3; - условный оператор

while условие do оператор1;

- цикл

random(); - функция генерирует случайное число на отрезке [0;1]

b+=1; c-=1;

- добавляет, вычитает соответственно единицу из переменной.

6. Законы распределения

1. Нормальное распределение

Его плотность имеет вид:

,

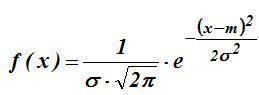где m – математическое ожидание, - с.к.о. Обычно рассматривается нормальное распределение с m=0 и 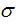=1, т.е. N(0,1).

2. Равномерное (прямоугольное) распределение

Его плотность:

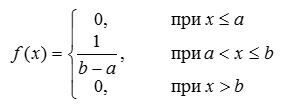
где a и b – границы интервала. Для данного закона .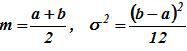

3. Показательное (экспоненциальное) распределение

Его плотность:

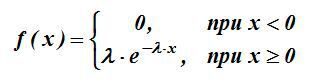
Для данного закона .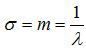

4. Логнормальное распределение

Его плотность:

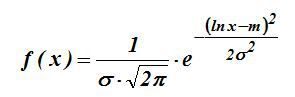
5.Гамма распределение

Его плотность имеет вид:

.

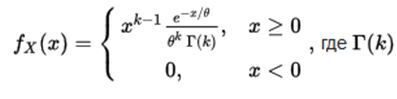7. Теория игр и принятие решений

При принятии управленческих решений о функционировании и развитии экономического объекта необходимо учитывать важную характеристику внешней среды – неопределенность. Под неопределенностью понимаю отсутствие, неполноту, недостаточность информации об объекте, процессе, явлении или неуверенность в достоверности информации. Неопределенность является характеристикой внешней среды (природы), которая может находиться в одном из множества возможных состояний. Неопределенность обусловливает появление ситуаций, не имеющих однозначного исхода (решения), особое место занимает ситуация риска.

Данные, необходимые для принятия решения в условиях неопределенности, обычно задают в форме матрицы, строки которой соответствуют возможным действиям (управленческим решениям), а столбцы – возможным состояниям природы. В ячейках матрицы находятся результаты (исходы) при выборе конкретного действия в конкретном состоянии. Мера несоответствия между разными возможными результатами принятия определенных стратегий, т.е. разность между результатом, который можно получить, если знать действительное состояние природы, и полученным результатом, называется риском.

Под ситуацией риска следует понимать сочетание, совокупность различных обстоятельств и условий, создающих обстановку того или иного вида деятельности с возможностью количественно и качественно определить степень вероятности того или иного варианта. Для того, чтобы снять ситуацию риска, ЛПР вынуждено принимать решения и стремиться реализовать их.

В условиях риска – когда, например, доход от реализации продукции описывается с помощью функции распределения, но не является фиксированной величиной.

В условиях неопределенности – функция распределения неизвестна, т.е. может принимать пять значений, но неизвестны вероятности этих значений.

С точки зрения полноты исходных данных определенность и неопределенность представляют два крайних случая, а риск определяет промежуточную ситуацию, в которой приходится принимать решение.

Выбор критерия принятия решения в условиях неопределенности является наиболее сложным и ответственным в исследовании операций.

Теория, в которой рассматриваются задачи принятия решений в условиях неопределенности двумя или более разумными противниками, каждый из которых стремится оптимизировать свои решения за счет других, известна как теория игр.

Игра – это совокупность правил, описывающих сущность конфликтной ситуации. Правила игры устанавливают: выбор образа действий игроков на каждом этапе игры; информацию, которой обладает каждый игрок на каждом шаге; плату для каждого игрока на каждом этапе.

8. Обсуждение

Методы проведения системных исследований		Задачи системного анализа
Имитационное моделирование		Системы массового обслуживания
Теория игр и принятия решений		Принятие решения в условиях неопределенности и риска
Линейное программирование	целочисленное	Принятие решения в условиях определенности
Линейное программирование	целочисленное	Транспортные задачи
Сетевое планирование (теория графов)		Управление проектами