Семінар Методика проведення досліджень за вибіркою
Код роботи: 824
Вид роботи: Семінар
Предмет: Соціологія
Тема: Особливості проведення розслідувань та публікація їхніх результатів
Кількість сторінок: 15
Дата виконання: 2016
Мова написання: українська
Ціна: безкоштовно
1. Причини і умови застосування вибіркового спостереження, його завдання, основні поняття
2. Формування вибіркової сукупності. Види та схеми відбору. Мала вибірка
3. Похибки вибірки. Визначення обсягу вибірки. Оцінка істотності вибіркових характеристик та способи поширення вибіркових даних
1. Причини і умови застосування вибіркового спостереження, його завдання, основні поняття
Вибіркове спостереження є найпоширенішим з усіх видів несуцільногоспостереження. Під час проведення вибіркового спостереження вивчаються не всі одиниці досліджуваного об’єкта, а лише деяка відібрана частина цих одиниць. Однак спостереження організоване таким чином, що ця частина відібраних одиниць відображає всю сукупність наче у зменшеному масштабі.
Загальну сукупність однорідних об’єктів (одиниць) з якої здійснюється відбір для дослідження у статистиці називають генеральною сукупністю.
Відібрана для обстеження частина генеральної сукупності має назву вибірки або вибіркової сукупності. На підставі результатів дослідження вибіркової сукупності можназробити висновки про властивості генеральної сукупності, тобто теоретичні характеристики замінити статистичними.
До теоретичних (шуканих) характеристик належать узагальнювальні показники генеральної сукупності – середній розмір ознаки (Хсер.), частка (Р), генеральна дисперсія (σ2), які називають параметрами.
Статистичними характеристиками (оцінками) є характеристики вибіркової сукупності – середня вибіркова (Хсер.в.), вибіркова частка (W), вибіркова дисперсія (σ2 в.), які називають статистиками.
Отже завдання вибіркового спостереження – за результатами обстеженої частини надати характеристику усій сукупності в цілому.
Переваги вибіркового спостереження перед суцільним:
- практичність (іноді немає можливості чи недоцільно здійснювати суцільне спостереження, наприклад, контроль якості книжкової продукції – підручників, дитячої книги тощо);
- висока точність результатів за рахунок зниження помилок реєстрації (наприклад, соціологічні чи інші наукові дослідження, що вимагають професійних знань суті явища);
- проведення статистичних досліджень, пов’язаних із знищенням зразків (перевірка якості харчової продукції, екологічного стану та інше);
- мінімальні затрати, швидкість дослідження, детальніше вивчення кожної одиниці спостереження.
Зверніть увагу! Ці переваги вибіркового спостереження мають місце лише за умов дотримання наукових принципів його проведення, що надає можливість отримати репрезентативну вибірку, яка відтворює характеристики генеральної сукупності. Порушення цих принципів, коли спостереженню підлягають одиниці, відібрані на основі суб’єктивного погляду дослідника, призводять до того, що результати такого спостереження мають відношення не до усієї генеральної сукупності, а тільки до тієї її частини, яка була піддана спостереженню.
Вибірка вважається репрезентативною, якщо кожен елемент генеральної сукупності має однакову ймовірність (рівну можливість) потрапити у вибірку і відбір здійснюється строго випадковим чином за схемами, розробленими математичною статистикою. А також, коли обсяг вибіркової сукупності є достатнім.
Вибіркове спостереження здійснюється у такій послідовності:
- обґрунтування мети, складання програми;
- визначення необхідної частки (5%, 25%, 50% чи ін.) одиниць для обстеження та способу їх відбору до вибіркової сукупності;
- формування вибірки;
- узагальнення даних спостереження і визначення їхніх вибіркових характеристик (оцінок відповідних характеристик генеральної сукупності);
- обчислення похибок вибірки, перевірка надійності результатів;
- поширення вибіркових даних на всю досліджувану сукупність (висновки про параметри генеральної сукупності).
Точність результатів вибіркового спостереження залежить від способу відбору одиниць, варіації ознаки в сукупності і від кількості відібраних одиниць.
2. Формування вибіркової сукупності. Види та схеми відбору. Мала вибірка
Система правил відбору одиниць і способів характеристики досліджуваної сукупності складає зміст вибіркового методу.
Розрізняють такі способи формування вибіркових сукупностей:
- власне випадковий (простий випадковий) відбір;
- механічний (систематичний);
- типовий (районований);
- серійний (гніздовий);
- комбінований;
- багатоступінчастий та багатофазний.
Усі види відбору (крім механічного) можуть бути проведені повторним чи безповторним методом, який визначає можливість для відібраної одиниці продовжувати участь в процедурі відбору. Механічний добір завжди є безповторним.
Повторним називають відбір, при якому відібрана одиниця повертається назад угенеральну сукупність і може повторно брати участь у вибірці. При такому доборі шанси (ймовірність) кожної окремої одиниці потрапити у вибірку залишаються постійними.
Безповторним є відбір, у якому відібрана одиниця не повертається до генеральноїсукупності і в подальшій вибірці участі не бере. В цьому випадку ймовірність одиниці потрапити до вибірки постійно змінюється – для залишившихся одиниць вона зростає.
При достатньо великому обсязі генеральної сукупності, оцінки її характеристик, отримані на основі безповторної вибірки, істотно не відрізняються від оцінок, отриманих на основі повторної вибірки.
Випадкова вибірка – це класичний спосіб формування вибіркової сукупності,який передбачає попередню досить складну підготовку до формування вибірки. Дає добрі результати за умов однорідності сукупності.
Простий випадковий добір проводиться жеребкуванням або за допомогою таблиць випадкових чисел без будь-яких елементів системності (без попереднього розчленування генеральної сукупності на окремі групи). Для жеребкування на кожну одиницю генеральної сукупності необхідно заготувати відповідну фішку, шар або картку з інформацією щодо окремої одиниці сукупності. При використанні таблиць випадкових чисел усі елементи сукупності мають бути пронумеровані. Необхідно також встановити чіткі межі генеральної сукупності таким чином, щоб присутність чи відсутність у ній окремих одиниць не викликала сумніву. Так, наприклад, при обстеженні студентів необхідно вказати, чи будуть прийматися до уваги особи, що перебувають в академічній відпустці. У великих за обсягом сукупностях така робота здебільшого недоцільна, а часом і неможлива, тому, незважаючи на простоту власно випадкового відбору, на практиці застосовуються інші різновиди випадкових вибірок, які представляють собою видозмінення простої випадкової вибірки.
Однією з найпоширеніших форм в практиці вибіркового спостереження є механічний відбір. Це послідовний вибір одиниць, який здійснюється за списками чибезпосередньо на місці дослідження через рівні проміжки в розташуванні цих одиниць у генеральній сукупності. Розташування одиниць сукупності буває впорядкованим (ранжированим) або невпорядкованим (випадковим) відносно досліджуваної ознаки. Наприклад, список співробітників Інституту в порядку зменшення заробітної плати або список студентів за алфавітом. Генеральна сукупність розбивається на рівні за чисельністю одиниць групи (інтервали) і з кожної групи для обстеження вибирається одна одиниця. При цьому задається початок, крок відліку і обсяг вибірки.
Початок відліку залежить від способу розташування одиниць в генеральній сукупності. У випадку їх невпорядкованого розташування він може бути встановлений довільно або жеребкуванням з сукупності одиниць першого інтервалу. При впорядкованому розташуванні за початок відліку приймають одиницю, яка розташована всередині першого інтервалу, щоб уникнути систематичної помилки вибірки.
Крок відліку визначається співвідношенням обсягів генеральної та вибіркової сукупностей h = N/n, наприклад, з генеральної сукупності обсягом 1000 од. обстеженню підлягає 100 од. (1000 / 100 = 10), це означає, що з кожних 10 од. буде обрано для обстеження 1 од. (кожну 10-ту), крок відліку дорівнює 10.
Механічний відбір дуже зручно застосовувати у випадках, коли не можна заздалегідь скласти список одиниць генеральної сукупності, наприклад, у маркетингових дослідженнях можна спостерігати кожного 10-го покупця, що увійшов до магазину, при дослідженні самостійної роботи студентів кожного 5-го відвідувача читального залу бібліотеки та комп’ютерного класу. В такому разі вибірка береться з сукупності, яка формується поступово чи з практично нескінченної сукупності.
Типовий (розшарований, районований) добір орієнтований на забезпеченняпредставництва у вибірці відповідних типових груп генеральної сукупності. Формування вибірки іде з урахуванням структури генеральної сукупності. На відміну від простого випадкового та механічного добору, які проводяться в цілому по генеральній сукупності, типовий передбачає розділення (розшарування) її на якісно однорідні групи за якоюсь важливою типовою ознакою. Наприклад, при обстеженнях населення такими групами можуть бути, райони, соціальні, вікові чи освітні групи. Потім з кожної групи проводять незалежний відбір елементів простим випадковим чи механічним способом пропорційно питомій вазі (обсягу) групи у загальній сукупності.
Перевагою типового відбору є отримання більш достовірних результатів порівняно з попередніми відборами. Оскільки до вибірки потрапляють представники усіх типових груп ймовірність отримати більшу точність вибіркових даних тут вища.
Застосовувати цей метод відбору краще у разі неоднорідності одиниць досліджуваної сукупності.
Серійний добір зручно використовувати у тих випадках, коли одиниці сукупностіоб′єднані у невеликі групи чи серії, які розглядають як одне ціле.
Серії складаються з одиниць, які пов′язані або територіально (райони, селища), або організаційно (фірми, акціонерні товариства тощо). В якості серій можуть розглядатися упаковки з визначеною кількістю готової продукції, партії товару, студентські групи, творчі колективи та інше.
Вибіркова сукупність серій формується за схемами механічної або простої випадкової безповторної вибірки. Якщо серія потрапила до вибірки, то обстежують усі без винятку елементи серії, тобто проводять суцільне їх обстеження, а результати розповсюджують на всю сукупність. Цей спосіб відбору застосовують при перевірці якості продукції того чи іншого підприємства, роботи відділу, при атестації ВУЗу (у відібраних групах студентів роблять суцільне вимірювання залишкових знань) тощо.
Застосовуючи серійну вибірку, слід звернути увагу на те, що випадкова похибка цієї вибірки виходить дещо більшою, ніж при інших способах відбору. Щоб цьому запобігти необхідно збільшити обсяг вибірки.
У комбінованих вибірках, які є найбільш поширеними, поєднуються різні способи добору. На практиці можна комбінувати типову і серійну вибірки, коли серії відбирають у встановленому порядку з декількох типових груп. Можлива також комбінація серійного і простого випадкового доборів, при якій окремі одиниці відбирають всередині серії у випадковому порядку. Комбінують також суцільне і вибіркове спостереження, де вибіркове уточнює, підтверджує результати суцільного чи є його пробним варіантом.
Багатоступінчастий відбір характеризується тим, що на усіх ступенях, крімостаннього, проводиться лише відбір, а спостереження досліджуваних одиниць відбувається тільки на останньому ступені. Одиниці відбору на попередніх ступенях – це зазвичай організаційні об’єднання одиниць спостереження, їх певні групи.
Отже спочатку відбувається поступовий вибір з генеральної сукупності великих груп одиниць, потім груп, менших за обсягом і так доти, поки не оберуть ті одиниці, які підлягатимуть обстеженню. Ступенів може бути два, три і більше. На різних ступенях вибірки використовують різні одиниці і різні способи відбору. Наприклад, під час обстежень рівня знань студентів ВУЗів відбір населених пунктів, у яких є вищі навчальні заклади можна здійснювати типовим способом, ВУЗів – теж типовим чи випадковим, курсів, груп – серійним чи механічним, студентів – механічним чи випадковим.
При багатофазній вибірці на усіх фазах зберігається одна й та сама одиниця відбору, а кожна фаза відрізняється від попередньої обсягом вибірки та програмою обстеження. З генеральної сукупності формується первинна вибірка, а з первинної – підвибірка і т. д. На кожній наступній фазі обсяг підвибірки зменшується, а програма обстеження розширюється. Наприклад, під час дослідження ставлення студентів до організації навчального процесу в Інституті на 1-й фазі досліджують 25% від загальної чисельності студентів за короткою програмою (три запитання), на 2-й фазі – 15% за ширшою програмою, яка містить ще два додаткових запитання, на 3-й фазі – 5% за повною програмою з семи запитань.
Вибіркові оцінки кожної фази використовуються як додаткова інформація на наступних фазах, що підвищує точність результатів і є важливою властивістю багатофазної вибірки. Похибки багатоступінчастої та багатофазної вибірок розраховують окремо для кожного ступеня чи фази.
В практиці статистичного дослідження іноді доводиться зустрічатися з невеликими за обсягом так званими малими вибірками. Під малою вибіркою розуміють таке вибіркове спостереження, чисельність одиниць якого варіює в межах від 5 до 30. Хоча загальний принцип вибіркового обстеження (їз збільшенням обсягу вибірки підвищується точність вибіркових даних) лишається в силі, іноді доводиться обмежуватися малою кількістю спостережень. Часто така необхідність виникає при вибірковій перевірці якості продукції, в науково-дослідницькій роботі та в інших випадках.
Розробка теорії малої вибірки була розпочата англійським статистиком В. С. Госсетом, який друкувався під псевдонімом Стьюдент. Ним було доведено, що і при малих вибірках характеристики вибіркової сукупності можна застосовувати для оцінки параметрів генеральної сукупності, але за певних умов. Такими умовами є нормальний розподіл ознаки у генеральній сукупності. Для оцінки результатів малої вибірки та визначення можливих границь її випадкової помилки користуються критерієм Стьюдента (t). Однак це не означає, що можна використовувати малу вибірку тоді, колинеобхідна велика. В багатьох випадках розбіжності між знайденими межами можуть досягати значних розмірів, що навряд задовольнить дослідників. Тому малу вибірку слід застосовувати в статистичному дослідженні будь-яких явищ дуже обережно, з відповідним теоретичним та практичним обґрунтуванням. Необхідно також взяти до уваги і те, що точність результатів вибірки малого обсягу все ж нижча, ніж у великій вибірці.
3. Похибки вибірки. Визначення обсягу вибірки. Оцінка істотності вибіркових характеристик та способи поширення вибіркових даних
Між характеристиками вибіркової сукупності та шуканими характеристиками (параметрами) генеральної сукупності, як правило, існують деякі розбіжності, які називають помилками. Загальна величина можливої помилки вибіркової характеристики складається з помилок двоякого роду: помилки реєстрації і помилки репрезентативності.
Помилки реєстрації властиві будь-якому статистичному спостереженню взагалі.Порівняно з суцільними спостереженнями небезпека виникнення помилок реєстрації у вибіркових спостереженнях повинна бути меншою завдяки більш кваліфікованому і ретельному проведенню вибірки.
Помилки репрезентативності виникають від того, що вибірка не точно відтворюєсклад генеральної сукупності оскільки є випадковою величиною, тому і оцінки характеристик є випадковими величинами, які можуть не співпадати з відповідними параметрами генеральної сукупності.
За причинами виникнення помилки репрезентативності поділяються на систематичні та випадкові.
Систематичні (тенденційні) помилки репрезентативності виникають припорушенні принципу випадковості відбору (упереджений вибір елементів, недосконалий вибір одиниці відбору тощо). Систематичні помилки мають односторонній, тенденційний напрям і призводять до зсунення (викривлення) результатів обстеження в той чи інший бік. Їх ще визначають як помилки зміщення (зсунення). Наприклад: якщо для визначення середньої успішності потоку студентів взяти вибірку студентів, які сидять на останніх партах, то середня успішність вибірки буде меншою за середню успішність всього потоку. Якщо вибірку сформувати зі студентів, які сидять в перших рядах, то середня успішність у такій вибірці буде вищою від середньої успішності потоку. При такому нерівномірному відборі статистична оцінка успішності потоку буде заздалегідь занижена або завищена.
Систематичних помилок важливо уникати, оскільки незсуненість – одна з вимог до будь-якої вибіркової оцінки.
Випадкові помилки репрезентативності зумовлені тим, що розподіл відібраноїсукупності одиниць не досить точно відтворює розподіл одиниць генеральної сукупності.
На відміну від систематичних, випадкові помилки властиві вибірковому спостереженню та неминуче виникають і при додержанні принципу випадковості відбору. Але вони не носять тенденційного характеру і не ведуть до зміщення оцінок.
Випадкові помилки репрезентативності залежать від таких факторів:
- способу відбору;
- обсягу вибірки – обернено пропорційна залежність – чим більше одиницьвідібрано, тим менша помилка; але слід звернути увагу, що це стосується лише репрезентативної вибірки!, у випадку зсуненої – навпаки – збільшення її обсягу збільшує ймовірність отримати помилкові висновки;
- ступеня варіації досліджуваної ознаки у генеральній сукупності – прямазалежність – чим більша варіація ознаки, тим більша у середньому і помилка вибірки.
Визначення можливої і фактично допущеної помилки вибірки (випадкової) має велике значення при застосуванні вибіркового методу. Величина помилки характеризує ступінь надійності результатів вибірки, є необхідною для оцінки параметрів генеральної сукупності.
Для однієї конкретної вибірки можна визначити:
- середню та граничну помилки;
- ймовірність того, що похибка вибірки не перевищить допустимого рівня;
- обсяг вибірки, який забезпечить потрібну точність результатів для взятої ймовірності.
Середня (стандартна) похибка вибірки (m) – є середнім квадратичнимвідхиленням вибіркових оцінок від значення параметра в генеральній сукупності і обчислюється за формулою
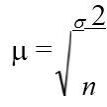
де s2 – генеральна дисперсія (на практиці замінюється вибірковою дисперсією – незсуненою оцінкою), а n – обсяг вибіркової сукупності. Отже, середня помилка вибірки для середньої величини збільшується із зростанням варіації генеральної сукупності і зменшується із збільшенням обсягу вибірки.
Для вирішення практичних завдань обчислення тільки середньої помилки вибірки недостатньо, тому визначають граничний для певної ймовірності розмір (інтервал) вибіркової помилки.
Гранична похибка вибірки (D) – це максимально можлива похибка для прийнятоїймовірності P і дорівнює t-кратному числу середніх помилок вибірки
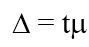
де t – коефіцієнт довіри. Гранична помилка надає можливість з′ясувати, у яких межах знаходиться величина генеральної середньої
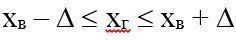
Значення ймовірності, з якою можна стверджувати, що помилка D не перевищує величини середньої помилки вибірки m для різних значень t обчислені та подані у спеціальних математичних таблицях. На практиці найчастіше використовують ймовірність 0,95 та 0,954 (відповідні їм величини t становлять 1,96 та 2,00).
Відбір вважається задовільним, якщо гранична помилка репрезентативності потрапляє у межі ± 2-5%.
Обсяг вибірки (n) визначають до проведення вибіркового спостереження,застосовуючи алгебраїчне перетворення формули граничної похибки вибірки, звідки
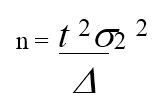
Отже достатній обсяг вибірки залежить від ступеня однорідності генеральної сукупності (s2), ймовірності, з якою гарантується результат (t2) і необхідної точності вибіркової оцінки (D2). На практиці ці значення встановлюють приблизно на підставі попередніх або аналогічних досліджень.
Наведені вище формули застосовують при простому випадковому та механічному відборі у разі повторної вибірки. Для інших видів відбору застосовують аналогічні формули з необхідними поправками на метод.
Для поширення вибіркових характеристик на генеральну сукупність необхідно спочатку оцінити результати спостереження з точки зору самої можливості поширення.
Істотність вибіркових середніх, часток і дисперсій можна оцінити методомстатистичної перевірки гіпотез, який надає можливість визначити ймовірність прийняття помилкового рішення на основі відповідних критеріїв (правил) узгодженості.
Для цього необхідно:
- сформулювати нульову гіпотезу Н0 – припущення про те, що вибіркова сукупність узгоджується з генеральною, і відповідну їй альтернативну гіпотезу Н1;
- обрати рівень істотності α (ймовірність ризику відхилення нульової гіпотези, найчастіше приймається рівним 0,05 або 0,01) та відповідне йому критичне значення – табульоване значення статистичної характеристики для ймовірності (1 – α);
- визначити область довірчих значень (при яких висунута гіпотеза Н0 приймається) за відповідними формулами критеріальних статистик та критичну область (при яких нульова гіпотеза відхиляється);
- прийняти те чи інше рішення на основі порівняння фактичного та критичного (табличного) значень критерію. При нормальному розподілі ознаки у генеральній сукупності використовують таблиці Лапласа.
Отже якщо вибіркові дані суперечать гіпотезі Н0 (фактичне значення критерію перевищує критичне), вона відхиляється. Коли ці дані узгоджуються з гіпотезою Н0, вона приймається і результати вибіркового спостереження можна поширити на генеральну сукупність.
Існує декілька способів поширення вибіркових даних:
- спосіб прямого розрахунку – полягає у визначенні показників обсягу генеральної сукупності: середній розмір ознаки, обчислений в результаті вибіркового спостереження, треба помножити на чисельність одиниць генеральної сукупності;
- метод поправочних коефіцієнтів – застосовують тоді, коли вибіркове спостереження проводять з метою перевірки та уточнення результатів суцільного спостереження: дані суцільного та вибіркового спостережень зіставляють і обчислюють поправочні коефіцієнти.
Важливе зауваження: публікуючи будь-де статистичні дані, які обчислені наоснові вибірки, обов′язково слід пояснювати, що відповідні показники отримані розрахунковим способом на базі матеріалів вибіркового спостереження!









