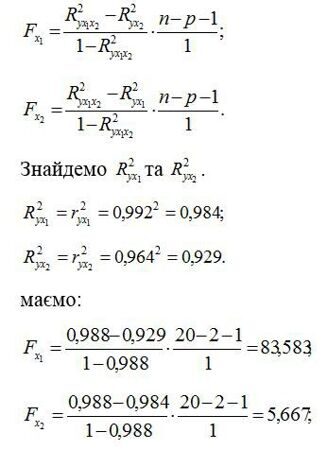Розрахункова робота з курсу Економетрика - 4 задачі

« Назад

Задача 1

По територіях регіону приводяться дані за 200Х рік (див. таблицю свого варіанту).

Необхідно:

1. Графічно зобразити залежність між двома змінними та зробити висновок щодо можливості побудови лінійної парної моделі.

2. Побудувати лінійне рівняння парної регресії y від х.

3. Розрахувати лінійний коефіцієнт кореляції, коефіцієнт детермінації та коефіцієнт еластичності. Зробити відповідні висновки.

4. Оцінити статистичну значимість параметрів регресії і кореляції за допомогою F-критерію Фішера та t-критерію Ст’юдента.

5. Виконати прогноз заробітної плати у при прогнозному значенні середньодушового прожиткового мінімуму х, що складає 107% від середнього рівня.

6. Оцінити точність прогнозу, розрахувавши похибку прогнозу і його довірчий інтервал.

Розв’язок

1. Будуємо графічно залежність середньоденної заробітної плати від середньодушового прожиткового мінімуму, відкладаючи значення незалежної змінної по осі Х, залежної – по осі Y.

Рисунок дозволяє зробити висновок про наявність прямої залежності між середньоденною заробітною платою та середньодушовим прожитковим мінімумом. Очевидно, що така залежність може бути описана рівнянням простої лінійної регресії.

2. Для розрахунків параметрів рівняння лінійної регресії будуємо розрахункову таблицю.

Розрахункова таблиця

Знаходимо оцінки параметрів рівняння регресії:

Отримане рівняння регресії: .

Із збільшенням середньодушового прожиткового мінімуму на 1 грн. середньоденна заробітна плата зростає в середньому на 0,96 грн.

3. Тісноту лінійного зв’язку можна оцінити за допомогою коефіцієнта кореляції:

Оскільки значення коефіцієнта кореляції більше 0,6, то це говорить про наявність достатньо тісного лінійного зв’язку між ознаками.

Коефіцієнт детермінації:

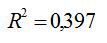
Це означає, що 39,7% варіації заробітної плати (у) пояснюється варіацією фактору х – середньодушового прожиткового мінімуму.

Коефіцієнт еластичності:

Коефіцієнт показує, що із зміною х на 1% у зміниться в середньому на 0,6%. Зв’язок нееластичний.

4. Оцінку значимості рівняння регресії в цілому проведемо за допомогою F-критерію Фішера. Фактичне значення F-критерію:

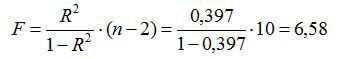
Табличне значення F-критерію при 5%-му рівні значимості і ступенях вільності p=1, n-p-1=12-1-1=10 складає F_табл = 4,96. Оскільки F_факт<F_табл, то рівняння регресії можна визнати статистично не значимим, а модель – не адекватною.

Оцінку статистичної значимості параметрів регресії проведемо за допомогою t-тесту Ст’юдента і шляхом розрахунку довірчого інтервалу кожного з показників.

Табличне значення t-критерію для кількості ступенів вільності df=n-2=12-2=10 та α=0,05 складе t_табл=2,23.

Визначимо випадкові похибки m_a, m_b, m_r (залишкова дисперсія на один ступінь вільності 

Тоді

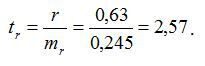
Фактичні значення t-статистики перевищують табличні значення: t_a<t_табл; t_b>t_табл; t_r>t_табл. Тому параметри a, b і коефіцієнт кореляції r не випадково відрізняються від нуля, а є статистично значимими.

Розрахуємо довірчі інтервали для параметрів регресії a та b. Для цього визначимо граничну похибку для кожного показника:

Δ_a=t_табл∙m_a=2,23∙31,98=71,32

Δ_b=t_табл∙m_b=2,23∙0,369=0,823.

Довірчі інтервали складають:

a±Δ_a=55,38±71,32 i -15,94 ≤ a ≤ 126,69

b±Δ_b=0,96±0,823 i 0,137 ≤ b ≤ 1,782

Аналіз верхньої та нижньої границь довірчих інтервалів приводить до висновку про те, що з імовірністю 95% параметри a і b, що знаходяться у вказаних границях, не приймають нульових значень, тобто є статистично значимими і відмінними від нуля.

5. Отримані оцінки рівняння регресії дозволять використати його для прогнозу. Якщо прогнозне значення прожиткового мінімуму складе  грн., тоді точковий прогноз заробітної плати складе:

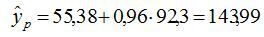 грн.

6. Помилка прогнозу складає:

Гранична похибка прогнозу, яка в 95% випадків не буде перевищена, складе:

Δ_у = t_табл∙m_ŷ = 161,29±7,39 і 127,51≤y*≤160,47.

Виконаний прогноз середньоденної заробітної плати є надійним (95%) і знаходиться у межах від 127,51 до 160,47 грн.

Задача 2

По 20 підприємствах регіону досліджується залежність виробки продукції на одного робітника у (тис. грн.) від введення в дію нових основних фондів х₁ (% від вартості фондів на кінець року) і від питомої ваги робочих високої кваліфікації в загальній чисельності робочих х₂ (%).

Номер підприємства	у	х1	х2	Номер підприємства	у	х1	х2
1	7	3,5	9	11	10	6,3	21
2	7	3,6	10	12	10	6,8	22
3	7	3,8	14	13	11	7,2	24
4	7	4,2	15	14	12	7,9	25
5	8	4,3	18	15	12	8,1	26
6	8	4,7	19	16	13	8,3	29
7	9	5,4	19	17	13	8,4	31
8	9	5,6	20	18	13	8,8	32
9	10	5,9	20	19	14	9,6	35
10	10	6,1	21	20	14	9.7	36

Необхідно:

1. Побудувати лінійну модель множинної регресії. Записати стандартизоване рівняння множинної регресії. На основі стандартизованих коефіцієнтів регресії і середніх коефіцієнтів еластичності ранжувати фактори за ступенем їх впливу на результат.

2. Знайти коефіцієнти парної, часткової та множинної кореляції. Проаналізувати їх.

3. Знайти скоригований коефіцієнт коефіцієнт множинної детермінації. Порівняти його з не коригованим (загальним) коефіцієнтом детермінації.

4. За допомогою F-критерію Фішера оцінити статистичну надійність рівняння регресії і коефіцієнта детермінації.

5. За допомогою часткових F-критеріїв фішера оцінити доцільність включення в рівняння множинної регресії фактору х1 після х2 і фактору х1 після х2.

6. Скласти рівняння лінійної парної регресії, залишивши лише один значимий фактор.

Розв’язок

Для зручності проведення розрахунків помістимо результати обчислень у таблицю.

Знайдемо середньоквадратичні відхилення ознак:

1. Обчислення параметрів лінійного рівняння множинної регресії.

Для знаходження параметрів лінійного рівняння множинної регресії

необхідно розв’язати таку систему лінійних рівнянь відносно невідомих параметрів a, b₁, b₂:

або скористатися готовими формулами:

Розрахуємо спочатку парні коефіцієнти кореляції

Знаходимо

Таким чином, отримане рівняння множинної регресії:

Коефіцієнти β₁ та β₂ стандартизованого рівняння регресії t_y=β₁t_x1+β₂t_x2+ε, знаходяться по формулах:

Тобто рівняння буде виглядати таким чином:

Оскільки стандартизовані коефіцієнти регресії можна порівнювати між собою, то можна сказати, що введення в дію нових основних фондів спричиняє великий вплив на виробку продукції, ніж питома вага робітників високої кваліфікації.

Порівняти вплив факторів на результат можна також за допомогою середніх коефіцієнтів еластичності:

Обчислюємо:

Тобто збільшення тільки основних фондів (від свого середнього значення) або тільки питомої ваги робітників високої кваліфікації на 1% у першому випадку збільшує в середньому виробіток продукції на 0,756% або зменшує у другому випадку на -0,003% відповідно. Таким чином, підтверджується більший вплив на результат у фактора х₁, ніж фактора х₂.

2. Коефіцієнти кореляції вже знайдені:

Вони вказують на досить сильний зв’язок кожного фактора з результатом, а також високу міжфакторну залежність (фактори х₁ та х₂ явно колінеарні, оскільки r>0,7). За такої сильної міжфакторної залежності рекомендується один з факторів виключити з розгляду.

Часткові коефіцієнти кореляції характеризують тісноту зв’язку між результатом і відповідним фактором при елімінуванні (усуненні впливу) інших факторів, що включені в рівняння регресії.

При двох факторах часткові коефіцієнти кореляції розраховуються таким чином:

Якщо порівняти коефіцієнти парної та часткової кореляції, то можна побачити, що через високу між факторну залежність коефіцієнти парної кореляції дають завищені оцінки тісноти зв’язку. Саме по цій причині рекомендується за наявності сильної колінеарності (взаємозв’язку) факторів виключати з дослідження той фактор, у якого тіснота парної залежності менше, ніж тіснота міжфакторного зв’язку.

Коефіцієнт множинної кореляції визначити через матрицю парних коефіцієнтів кореляції:

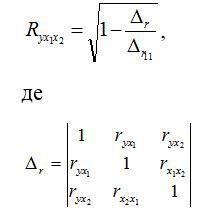
- визначник матриці парних коефіцієнтів кореляції;

- визначник матриці міжфакторної кореляції.

Коефіцієнт множинної кореляції:

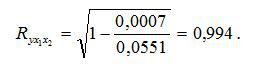
Коефіцієнт множинної кореляції показує на досить сильний зв’язок всього набору факторів з результатом.

3. Нескоригований коефіцієнт множинної детермінації складає  і оцінює частку варіації результату за рахунок представлених в рівнянні факторів в загальній варіації результату. Тут ця частка складає 99,4% і вказує на досить високий ступінь обумовленості варіації результату варіацією факторів, іншими словами – на досить тісний зв’язок факторів з результатом.

Скоригований коефіцієнт множинної детермінації обчислюється за формулою:

Скоригований коефіцієнт детермінації визначає тісноту зв’язку з урахуванням ступенів вільності загальної і залишкової дисперсій. Він дає таку оцінку тісноти зв’язку, яка не залежить від числа факторів і тому не може порівнюватися по різних моделях з різною кількістю факторів. Обидва коефіцієнта вказують на досить високу (більше 98%) детермінованість результату у в моделі факторами х₁ та х₂.

4. Оцінку надійності рівняння регресії в цілому і показника тісноти зв’язку  дасть F-критерій Фішера:

В нашому випадку фактичне значення F-критерію Фішера складає:

Отримали, що F_факт>F_табл = 3,49 (при n=20), тобто ймовірність випадково отримати таке значення F-критерію не перевищує допустимий рівень значимості 5%. Відповідно, отримане значення не випадкове, воно сформувалося під впливом суттєвих факторів, тобто підтверджується статистична значимість всього рівняння і показника тісноти зв’язку .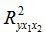

5. За допомогою часткових F-критеріїв Фішера оцінимо доцільність включення в рівняння множинної регресії фактора х₁ після х₂ і фактора х₂ після х₁ за допомогою формул:

Отримали, що < F_табл = 3,49. Відповідно, включення в модель фактору х₂ після того, як в модель включений фактор х₁ статистично недоцільно: приріст факторної дисперсії за рахунок додаткової ознаки х₂ виявляється незначним, несуттєвим; фактор х₂ включати в рівняння після фактору х₁ не варто.

Якщо змінити початковий порядок включення факторів в модель і розглянути варіант включення х₁ після х₂, то результат розрахунку часткового F-критерію для х₁ буде іншим. F₁>F_табл=3,49, тобто ймовірність його випадкового формування менше прийнятого стандарту α=0,05 (5%). Відповідно, значення часткового F-критерію для додатково включеного фактору х₁ не випадкове, є статистично значимим, надійним, достовірним: приріст факторної дисперсії за рахунок додаткового фактору х₁ є суттєвим. Фактор х₁ повинен бути присутнім в рівнянні, в тому числі в варіанті, коли він включається після фактору х₂.

6. Загальний висновок полягає в тому, що множинна модель з факторами х₁ та х₂ з  містить неінформативний фактор х₂. Якщо виключити фактор х₂, то можна обмежитися рівнянням парної регресії:

 

Задача 3

Є умовні дані про споживання електроенергії (у_t) жителями регіону за 16 кварталів.

Необхідно:

1. Побудувати автокореляційну функцію і зробити висновок про наявність сезонних коливань.

2. Побудувати адитивну модель часового ряду.

3. Зробити прогноз на 2 квартали уперед.

Розв’язок

Для зручності проведення розрахунків помістимо результати обчислень у таблицю.

Розрахунок коефіцієнта автокореляції першого порядку

Визначимо коефіцієнт кореляції між рядами y_t та y_t-1 та виміряємо тісноту зв’язку між споживанням електроенергії поточного і попереднього років. Додаємо зсунутий на один період часу часовий ряд y_t-1.

Одна з робочих формул для розрахунку коефіцієнта кореляції має вигляд:

Для автокореляції рівнів ряду першого порядку коефіцієнт кореляції матиме вигляд:

Скориставшись формулою коефіцієнта кореляції отримаємо коефіцієнт автокореляції рівнів першого порядку:

Отримане значення свідчить про незначну залежність між споживанням електроенергії поточного і безпосередньо попереднього років, і відповідно, про наявність в часовому ряді споживання електроенергії слабкої лінійної тенденції.

Кількість періодів, за яким розраховується коефіцієнт автокореляції, називається лагом. Із збільшенням лагу кількість пар значень, за якими розраховується коефіцієнт автокореляції, зменшується. Деякі автори вважають доцільним для забезпечення статистичної достовірності коефіцієнтів автокореляції використовувати правило „максимальний лаг повинен бути не більше n/4”.

Послідовність коефіцієнтів автокореляції рівнів першого, другого і т.д. порядків називають автокореляційною функцією часового ряду. Графік залежності її значень від величини лагу (порядку коефіцієнту кореляції) називають корелограмою.

Зведена таблиця коефіцієнта автокориляції

Аналіз значень авто кореляційної функції дозволяє зробити висновок про наявність у часовому ряді, що вивчається, по-перше, лінійної тенденції, по-друге, сезонних коливань періодичністю в 4 квартали.

Рис. 3 - Коефіцієнт автокориляції рівнів

Відомо декілька підходів до аналізу структури часових рядів, що містять сезонні або циклічні коливання.

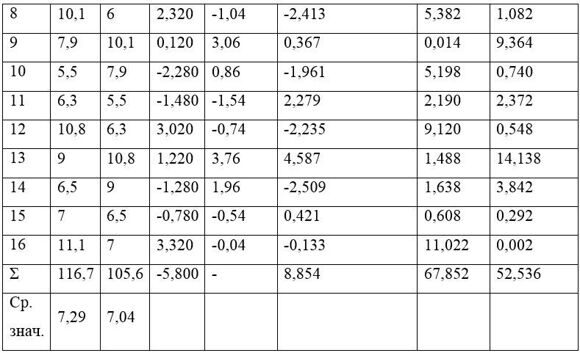
Проведемо вирівнювання вихідних рівнів ряду методом ковзної середньої. Для цього розраховуємо ковзну середню за 4 квартали, центровану ковзну середню.

Номер кварталу, t	Споживання електроенергії, yt	Всього за 4 квартали	Ковзна середня за 4 квартали	Центрована ковзна середня	Оцінка сезонної компоненти	Квадрат відхилення від серднього
1	5,8	-	-	-	-	2,231
2	4,5	24,500	6,125	-	-	7,805
3	5,1	25,700	6,425	6,275	-1,175	4,813
4	9,1	26,200	6,550	6,488	2,613	3,263
5	7	27,100	6,775	6,663	0,338	0,086
6	5	28,100	7,025	6,900	-1,900	5,261
7	6	29,000	7,250	7,138	-1,138	1,674
8	10,1	29,500	7,375	7,313	2,788	7,875
9	7,9	29,800	7,450	7,413	0,488	0,368
10	5,5	30,500	7,625	7,538	-2,038	3,218
11	6,3	31,600	7,900	7,763	-1,463	0,988
12	10,8	32,600	8,150	8,025	2,775	12,294
13	9	33,300	8,325	8,238	0,762	2,911
14	6,5	33,600	8,400	8,363	-1,863	0,630
15	7	-	-	-	-	0,086
16	11,1	-	-	-	-	14,488
Ср. знач.	7,294	-	-	-	Сума	67,989

Даний ряд містить сезонні коливання періодичністю 4. По графіку ряду можна встановити наявність приблизно рівної амплітуди коливань. Це свідчить про відповідність ряду адитивній моделі. Розрахуємо її компоненти.

Рис. 4 - Споживання електроенергії

Знайдемо оцінки сезонної компоненти як різницю між фактичними рівнями ряду і центрованими ковзними середніми. Використовуємо ці оцінки для розрахунку значень сезонної компоненти S. В моделях існує припущення, що сезонні дії за період взаємопогашаються. В адитивній моделі це виражається в тому, що сума значень сезонної компоненти по всіх кварталах повинна дорівнювати нулю.

Для даної моделі маємо: 0,529-1,933-1,258+2,725=1,063

Визначимо коригуючий коефіцієнт:

k=1,063/4=0,26575

Розрахуємо скориговані значення сезонної компоненти як різницю між її середньою оцінкою і коригуючим коефіцієнтом k:

де і = 1: 4.

Перевіримо рівність нулеві суми значень сезонної компоненти:

0,514-1,949-1,274+2,709=0

Таким чином, отримано такі значення сезонної компоненти:

І квартал: S₁ = 0,514

II квартал: S₂ = -1,949

III квартал: S₃ = -1,274

IV квартал: S₄ = 2,709

Занесемо ці значення в таблицю для відповідних кварталів.

Елімінуємо вплив сезонної компоненти, вираховуючи її значення з кожного рівня вихідного часового ряду. Отримуємо: T + E = Y – S. Ці значення розраховуються для кожного моменту часу і містять тільки тенденцію та випадкову компоненту.

Номер кварталу, t	Споживання електроенергії, yt	Si	T+E=yt-Si	T	T+S	E=yt-(T+S)	E2
1	5,8	0,514	5,286	5,895	6,409	-0,609	0,37
2	4,5	-1,949	6,449	0,373	-1,576	6,076	36,92
3	5,1	-1,274	6,374	0,560	-0,714	5,814	33,81
4	9,1	2,709	6,391	0,746	3,455	5,645	31,86
5	7	0,514	6,486	0,933	1,447	5,553	30,84
6	5	-1,949	6,949	1,119	-0,830	5,830	33,98
7	6	-1,274	7,274	1,306	0,032	5,968	35,62
8	10,1	2,709	7,391	1,492	4,201	5,899	34,79
9	7,9	0,514	7,386	1,679	2,193	5,707	32,57
10	5,5	-1,949	7,449	1,866	-0,083	5,583	31,17
11	6,3	-1,274	7,574	2,052	0,778	5,522	30,49
12	10,8	2,709	8,091	2,239	4,948	5,852	34,25
13	9	0,514	8,486	2,425	2,939	6,061	36,73
14	6,5	-1,949	8,449	2,612	0,663	5,837	34,07
15	7	-1,274	8,274	2,798	1,524	5,476	29,98
16	11,1	2,709	8,391	2,985	5,694	5,406	29,23
Сума							496,7
Прогноз
17				3,234	3,748
18				3,220	1,271

Визначимо компоненту Т даної моделі. Для цього проведемо аналітичне вирівнювання ряду (Т+Е) за допомогою лінійного тренду. Результати аналітичного вирівнювання (побудови регресії (Т+Е) в залежності від t):

Т=5,708+0,186·t

Підставивши в рівняння значення t знаходимо рівні Т для кожного моменту часу.

Знайдемо значення рівнів ряду, отримані за адитивною моделлю. Для цього додамо до рівнів Т значення сезонної компоненти для відповідних кварталів.

У відповідності до методики побудови адитивної моделі розрахунок похибки проводиться за формулою

Е = Y – (T + S).

Це абсолютна похибка.

За аналогією з моделлю регресії для оцінки якості побудови моделі, а також для вибору найкращої моделі можна використовувати суму квадратів абсолютних помилок. Для даної моделі сума квадратів абсолютних помилок дорівнює 1,10. По відношенню до загальної суми квадратів відхилень рівнів ряду від його середнього рівня, рівної 67,989, ця величина складає трохи більше 1,5%:

(1-1,10/67,989)·100 = 98,4

Відповідно, можна сказати, що адитивна модель пояснює 98,4% загальної варіації рівнів часового ряду споживання електроенергії за останні 16 кварталів. 

Задача 4

Дано систему економетричних рівнянь.

Модифікована модель Кейнса:

де С – споживання; Y – дохід; І – валові інвестиції; G – державні витрати; t – поточний період; t-1 – попередній період.

Необхідно:

1. Застосувавши необхідну та достатню умову ідентифікації, визначте, чи ідентифікується кожне з рівнянь моделі.

2. Визначте метод оцінки параметрів моделі.

3. Запишіть в загальному вигляді приведену форму моделі.

Розв’язок

У цій моделі три ендогенні змінні (C_t, T, Y_t). Причому змінна Y_t задана тотожністю. Тому практично статистичне рішення необхідно тільки для перших двох рівнянь системи, які необхідно перевірити на ідентифікацію. Модель містить дві зумовлені змінні - екзогенну G_t і лагів - Y_t-1.

При практичному вирішенні задачі на основі статистичної інформації за ряд років або за сукупністю регіонів за один рік в рівняннях для ендогенних змінних C_t, I_t зазвичай міститься вільний член (а₁, а₂), значення якого акумулює вплив неврахованих в рівнянні факторів і не впливає на визначення ідентифікованості моделі.

Оскільки фактичні дані про ендогенні змінні C_t, I_t можуть відрізнятися від постуліруемих моделлю, то прийнято в модель включати випадкову складову для кожного рівняння системи, виключивши тотожності. Випадкові складові позначені через ɛ₁ і ε₂. Вони не впливають на вирішення питання про ідентифікацію моделі.

У досліджувальній економетричній моделі в першому рівнянні системи дві ендогенні змінні C_t, I_t, тобто H = 2, число відсутніх зумовлених змінних також дорівнює двом (G_t і Y_t-1) - D = 2.

За розрахунковим правилом: D + 1> H, тобто 2 + 1> 2.

Отже, рівняння понадідентифіковане.

Коефіцієнти при відсутніх в першому рівнянні змінних складуть:

Згідно таблиці detA ≠ 0, ранг матриці дорівнює двом, що відповідає наступному критерію: ранг матриці коефіцієнтів повинен бути не менше ніж число ендогенних змінних в системі без одного. Достатня умова ідентифікації виконується.

У другому рівнянні системи дві ендогенних змінних Y_t, I_t, тобто H = 2, число відсутніх зумовлених змінних дорівнює одному (G_t) - D = 1.

За розрахунковим правилом D + 1 = H, тобто 1 + 1 = 2.

Отже, рівняння ідентифіковане.

Коефіцієнти при відсутніх в другому рівнянні змінних складуть:

Згідно таблиці detA ≠ 0, ранг матриці дорівнює двом. Достатня умова ідентифікації виконується.

Тотожність не вимагає перевірки на ідентифікацію.

Так як модель містить хоча б одне понадідентифіковане рівняння, отже, в цілому вона понадідентифіковане.

Для визначення параметрів понадідентифікованої моделі використовується двох кроковий метод найменших квадратів.

Запишемо наведену форму моделі в загальному вигляді:

де, u₁, u₂ та u₃ – випадкові помилки.