Лекція №5, Закон великих чисел

« Назад

Вступ

Теорія ймовірностей вивчає закономірності, властиві масовим випадковим явищам. Закономірності виявляються при великій кількості випадкових явищ, що відбуваються при однакових умовах.

Це означає, що характеристики випадкових подій і випадкових величин в цих умовах стають стійкими: середній їх результат (наприклад, частота події, середні значення випадкової величини) перестає бути випадковим і може бути передбачений з великим ступенем визначеності. Вказана особливість є суттю “закону великих чисел”.

Розглянемо групу теорем, що присвячені граничним законам розподілу. Нехай ξ випадкова величина з математичним сподіванням Ì ξ та дисперсією Dξ.

В подальшому при доведенні теорем будемо користуватись нерівністю Чебишова, що доведена в теоремі 1.

Теорема 1. Ймовірность того, що відхилення випадкової величини від її математичного сподівання за абсолютною величиною не менше будь-якого додатного числа ε, що не перевищує:

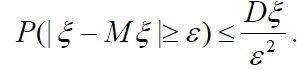
Доведення. Нехай ξ – неперервна в. в. із щільністю розподілу (х). Тоді:

.

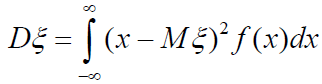Позначимо АВ: |ξ −Mξ |<ε. Виділимо на числовій осі праворуч і ліворуч від математичного сподівання Mξ відрізки, кожен довжиною ε. Якщо у виразі для Dξ інтеграл по всій осі 0х замінити інтегралом по області, який лежить зовні відрізка AB, то, оскільки під інтегралом знаходиться невід’ємна функція, величина інтеграла може тільки зменшитися, тобто:

.

Замінюючи | õ − Mξ | під знаком інтеграла на ε, ми знову можемо тільки зменшити величину інтеграла:

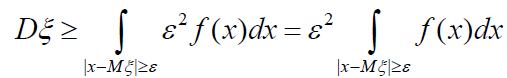
Інтеграл в правій частині визначає ймовірність того, що випадкова величина ξ прийме значення, яке знаходяться за межами відрізка АВ:

.

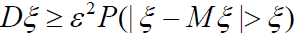Звідки:

.

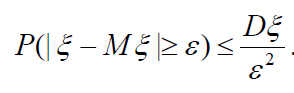Нерівність Чебишова може бути записана в іншій формі, для протилежної події. Імовірність абсолютної величини відхилення в. в. від математичного сподівання, менша ε, визначається за формулою:

.

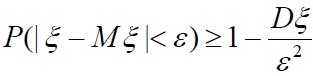Зауваження. Нерівність Чебишова має для практики обмежене значення, оскільки часто дає грубу оцінку.

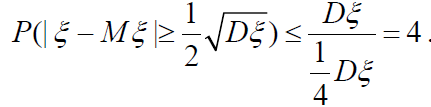
Зрозуміло, що жодна йвомірність не може бути більшою не тільки чотирьох, але навіть одиниці. Якщо, наприклад ε =10 Dξ, то: Це вже непогана оцінка імовірності.

Таким чином, бачимо, що нерівність Чебишова корисна лише при відносно великих ε.

Теоретичне значення нерівності Чебишова дуже велике. Нижче ми скористаємось цією нерівністю при доведенні теореми Чебишова.

Приклад. Дано випадкову величину ξ з математичним сподіванням Mξ і дисперсією (σξ )2. Оцінити зверху ймовірність того, що в. в. ξ відхилиться від свого математичного сподівання не менше, ніж на 3σξ.

Розв’язання. Вважаючи в нерівності Чебишова ε = 3σ, одержимо:

.

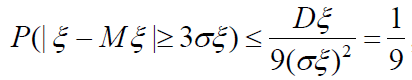Імовірність того, що відхилення випадкової величини від її математичного сподівання вийде за межі трьох середніх квадратичних відхилень, не може бути більша 1 0,11(1) 9 ≈.

Нерівність Чебишова дає тільки верхню границю імовірності даного відхилення. Вище цієї межі ймовірність не може бути.

В більшості випадків імовірність того, що величина ξ вийде за межі відрізка M ± 3σξ, значно менша 19.

Наприклад, для нормального закону ця ймовірність дорівнює 0,003. На практиці найчастіше ми маємо справу з випадковими величинами, значення яких дуже рідко виходять за межі Mξ ± 3σξ.

Якщо закон розподілу випадкової величини невідомий, а відомі тільки Mξ і σξ, відрізок (Mξ − 3σξ ; Mξ + 3σξ ) вважають відрізком практично можливих значень випадкової величини (так зване правило “трьох сігм”).