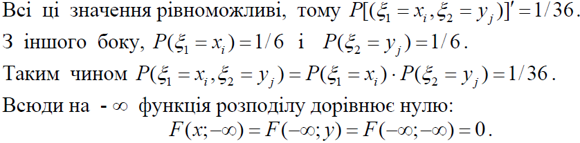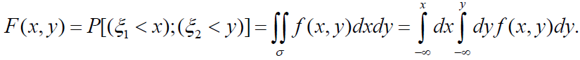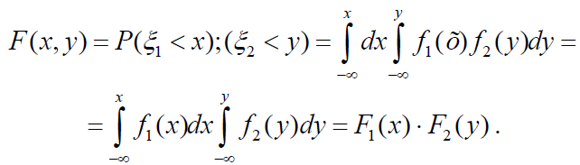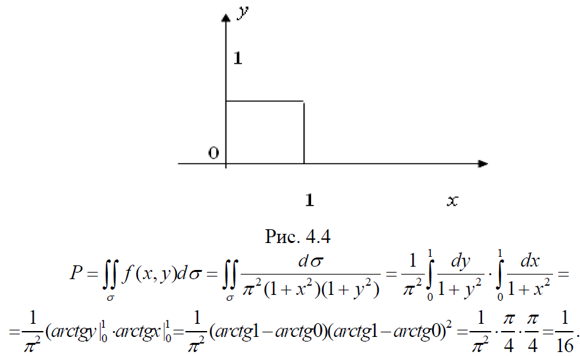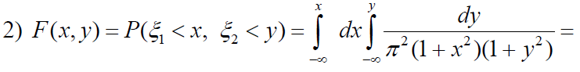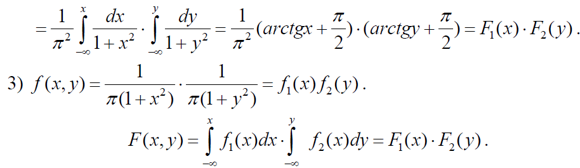Лекція №4, Двовимірні випадкові величини

« Назад

Вступ

Часто потрібно розв’язувати задачі, в яких розглядаються події, що описуються не однією, а декількома, зокрема, двома випадковими величинами. Так, якщо станок-автомат штампує цілиндричні валики, то діаметр валика ξ1 і його висота ξ2 утворюють систему двох випадкових величин (ξ1, ξ2).

Двовимірною випадковою величиною (two-dimensional random variable) називають систему двох випадкових величин (ξ1, ξ2), для яких визначена імовірність P(ξ1,<x, ξ2<y) одночасного виконання нерівностей ξ1,<x та ξ2<y, де х і у – довільні дійсні числа. Систему двох випадкових величин (ξ1, ξ2) можна показати випадковою точкою в декартовій системі координат (х, у).

Функція двох змінних F(х,у)=P(ξ1,<x, ξ2<y), визначена для довільних х і у, називається функцією розподілу величин (ξ1, ξ2).

Функція розподілу (distribution function) - це імовірність попадання випадкової точки (ξ1, ξ2) в “нескінченний квадрат” з вершиною в точці (х, у), що знаходиться лівіше і нижче вертикального та горизонтального обмежень.

Сформулюємо властивості функції розподілу системи двох випадкових величин.

1. Функція розподілу F(х,у) є функція неспадна. Тобто при х2>x1, F(х2,у) ≥ F(х1,у), при у2 > у1, F(х,у2) ≥ F(х,у1).

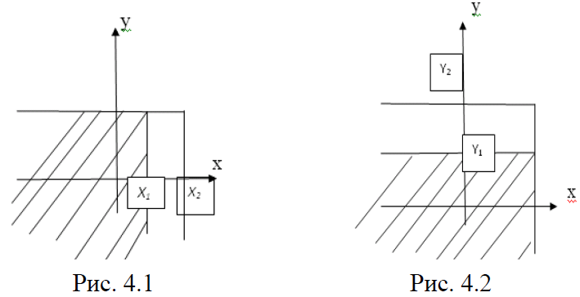
В цій властивості F(х,у) можна переконатись, використовуючи геометричну інтерпретацію функції розподілу як ймовірності попадання в “квадрат” з вершиною (х,у). Дійсно, збільшуючи х, (зміщуючи праву границю “квадрата” вправо (рис. 4.1) або збільшуючи у (зміщуючи верхню границю вгору (рис. 4.2), ми не можемо зменшити імовірність попадання в цей “квадрат”. Двовимірна випадкова величина (ξ1, ξ2) називається дискретною, якщо ξ1, ξ2 - дискретні величини.

Нехай будь-які можливі значення ξ1, ξ2 утворюють кінцеві послідовності х1, х2, х3 … хn і у1, у2, у3, ... уs.. Можливі значення величини (ξ1, ξ2) мають вигляд (хi,yj), де i – 1, 2, 3, n, j – 1, 2, 3, … s. Позначимо через pijімовірність того, що (ξ1, ξ2) = (хi,yj), pij =P(ξ1,=xі),(ξ2=yj), функція розподілу має вигляд ( , ) =Σi Σj ij F x y p , де подвійна сума поширена на i та j, для яких хi < х, уj< у. Двовимірну випадкову величину (ξ1, ξ2), як і одновимірну, можна задавати таблицею, яка називається її законом розподілу. В першому рядку вказані значення, яких набуває величина ξ1, а в першому стовпці – величина ξ2. В інших клітинках таблиці вказано відповідні ймовірності, причому їх сума завжди дорівнює одиниці.

Розглянемо, наприклад, двовимірну випадкову величину, задану такою таблицею:

Сума всіх ймовірностей:

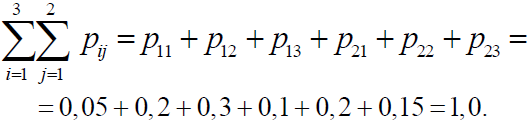
Дві дискретні випадкові величини ξ1 і ξ2 називаються незалежними, якщо для всіх пар i та j виконуються співвідношення:

Приклад 1. Два гральних кубика кидають по одному разу. Позначимо через ξ1 число очок, які випали на першому кубику, а через ξ2 – на другому, тоді (ξ1, ξ2) – двовимірна дискретна величина. Покажемо, що величини ξ1 та ξ2 незалежні. Оскільки кожна із величин ξ1, ξ2 незалежно одна від одної може приймати 6 різних значень, то число різних значень двовимірної випадкової величини (ξ1, ξ2) рівне 36.

В цій властивості ми переконуємось, спостерігаючи, що при необмеженому посуванні вліво правої границі квадрата (x→−∞) чи вниз його верхньої границі (y→−∞), або рухаючи одочасно обома границями, імовірність попадання у відповідний квадрат прямуватиме до нуля.

Коли один з аргументів дорівнює +∞, функція розподілу системи перетворюється в функцію розподілу випадкової величини, яка відповідає другому аргументу:

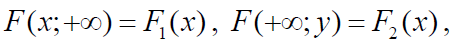
де F1(x) , 2F (x) - відповідно, функції розподілу випадкових величин ξ1 і ξ2.

Якщо обидва аргументи дорівнюють +∞, функція розподілу системи дорівнює одиниці: F(+∞;+∞) =1.

Дійсно, при x → +∞, y→+∞ “квадрат” з вершиною (x, y) переходить на всю площину хOу, попадання в яку є вірогідна подія.

Основне питання для системи двох випадкових величин є питання про ймовірність попадання випадкової точки (ξ1, ξ2) в межі заданої області D на площині хОу.

Імовірність попадання випадкової точки в задану область виражається найбільш просто в тому випадку, коли ця область являє собою прямокутник зі сторонами, паралельними осям координат. Виразимо через функцію розподілу ймовірність попадання випадкової точки (ξ1, ξ2) в прямокутник R, обмежений абсцисами α і β та ординатами γ і δ (рис. 4. 3).

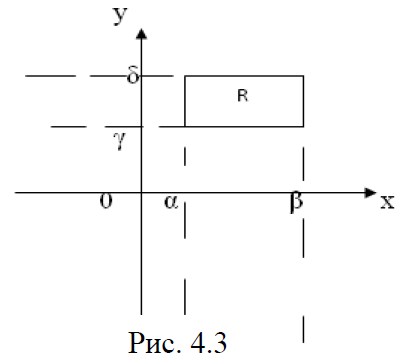
Далі визначимо формулу для ймовірності попадання випадкової точки в область довільної форми.

Двовимірна величина (ξ1, ξ1) називається неперервною, якщо існує така неперервна невід’ємна функція f(x, y) двох змінних, що ймовірність попадання випадкової точки М(ξ1, ξ1) в деяку область σ площини хОу дорівнює подвійному інтегралу від функції f(x, y) по області σ:

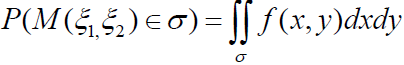
Функція f(x, y) називається щільністю розподілу імовірності системи двох випадкових величин ξ1, ξ2. Тоді функцію розподілу системи випадкових величин можна записати так:

Графічно f(x, y) - поверхня розподілу. Неперервні випадкові величини ξ1, ξ2 називаються незалежними, якщо f(x, y) = f1(x) f2(y), де f1(x) і f2(y) – відповідно, щільності розподілу імовірності випадкових величин ξ1 і ξ2. В цьому випадку:

де F1(x) і F2(y) - відповідно, функції розподілу величин ξ1, ξ1.

Приклад 2. Двовимірна випадкова величина (ξ1, ξ1) має щільність розподілу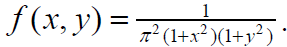 

Знайти:

1) Імовірність попадання випадкової точки 1 2 M(ξ, ξ) в квадрат:

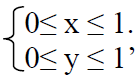
2) Функцію розподілу F(x,y);

3) Щільності і функції розподілу кожної з величин 1 2 ξ, ξ окремо.

Розв’язання.

1) Імовірність Р попадання випадкової точки М( 1 2 ξ, ξ) в квадрат, зображений на рисунку (рис. 4.4), дорівнює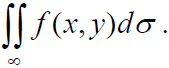 

Можна переконатися, що виконується рівність.

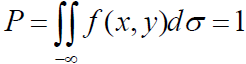
Для неперервних випадкових величин важливими характеристиками є дві функції розподілу: F(x, y) - функція розподілу, f (x, y) – щільність розподілу.