Лекция Динамика машин

« Назад

1. Основные задачи и законы динамики

Динамикой называется раздел механики, изучающий зависимость между механическим движением тел и действующими на них силами.

Всякое механическое движение тела рассматривается в динамике в связи с физическими факторами, определяющими характер этого движения. В этом отличие динамики от кинематики, где движение рассматривается только с геометрической стороны.

Множество частных задач динамики можно разбить на две основные группы, свести к двум основным задачам.

Первая задача динамики. Известно движение данной материальной точки или данной системы.

Требуется определить силы, действующие на эту точку или эту систему.

Вторая задача динамики (обратная первой). Известны силы, действующие на данную материальную точку или данную систему. Требуется определить движение этой точки или этой системы.

Для установления связи между движением материальных тел и факторами, определяющими его характер в динамике пользуются рядом физических понятий (масса, количество движения, работа, энергия и т. д.). Количественные соотношения между различными физическими величинами, связанными с механическим движением материальных тел, устанавливаются в динамике путем математических выводов из основных законов классической механики. Эти законы служат фундаментом, на котором строится все содержание динамики.

Первый закон (закон инерции): всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействия со стороны других тел не заставят его изменить это состояние.

Применяя законы классической динамики, нужно прежде всего решить вопрос о том, для какой системы отсчета эти законы и, в частности, закон инерции применимы вообще.

Система отсчета, по отношению к которой выполняется закон инерции, называется основной или инерциальной системой, а движение, наблюдаемое по отношению к этой системе, называется абсолютным. Любая система отсчета, совершающая относительно инерциальной системы поступательное, прямолинейное и равномерное движение, будет также инерциальной системой. Всякая же система отсчета, движущаяся относительно инерциальной непрямолинейно или хотя бы и прямолинейно, но неравномерно, уже не будет инерциальной системой.

В подавляющем большинстве задан динамики, с которыми приходится иметь дело в обычной технической практике, можно с вполне достаточной точностью считать инерциальной систему отсчета, неподвижную относительно Земли. Поправки приходится при этом вводить лишь в тех сравнительно редких случаях, когда вращением Земли пренебрегать нельзя: в задачах артиллерии и ракет дальнего действия, при изучении морских и воздушных течений и некоторых других, очень быстрых или длящихся очень долго, движений.

Второй закон (основной закон динамики): ускорение, сообщаемое материальной точке приложенной к ней силой, пропорционально модулю этой силы и совпадает с ней по направлению.

Необходимо иметь в виду, что формулировкой закона предполагается, что точка, к которой приложена данная сила, совершенно свободна, т. е. не встречает никаких препятствий своему движению.

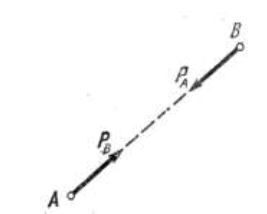
Рис. 1

Требуется подчеркнуть, что с направлением силы всегда совпадает направление ускорения, а не направление самого движения (направление скорости). Направление движения может и не совпадать с направлением приложенной к точке силы. Так, точка, брошенная в пустоте под углом к горизонту, движется при полете по кривой линии (параболе), все время изменяя направление своего движения, тогда как действующая на точку сила тяжести (и сообщаемое ею ускорение) всегда направлена по вертикали вниз.

Направление движения будет совпадать с направлением силы лишь в том случае, если она действует на свободную точку, находившуюся первоначально в покое. Если же точка уже находилась в движении, то сообщаемое данной силой ускорение лишь изменяет ее скорость, направление же скорости может при этом и не совпадать с направлением силы.

Третий закон (закон равенства действия и противодействия): силы, с которыми действуют друг на друга две материальные точки, всегда равны по модулю и направлены по одной прямой (соединяющей данные точки) в противоположные стороны.

Если материальная точка А действует на материальную точку В с силой РА, то точка В действует на точку А с силой РB = - РА (рис. 1).

Четвертый закон (закон независимости действия сил): ускорение, получаемое материальной точкой при одновременном действии на нее нескольких сил, равно геометрической сумме тех ускорений, которые

получила бы эта точка под действием каждой из данных сил в отдельности.

Пусть на точку, масса которой равна m, одновременно действуют силы P1, Р2, Р3, ..., Рn, сообщая ей при этом ускорение а. Ускорения, которые получила бы эта точка при раздельном действии на нее каждой из данных сил, обозначим через а1 а2, а3,... аn. Согласно данному закону, установленному на основании многочисленных опытов Галилеем, будем иметь a + a1 + a2 + a3 +…+ an

Если мы умножим обе части данного равенства на скалярный множитель m (на массу точки), то получим ma + ma1 + ma2 + ma3 +…+ man.

Согласно основному уравнению динамики ma1 = P1 ma2 = P2, та3 = Р3, ..., тап = Рn. Отсюда получаем ma = P1 + P2 + P3 +…+ Pn.Обозначив через Р равнодействующую системы сил, приложенных к данной точке, равную их геометрической сумме, будем иметь та = Р.

Следовательно, основное уравнение динамики остается в силе и в том случае, когда на точку одновременно действует несколько сил. Под приложенной к точке силой Р нужно понимать в этом случае равнодействующую всех сил, действующих на точку.

2. Теорема об изменении кинетической энергии механической системы

Кинетической энергией системы называется сумма кинетических энергий всех материальных точек системы.

Обозначая кинетическую энергию системы через Т, будем иметь

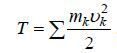. (1)

Таким образом, чтобы найти кинетическую энергию системы в какой-либо момент, надо массу каждой точки системы умножить на половину квадрата ее скорости и полученные произведения сложить.

Для материальной точки теорема об изменении ее кинетической энергии формулируется следующим образом: изменение кинетической энергии материальной точки на некотором пути равно работе приложенной к ней силы на том же пути.

Применим эту теорему к системе таких точек. Для одной материальной точки имеем равенство:

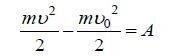
где 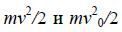 - значения кинетической энергии точки соответственно в конце и начале пути точки, А - работа силы, приложенной к точке на том же пути.

Написав подобные равенства для всех точек системы и сложив их почленно, мы, очевидно, получим

.

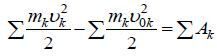Обозначая кинетическую энергию системы 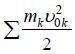 в ее начальном положении через То и кинетическую энергию системы  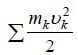в ее конечном положении через Т, окончательно получим

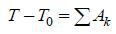. (2)

Изменение кинетической энергии при перемещении системы из одного положения в другое равно сумме работ всех сил (как внешних, так и внутренних), действовавших на систему при ее перемещении.

При вычислении суммы работ всех сил, действовавших на систему при ее перемещении, необходимо иметь в виду следующие обстоятельства, чрезвычайно упрощающие практическое применение теоремы об изменении кинетической энергии во многих случаях.

1. При всяком перемещении твердого тела (т. е. системы, расстояния между точками которой не изменяются) сумма работ его внутренних сил равна нулю.

2. Сумма работ реакций идеальных связей, неизменных во времени, при всяком перемещении системы, допускаемом этими связями, равна нулю.

Последнее обстоятельство автоматически исключает из уравнения кинетической энергии системы реакции идеальных связей. Если же связи не идеальные, т. е. трением в них пренебречь нельзя, то в сумму работ сил, приложенных к системе, нужно включить и работу сил трения.

При применении теоремы об изменении кинетической энергии системы очень часто приходится вычислять кинетическую энергию движущегося твердого тела. Найдем ее выражения при важнейших видах движения тела.

Тело движется поступательно. Если твердое тело движется поступательно, то скорости всех его точек в каждый момент равны между собой. Следовательно, в данном случае кинетическая энергия тела

.

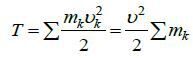Обозначая 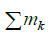 т. е. сумму масс всех точек тела, через М, получаем

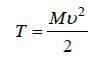. (3)

Кинетическая энергия Т поступательно движущегося твердого тела равна половине произведения массы М тела на квадрат его скорости υ.

Таким образом, кинетическая энергия поступательно движущегося тела, вычисляется совершенно одинаково с кинетической энергией материальной точки.

По формуле (3) вычисляется также и кинетическая энергия любой системы), движущейся так, что модули скоростей всех ее точек одинаковы.

Тело вращается вокруг неподвижной оси. Модуль υk скорости любой k-й точки твердого тела, вращающегося вокруг неподвижной оси, равен, как известно, произведению угловой скорости ω тела на расстояние rk данной точки от оси вращения тела: .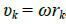

Следовательно, кинетическая энергия вращающегося тела

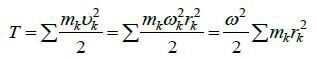
Но  т.е. сумма, составленная из произведений масс точек тела на квадраты их расстояний до оси вращения тела, есть не что иное, как момент инерции J тела относительно его оси вращения.

Следовательно, при данном движении тела

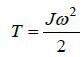. (4)

Кинетическая энергия Т тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции J тела относительно оси вращения на квадрат угловой скорости ω.

Сравнивая формулу (4) с формулой (3), можно заметить, что строение их аналогично. В формуле (4) роль массы играет момент инерции тела, а роль линейной скорости - угловая скорость тела.

Тело совершает плоскопараллельное движение. Пусть тело совершает плоскопараллельное движение, т. е. все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости. Представим себе сечение тела (рис. 2) плоскостью, проходящей через центр тяжести С тела и параллельной данной неподвижной плоскости. Допустим, что нам известна угловая скорость ω фигуры и скорость υc ее центра тяжести.

Кинетическую энергию тела, совершающего плоскопараллельное движение, можно вычислить по формуле (4):

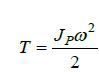, (5)

где Jp - момент инерции тела относительно его мгновенной оси вращения. Пользование этой формулой для нахождения кинетической энергии тела при его плоскопараллельном движении затрудняется тем, что требует для каждого момента времени определения положения мгновенной оси вращения тела и вычисления соответствующего ей момента инерции тела. Преобразуем поэтому формулу (5), воспользовавшись теоремой о моментах инерции относительно параллельных осей. Согласно этой теореме

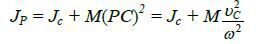 (6)

где Jс - момент инерции тела относительно оси, проходящей через центр масс тела и параллельной мгновенной оси, М - масса тела, PC = υc/ω -расстояние между рассматриваемыми параллельными осями.

Подставив выражение (6) момента инерции JP тела относительно мгновенной оси в формулу (5) кинетической энергии, найдем

.

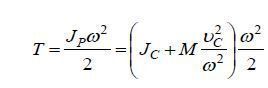Раскрыв скобки и произведя сокращение, окончательно получим

. (7)

Кинетическая энергия тела при его плоскопараллельном движении равна сумме тех кинетических энергий, которые имело бы данное тело при его поступательном движении со скоростью центра масс тела и при его вращательном движении вокруг оси, проходящей через центр масс тела и перпендикулярной к той неподвижной плоскости, параллельно которой движется тело.

Данную формулировку нетрудно запомнить, если принять во внимание установленное в кинематике положение о том, что всякое плоское движение может быть разложено на поступательное движение со скоростью полюса и вращательное движение вокруг полюса.

Только, в отличие от кинематики, выбор полюса здесь не произволен. При вычислении по формуле (7) кинетической энергии тела при его плоскопараллельном движении за полюс надо обязательно выбирать центр масс тела. Если за полюс принять другую точку тела, то мы получим иную, чем (7), формулу для его кинетической энергии.