Лекция Оценка возможных движений механизмов

« Назад

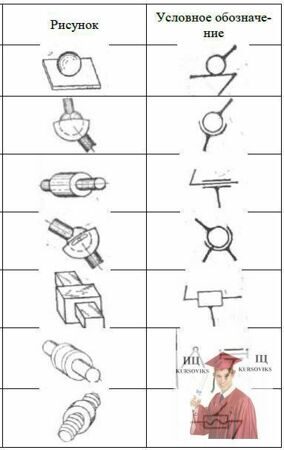
Таблица 1 - Условные обозначения кинематических пар

Класс пары	Число условий связи	Число степеней свободы	Название пары		Рисунок		Условное обозначение
I	1	4	Шар – плоскость
III	3	3	Сферическая
IV	4	2	Цилиндрическая
V	5	1	Сферическая с пальцем
V	5	1	Поступательная
IV	5	1	Вращательная
IV	5	2	Винтовая

Все пары делятся на пять классов, в зависимости от числа налагаемых связей на подвижность каждого из звеньев. Например, если телами (звеньями), образовавшими кинематическую пару, утрачено по 5 степеней свободы каждым, эту пару называют кинематической парой 5-го класса. Если утрачено 4 степени свободы – 4-го класса и т.д. Число степеней подвижности обозначается за 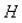. Число налагаемых связей обозначается за 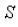. При этом число степеней подвижности можно определить по формуле: .

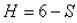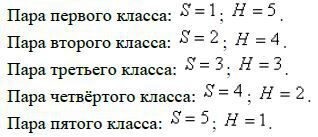
Рис. 1 – Кинематические пары различных классов

Рис. 2 – Примеры кинематических пар

1. Оценка возможных движений механизмов

Структурная модель кроме

1) демонстрации строения и принципа действия механизма

позволяет

2) сделать принципиальный вывод о том будут ли двигаться его звенья и движением, каких из них при этом следует управлять.

Необходимый результат получают из структурной формулы, которая вытекает из анализа структурной схемы механизма.

Структурными формулами называются закономерности, связывающие число степеней свободы Н кинематической цепи механизма с числом звеньев и числом и видом его кинематических пар.

Каждое звено, находясь в пространстве, имеет шесть степеней подвижности. Если таких звеньев k, то общее число степеней подвижности будет 6k.

Соединение звеньев в кинематические пары накладывает связи на относительное движение звеньев. Эти ограничения зависят от класса кинематической пары, т. е. числа условий связи.

Если число пар каждого класса обозначить через рn, где индекс n - номер ее класса, то в самом общем случае в кинематической цепи будет р1 пар первого класса, р2 пар второго класса и т.д. Следовательно, из 6k степеней подвижности, которыми обладают свободные звенья, следует исключить те степени подвижности, которые ограничиваются кинематическими парами. Тогда число степеней подвижности пространственной кинематической цепи будет

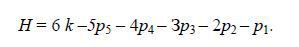 (1)

Если одно из звеньев кинематической цепи будет неподвижным (стойка), то степень подвижности кинематической цепи W (число степеней подвижности относительно звена, принятого за неподвижное) будет

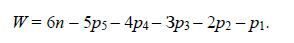 (2)

Если звенья механизма движутся в одной плоскости, то механизм называется плоским и структурная формула (2) для общего вида таких механизмов принимает вид

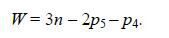 (3).

Эта формула впервые была предложена П. Л. Чебышевым в 1869 г.

Если W =1, то это значит, что достаточно задать движение только одного звена механизма (например, соединив его с двигателем) чтобы движение остальных звеньев было строго определено.

Если W = 3 то необходимо управлять движением трех его звеньев и т.д.

Если W = 0 то данная схема не является механизмом, т.к. передача движения с ее помощью невозможна.

Структурные формулы (2) и (3) получены из предположения, что все уравнения связи независимы.

В некоторых механизмах это условие не выполняется.

В общее число наложенных связей может войти q избыточных (повторных) связей, которые не уменьшают подвижности механизма, обращая его в статически неопределимую систему. Тогда формулы (2) и (3) принимают вид

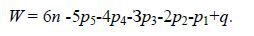 (4)

и

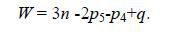 (5)

Из формул (4) и (5) получаем

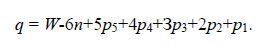 (6)

и

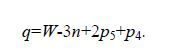 (7)

При q = 0 механизм представляет собой статически определимую систему, и сборка его происходит без деформации звеньев (самоустанавливающийся механизм), а при q>0 - статически неопределимую систему. Сборка и движение такого механизма происходят при деформации его звеньев.

В уравнении (6) неизвестны W и q и решение его представляет большую сложность.

В реальном механизме между элементами кинематических пар имеются зазоры, а при движении механизма его звенья могут деформироваться. Это является источником шума.

При проектировании механизмов следует выполнять два основных требования.

Во-первых, точность изготовления деталей и монтажа опорных и корпусных деталей должна быть определена из условия отсутствия защемления элементов кинематических пар.

Во-вторых, жесткость корпусных деталей должна быть достаточно высокой, чтобы исключить возможность перекоса осей вращения кинематических пар и параллельного смещения осей шарниров или направляющих, обусловленных деформацией корпуса.

В противном случае появляется возможность защемления элементов кинематических пар и усиленного изнашивания пар трения.

Все механизмы, в том числе и плоские, при анализе и синтезе структуры должны рассматриваться как пространственные.

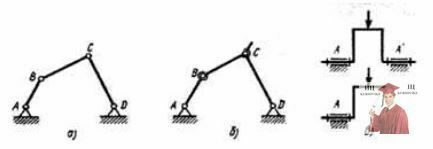
Рис. 3 - Схемы к определению избыточных связей

а - четырехзвенный механизм с парами пятого класса; б - четырехзвенный механизм с парами третьего, четвертого и пятого классов; в - сложные кинематические пары (одно - и двухопорный коленчатый вал)

В плоском четырехзвенном механизме (рис. 3, а) все кинематические пары пятого класса являются одноподвижными. Если оси шарниров А, В, С, D строго параллельны между собой, то по формуле (3) степень подвижности W = 3n - 2р5 = 3∙3 - 2∙4 = 1. Если тот же механизм рассматривать пространственным, то при W=1 число избыточных связей [по (5)] будет: q = W – 6n + 5р5=1 – 6∙3 + 5∙4=3, т. е. в механизме имеются три избыточных связи. Устранение их достигается изменением подвижностей отдельных кинематических пар. Например, если шарнир В заменить сферической парой третьего класса, а шарнир С - сферической парой с пальцем (четвертый класс) (рис. 3, б), то избыточные связи в механизме будут отсутствовать и W=6n-5р5-4р4-Зр3+q = 6∙3-5∙2-4∙1-3∙1+0=1.

Устранение избыточных связей снижает требования к точности изготовления кинематических пар, способствует адаптации основания механизма к деформациям и погрешностям монтажа.

При проектировании машин часто применяются сложные кинематические пары. На рис. 3, в показаны схемы одноопорного и двухопорного коленчатых валов одноцилиндрового двигателя (при четырехцилиндровом двигателе может быть пять опор). С точки зрения кинематики вполне достаточна одноподвижная вращательная пара А. Для повышения жесткости такой системы ставят две опоры А и А'.

При анализе структуры системы вал - корпус машины эти две опоры считают как одну кинематическую пару. Эта пара будет сложной. При ее образовании могут быть внесены избыточные связи, которые здесь называются локальными или пассивными. Эти связи, позволяющие реализовать требуемое относительное движение звеньев, не сказываются на общих структурных свойствах механизма и должны рассматриваться независимо. Чтобы локальные связи не обратились в действующие, необходимо соблюсти требования точности изготовления и жесткости звеньев во избежание защемления пары.

В ряде случаев избыточные связи вводят специально для повышения жесткости механизма или устранения неопределенности движения звеньев механизма в некоторых его положениях.

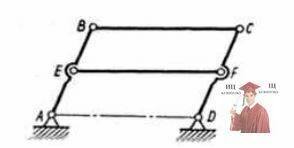
Рис. 4 - Механизм сдвоенного параллелограмма

Примером этому может служить механизм сдвоенного параллелограмма (рис. 4). Для получения значения W=1 необходимо строгое соблюдение геометрических соотношений АВ=СD, ВС=AD и ЕF=АD, если АЕ=DF, и высокой точности изготовления механизма. При этих условиях введение дополнительного звена ЕF не вносит новых геометрических связей. По формуле (3) степень подвижности механизма W=0, а фактически W=1. Звено ЕF введено для увеличения жесткости механизма и не дает возможности во время его работы из механизма параллелограмма получить механизм антипараллелограмма.

В ряде случаев в механизм вводят лишние степени подвижности. Примером может служить установка в соединение между двумя звеньями шариковых и роликовых подшипников, введение ролика между толкателем и кулачком и т. д. Их вводят в конструкцию механизма для того, чтобы уменьшить износ в кинематических парах.

2. Структурные группы Ассура

Под структурным анализом механизма понимается определение количества звеньев и кинематических пар, классификация кинематических пар, определение степени подвижности механизма, а также установление класса механизма по группам Ассура.

Группа Ассура названа по имени А. В. Ассура, который впервые фундаментально исследовал структурную классификацию плоских стержневых механизмов.

Группой Ассура называется кинематическая цепь, которая в случае ее присоединения элементами внешних пар к стойке получает нулевую степень подвижности, т. е. образует ферму.