Лабораторна робота №13, Задачі стохастичного програмування

« Назад

Теоретична довідка

Завдання для самостійної роботи

1. Повторити теоретичний матеріал лекції “Нелінійне програмування”.

2. Розглянути приклади розв’язування задач нелінійного програмування та дослідження їх оптимальності.

3. Виконати завдання лабораторної роботи.

4. Провести тестування програми на декількох прикладах та завданнях.

5. Зробити висновок, оформити результат виконання.

Теоретична довідка

Крім задач лінійного програмування існує цілий клас задач, залежність між змінними цільової функції яких не можна визначити лінійними рівняннями, крім того, системи обмежень також можуть (і, як правило, так воно і є) визначатися рівняннями та нерівностями, змінні в яких мають степені вищі за одиницю. Розглянемо задачу нелінійного програмування, коли на змінні цільової функції не накладено жодних обмежень. Таку задачу називають задачею без обмежень.

Коли в деякій точці значення є оптимальним, то воно буде оптимальним і по будь якій її змінній, а для них в цій точці похідна дорівнює нулю. Отже, необхідною умовою оптимальності точки х0 є

gradz(x0)=0.

Швидкість зростання функції в такій точці дорівнює нулю і її можна назвати точкою спокою.

Наведемо алгоритм знаходження максимуму цільової функції задачі НЛП без обмежень.

1. Знаходимо критичні точки, тобто ті в яких частинні похідні 1-го порядку рівні нулеві або не існують.

2. Визначаємо величини:

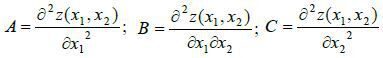
3. Складаємо детермінант .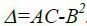

4. Якщо 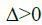, то функція має в М0 – екстремум. А саме: якщо А>0 (чи С>0) – мінімум; якщо А<0 (чи C>0) – мінімум; якщо А<0 (чи C<0) – максимум.

Якщо 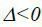, то в точці М0 екстремуму немає.

Якщо 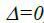, то проблема потребує додаткових досліджень.

Пакет електронних таблиць Excel дозволяє розв’язувати задачі нелінійного програмування за допомогою вже добре відомої нам програми „Поиск решения”. Наведемо приклад типової задачі нелінійного програмування з конкретним економічним змістом.

Задача. Органолептична оцінка випечених виробів із дріжджового тіста Y залежить від режиму температури – X1 та швидкості циркуляції повітря у жарильній шафі – X2. Експериментальні дані для Y, X1, X2 наведено в таблиці:

Таблиця 1

Експериментальні дані в Excel

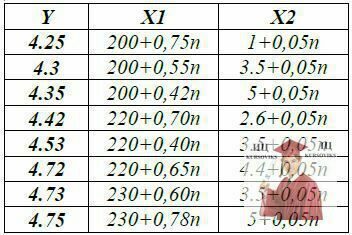
де n – порядковий номер студента в журналі.

На основі статистичних даних знайти регресійну залежність показника Y від змінних X1, X2.Визначити такий режим випічки виробів з тіста, при якому органолептична оцінка виробів буде максимальною.

Хід роботи

Приймемо гіпотезу про те, що між Y та X1, X2 існує стохастична залежність

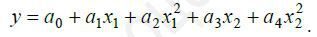
1. Для оцінки параметрів будуємо таблицю, вводячи блоки даних:

- для Y – A3:A10;

- для X1 – B3:B10;

- для X2 – D3:D10.

2. У блоках C3:C10 та E3:E10 формуємо квадрати відповідних значень X1 та X2.

3. Оцінки параметрів регресії та додаткову статистику формуємо у полі A12:E16:

- відзначимо блок, де будуть знаходитися розрахункові дані: ширина блоку рівна числу оцінюваних параметрів, а висота має п’ять рядків;

- вибираємо функцію Линейн та вводимо поступово вводимо вхідні дані і параметри.

- для того, щоб побачити у блоці всі розрахункові дані натискаємо F2, а потім Ctrl+Shift+Enter.

4. Оптимальний режим визначаємо з використанням “Поиск решения”:

- у комірки змінних вводимо початкові значення (мінімальні значення);

- у цільову комірку вводимо формулу функції, для якої потрібно знайти максимальне значення. У формулі замість X1, X2, а0, а1, а2, а3, а4 вказуємо адреси відповідних комірок;

- використовуючи Поиск решения знаходимо значення х1, х2.

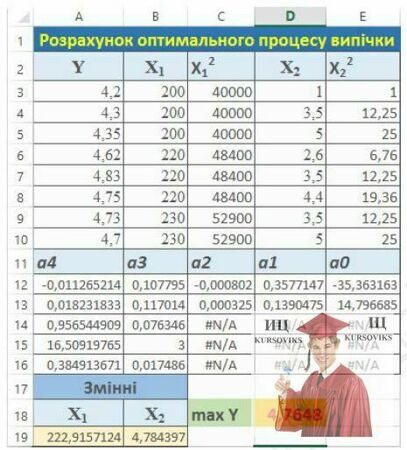
5. Отриманий результат має вигляд таблиці, наведеної нижче.

Рис. 1 – Розрахунок оптимального процесу випічки в Excel

Контрольні запитання

1. Сформулюйте загальну задачу нелінійного програмування. Які її особливості?

2. Що таке задача без обмежень?

3. Що називається частинною похідною, градієнтом, частинною похідною другого порядку?

4. Що таке точка спокою?

5. Наведіть алгоритм знаходження екстремуму цільової функції задач нелінійного програмування без обмежень.

6. Яке призначення статистичної функції Линейн? Яким чином організувати вхідні дані для її використання?

7. Як визначити оптимальне значення цільової функції з використанням програми Поиск решения?

8. Охарактеризуйте можливості діалогового вікна Поиск решения?

9. Яким чином потрібно змінити опції вікна для відшукання лінійної регресії? Мінімального значення функції?

10. Як накласти обмеження на початкові значенні параметрів?

11. Які вихідні дані функції Линейн?