Лабораторна робота №12, Нелінійне програмування, Оптимальна дивідендна політика

« Назад

Теоретична довідка

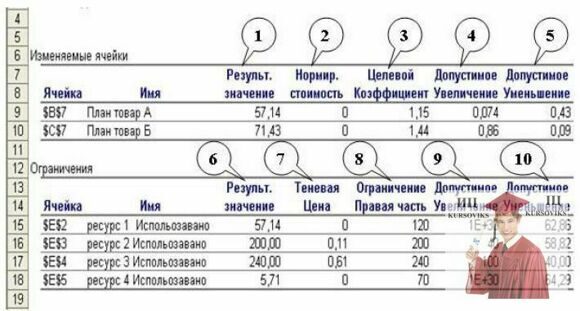
Рис. 1 – Звіт по стійкості в MS Excel

Звіт по стійкості (більш точним за змістом був би переклад з оригіналу sensitivity - чутливість) є найбільш цікавим і корисним - він визначає чутливість структури отриманого плану до змін початкових даних і, відповідно, подальші дії менеджера з метою поліпшення результатів. Такий звіт не створюється для моделей, значення в яких обмежені множиною цілих чисел. У разі нелінійних моделей звіт містить дані для градієнтів і множників Лагранжа.

1 - оптимальний план задачі. У нашому випадку, щоб отримати максимальну виручку в розмірі 168,37 гр. од ., Потрібно виробляти 57,14 одиниць товару А і 71,43 одиниць товару Б;

2 - нормована вартість стосується невідомих плану. Це невдалий переклад з оригіналу reduced cost, яку можна було перекласти, як «зменшена вартість. Цей показник, як зміниться оптимальне значення ЦФ при випуску продукції, якої немає в оптимальному плані. Наприклад, якщо нормована вартість товару А була б -3 (хоча в нашому випадку це 0), то примусовий випуск 2 одиниць товару А, яких немає в оптимальному плані призвів до зменшення Доходу на 2 • 3 = 6 і складав би 168,57 - 6 = 162, 57 д. од.

3 - коефіцієнти ЦФ;

4, 5 - межі змін значень коефіцієнтів ЦФ за умови, що кількість оптимальної продукції ( план) не зміниться. Наприклад, якщо цільовий коефіцієнт товару А (КА) дорівнює 1,15 (ціна за 1 одиницю товару), то змінюючи його в рамках 1,15-0,43 < КА < 1,15 +0,074 → 0,72 < КА < 1,224 план не зміниться, але значення доходу може зменшиться або збільшиться. Це можна перевірить якщо запустити програму «Пошук рішень», після внесень в таблицю змін даного коефіцієнта.

6 - кількість використаних ресурсів;

7. - тіньова ціна (в нелінійній моделі це множник Лагранжа) стосується обмежень, тобто, певне значення вказує на «цінність» обмеженого ресурсу в порівнянні з іншими ресурсами. Цей показник вказує як зміниться оптимальне значення ЦФ (Дохід) при зміні запасів ресурсів на 1 одиницю. Наприклад, якщо збільшити запас ресурсу 3 на 10 одиниць, то дохід збільшиться на 10 • 0,61 = 6,1 і становитиме 168,57 +6,1 = 174,67 д. од.

8 - запаси ресурсів;

9, 10 - задають діапазон для 8, в якому діє тіньова ціна 7 (аналогічно 4, 5). Наприклад, діапазон ресурсу 3: 200 < ресурс 3 < 340. Якщо ресурс 3 збільшити на 10 одиниць, то дохід збільшиться на 6,1 і становитиме 174,67. Якщо цей ресурс збільшити на 110 одиниць, то про дохід нічого сказати не можна, оскільки ми вийшли за вказані межі.

Хід роботи

Акціонерне товариство (АТ) ставить за мету, отримавши суму інвестицій, визначити таку дивідендну політику по тимчасових періодах (коли і скільки віддати), відповідно до якої за умови виконання зобов'язань перед акціонерами щодо виплат певної суми, максимізувати загальний дохід («віддати з розумом»).

Постановка: Маємо суму інвестицій у розмірі 100 гр. од., Потрібно визначити фінансову політику АТ протягом 4- х періодів, для кожного з періодів задана величина внутрішньої норми рентабельності, згідно з якою визначається прибуток в певний період.

Потрібно визначити суму дивідендів у кожному періоді за умови задоволення вимог щодо їх загальної суми таким чином, щоб загальний прибуток від інвестування був максимальний.

Економіко-математична модель

Знайти такий план дивідендної політики, щоб

Загальний прибуток = Сум. Вихід - Сум. Вхід → мах

При обмеженні:

1. Сума дивідендів = Обмеження на дивіденди;

2. Верхня межа> = Дивіденди> = Нижня межа.

Рис. 2 – Розрахунок оптимальної дивідендної політики в Excel

Створюємо таблицю з початковими даними. У першу клітинку рядка Інвестиція вводимо значення початкової інвестиції, в наступні вводимо формули посилання на клітинку рядка Віддача попереднього періоду. Рядок Прибуток заповнюємо формулами: Інвестиція поточного періоду*(1 + ВНР/100).

Контрольні запитання

1. Як обчислюється внутрішня норма рентабельності?

2. Як обчислюється прибуток?

3. Який зміст зменшеної вартості?

4. Який зміст Т-ціни?

5. Який зміст дозволеного збільшення?

6. Який зміст дозволеного зменшення?

7. Що таке дивіденди?

8. Що таке інвестиція?