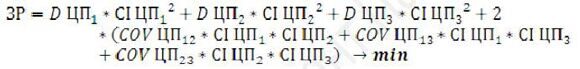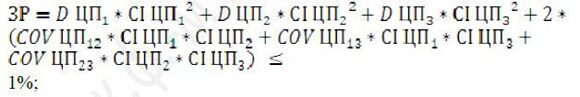Лабораторна робота №9, Оптимальний портфель інвестицій, Модель Шарпа

« Назад

Теоретична довідка

Це - типова, важлива і дуже поширена фінансова задача, яка з'являється в практиці ресурсного забезпечення, страхування, інвестування, банківської справи і тощо, де мова йде про пошук оптимального варіанту розподілу цілого (як правило, суми грошей) на окремі частини.

Постановка. Інвестор бажає вкласти певну суму грошей у певну кількість цінних паперів (ЦП) і хоче визначити, яку частину цієї суми найкраще вкласти у кожен вид ЦП. Обраний набір ЦП носить назву інвестиційний портфель.

Кращим може бути один з двох альтернативних варіантів :

- мінімізація ризику при обмеженні на дохід;

- максимізація доходу при обмеженні на ризик.

В інвестиційному менеджменті набір частин суми інвестування називається портфель, оптимальний портфелем є такий набір, який інвестор визначає для себе кращим згідно відношенню між прибутковістю вкладень і ризиком втрати.

Дохід, отриманий за певний період часу від інвестування певної суми, яка виросла за цей період до деякої величини, тобто числом (позитивним чи негативним), яке обчислюється за такою формулою :

Дохід = (Сума отримана за період – Інвестована сума) / Інвестована сума.

Ризик в теорії інвестування прийнято вимірювати величиною можливого розкиду доходу портфеля від середнього значення, цей розкид в статистиці називають варіацією або дисперсією. Він обчислюється за формулою:

Ризик = СУММ (Дисперсія ЦП_M * Сума інвестиції ЦП_M^2) + 2*СУММ (Коваріація ЦП_ML * Сума інвестиції ЦП_M * Сума інвестиції ЦП_L)

Початкові дані для цього завдання міститися в таблиці статистики доходів для всіх ЦП, зібраної за певну кількість періодів. З цією таблиці можна отримати:

- середнє значення доходу від визначеного ЦП: = СРЗНАЧ(Діапазон);

- варіацію (дисперсію) доходу від визначеного ЦП: = ДИСПР(Діапазон);

- коваріацію (число, яке характеризує залежність доходу від двох ЦП, які певним способом пов'язані між собою і впливають один на одного) доходу від визначеного ЦП: = КОВАР(Діапазон 1; Діапазон 2).

Існує два варіанти цієї задачі:

1. значення середніх доходів, їх варіацій і коваріацій задані (модель Марковіца);

2. задана статистика доходів, з якої знаходять значення середніх доходів, їх варіацій і коваріацій (модель Шарпа).

Хід роботи

Нижче розглянуті два завдання моделі Шарпа (на мінімум і максимум).

Задача 1. Мінімальний ризик

Інвестування стосується трьох цінних паперів, для яких відомо тільки прибутковість за 12 місяців, а дисперсію і коваріацію, які є оцінками ризику, потрібно знайти з даної статистики прибутковості ЦП і далі визначити значення оптимального портфеля, яке забезпечить мінімальний ризик. При чому, зафіксоване обмеження на величину доходу (5%) і на величину першого ЦП (не більше як (50-n)% від загальної суми).

n – порядковий номер студента в журналі

1. Знайти план інвестування (портфель) такий, щоб

2. Загальний ризик

де D – дисперсія;

ЗР – загальний ризик;

COV – коваріація;

СІ – сума інвестицій.

3. При обмеженнях:

a. Сума частин портфеля = 100%;

b. Сума доходу = 5%;

c. Вкладення в ЦП 1 <= (50-n)%, всі невідомі більше нуля.

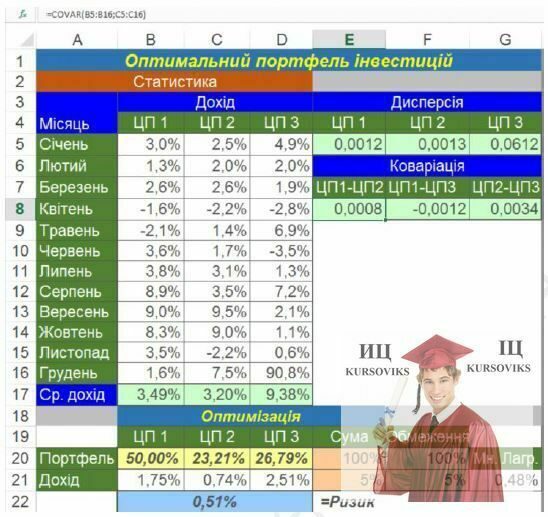
Рис. 1 – Оптимальний портфель інвестицій, Excel

4. Множник Лагранжа отримуємо із «Анализа по устойчивости».

Задача 2. Максимальний дохід

Інвестування стосується трьох ЦП, для яких відомо тільки прибутковість за 12 місяців, а дисперсію і коваріацію, які є оцінками ризику, потрібно знайти з даної статистики прибутковості ЦП та визначити значення оптимального портфеля, яке забезпечить максимальний дохід. При чому, зафіксоване обмеження на величину ризику (1%) і на величину ЦП (не більше як 0,4 загальної суми).

Рис. 2 – Проведення оптимізації, коваріації портфелю інвестицій, Excel

1. Знайти план інвестування (портфель) такий, щоб

2. Загальний дохід = Середній дохід * Сума інвестування = мах

3. При обмеженнях: Сума частин портфеля = 100%;

a. Загальний ризик

b. Вкладення в ЦП <= 40%,

c. Всі невідомі більше нуля.

Контрольні запитання

1. Який зміст коефіцієнта Лагранжа?

2. Що таке дисперсія?

3. Що таке коваріація?

4. Як обчислюється ризик інвестицій?

5. Які два варіанти даної задачі вам відомі?