Лабораторна робота №5-6, Оптимізаційні моделі еволюційного програмування в Excel, розв'язання задачі комівояжера з обмеженнями alldifferent

« Назад

Теоретична довідка

Переважну більшість практичних задач оптимізації відносять до «важких» для комп'ютерної реалізації задач з-за явної нелінійності цільової функції й обмежень і необхідності врахування спеціальних граничних значень для шуканих невідомих. Тож вимушений й тому найбільш популярний шлях до пошуку глобального оптимуму — зведення цих задач до класичних моделей лінійного, цілочислового або хоча б опуклого програмування, зрозуміло, із втратою певних характерних властивостей об'єкта дослідження.

Однією з таких «важких» задач, яка має безліч застосувань, зокрема, як тест (benchmark) для дослідження нових алгоритмів, є класична задача про комівояжера (який має відвідати n міст з мінімальною довжиною контуру обходу), де кінцевий результат критично й експоненційно залежить від розміру задачі (значення n) – кількість можливих контурів обходу складає фантастичну величину n!

За узгодженням з компанією Microsoft до середовищ Excel 2007/2010 вбудовано вдосконалену надбудову Premium Solver, де для гладкої нелінійної оптимізації застосовується потужний метод узагальненого приведеного градієнта (Generalized Reduced Gradient, GRG).

У прикладній математиці «важкі» задачі оптимізації відносять до класу нелінійних задач із негладкою цільовою функцією й обмеженнями на невідомі різного типу, для яких безсилі класичні моделі й методи нелінійного програмування градієнтного типу щодо пошуку глобального оптимуму. Тож прогресивна й багато- обіцяюча надбудова Premium Solver має у своєму складі модуль негладкої нелінійної оптимізації під назвою Evolutionary Solver (у російськомовній версії Excel 2010 – Эволюционный поиск решения), що відповідає новітньому класу математичних моделей еволюційного програмування. В основі цього потужного, але мало ще відомого масовому користувачу модулю реалізація специфічного алгоритму направленого перебору під назвою «генетичний алгоритм» (ГА), де спільно застосовується генератор випадкових чисел й оригінальний обчислювальний механізм пошуку оптимуму, що відтворює еволюційні процеси живої природи. На відміну від стихійних методів спроб і помилок чи випадкового пошуку із накопиченням статистики, в ГА на кожному кроці-спробі здійснюється певне перекомбінування значень шуканих невідомих (мовою біології – мутація та схрещення) й розв'язується набір проміжних підзадач, щоб сформувати оновлений набір значень шуканих невідомих, який визначає краще за попереднє значення цільової функції. За цим алгоритмом можна знайти досить близький до оптимального розв'язок поставленої негладкої нелінійної задачі оптимізації солідного розміру.

Цей же модуль має ще одну цікаву й ефективну властивість, що детально розглядається у цій роботі, яка дозволяє застосувати для шуканих невідомих оригінальний вид обмежень під назвою alldifferent (в Excel 2010 — «все разные»).

Для задачі про комівояжера цей вид обмежень є надзвичайно корисним, бо приводить до суттєвого збільшення допустимого розміру задачі, що розв'язується в Excel, — замість задачі з n2 + n невідомими за цим обмеженням розв'язується задача лише з n невідомими. Скажімо, за допомогою методу

«гілок і границь» в Excel можна точно розв'язати задачу комівояжера за моделлю булевого програмування з n < 13, зате еволюційним методом з обмеженням «все разные» наближено, з відхиленням від оптимуму на 2-3 %, що для практики цілком прийнятно, розв'язується задача комівояжера з n < 2003 .

Появу надбудови Premium Solver слід вважати революційною подією у сфері прикладного оптимізаційного моделювання завдяки наявності доступних, потужних, ефективних й надзвичайно корисних засобів. На прикладі розв'язання класичної й «непідйомної» задачі комівояжера рядовий користувач (менеджер-аналітик, дослідник-практик, викладач, аспірант, студент і навіть учень старших класів) фактично вперше на звичайному ПК із встановленим процесором електронних таблиць Excel 2007/2010 отримав реальну можливість перейти від «іграшкових» задач про комівояжера з приблизно 10-12 містами для обходу й тривалістю пошуку до 15-20 хв. до розв'язання цієї ж задачі на порядок більших розмірів із такою ж тривалістю, яка зазвичай покриває реальні задачі, що виникають у практиці моделювання матеріальних чи фінансових потоків у мережах та в прикладній логістиці.

Задача комівояжера

Задача комівояжера (в теорії графів — задача пошуку найкоротшого гаміль- тонова контуру) дуже близька за своєю постановкою до типових потокових задач на графах: про найкоротший шлях, про призначення та про мінімальне покриття. Але ці задачі розв'язуються значно простіше, ніж задача комівояжера, тому й розв'язок задачі комівояжера базується на алгоритмах цих дещо простіших задач.

Уперше математична модель задачі про комівояжера (TSP, travelling salesmam problem) була визначена в 1930 р. (К. Менгер) у класі моделей комбінаторного програмування; для її комп'ютерної реалізації у 1950-ті роки (Дж. Данциг) була поставлена відповідна задача лінійного програмування4 (ЛП) із-за її схожості з транспортною задачею та задачею про призначення матричного типу. Правда, зразу ж виявилася непередбачувана проблема — при використанні лінійної моделі для задачі про призначення шуканий гамільтонів контур розривається на сукупність часткових підконтурів, що з'єднують певні групи точок. Ця постановка для повного графа з п вершинами містить п2 + п змінних і не менше половини цієї величини — це явні обмеження на невідомі, наступні неявні обмеження в процесі обчислень ставлять за мету ліквідацію часткових контурів. Тож хоча принципово симплекс-методом можна користуватися, але на практиці від нього відмовляються з-за його громіздкості й неефективності моделі ЛП. В Excel застосовується вбудований в «Поиск решения» точний симплекс-метод (див. нижче).

Наступний етап розробки алгоритмів для розв'язання задачі про комівояжера – більш продуктивний дискретний підхід з використанням розгалужень, алгоритмів направленого й скороченого перебору варіантів (адже повний перебір астрономічної п! кількості варіантів відпадає одразу) за допомогою дерева пошуку та моделі булевого програмування. У цьому напрямку розробляються точні й наближені методи і алгоритми пошуку оптимуму. В Excel для цього застосовується вбудований в «Поиск решения» точний метод «гілок і границь»5 (модель булевого програмування) і наближений еволюційний метод (модель еволюційного програмування).

Постановка задачі

Комівояжер (агент роздрібної торгівлі) має обійти п клієнтів (замовників, певних об'єктів, традиційно — міст) найкоротшим шляхом (якнайшвидше, з мінімальними витратами ресурсів) і повернутися у початковий пункт, побувавши у кожного клієнта лише раз. У ролі комівояжера може бути транспортний засіб з доставки товарів у заклади роздрібної торгівлі чи в певні пункти для поповнення запасів ресурсів (харчів, питної води, палива, ліків, джерел електроенергії) чи заміни персоналу, сміттєзбиральна техніка, кандидат в депутати, персонал контрольно-ревізійної служби, бригада обслуговування банкоматів, автобус з групою туристів тощо — усі вони мають на меті визначити оптимальний контур обходу відповідних об'єктів, щоб мінімізувати довжину, час чи інші витрати.

Аналогічну постановку має виробнича задача про переналагодження універсального обладнання для послідовного виконання на ньому n різних операцій із мінімальною загальною тривалістю усього процесу, задача про найкоротше з'єднання n електронних елементів на мікросхемі та багато інших.

Класична постановка задачі комівояжера доповнюється рядом специфічних чи узагальнених задач, коли, скажімо, комівояжер має відвідувати певні групи міст у межах певних регіонів чи коли треба визначити

«вузьке місце» в контурі обходу — ці умови ще додатково ускладнюють й без цього непросту задачу в класичній постановці, але ж досягнення оптимального чи хоча би близького до нього варіанта забезпечує явну економічну чи іншу ефективність.

Ця математична задача припускає просту наочну інтерпретацію, з чого й розпочинається її постановка: на площині задано n точок із відповідними координатами, де кожна точка з'єднана із усіма іншими n точками. Це — набір даних (V, D, А, X, S), де

V = {1, ..., n} — задана множина n вузлів (номери, назви, коди);

D ={(i, j)} — задана множина n2 дуг: (1, 1), (1, 2), ., (n, n), кожна (i, j)-та дуга (і≠j) графа з'єднує певну пару вузлів i, j є V, це — повний граф, для якого існує розв'язок; для неповного графа існування розв'язку не гарантується;

А = {аij} — задана множина вагових коефіцієнтів чи параметрів дуг, це: відстань, тривалість, витрати палива, коштів чи будь-яких ресурсів, для i = j, аij

= ∞; при aij = aji задача симетрична, інакше, у загальному випадку, несиметрична;

X ={xij} — шуканий результат у матричній формі, множина шуканих невідомих, де: xij = 1, якщо (і, j)-та дуга належить шуканому контуру, xij = 0 — в іншому випадку, або X = {хi} — шуканий результат у векторній формі, множина шуканих невідомих у вигляді комбінації n номерів вузлів;

S – схема контуру на площині.

Відповідно, для постановки та розв'язання задачі про комівояжера маємо зважений граф (або неорієнтовану мережу), де треба знайти найкоротший замкнений контур, який складається точно з n дуг і проходить через кожен вузол один лише раз (це задача про мінімальний гамільтонів контур, що визначена ірландським математиком Гамільтоном у 1800-ті роки, яка довгі роки сприймалася як звичайна головоломка).

Задача оптимізації

1. Знайти план 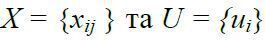, такі, щоб

2. 

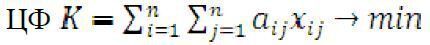
3. за обмежень:

а) 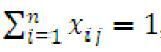, з кожного вузла можна вийти 1 раз;

б) 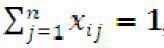, у кожен вузол можна увійти 1 раз;

ці два обмеження забезпечують умову 1-разового відвідування кожного міста;

в) 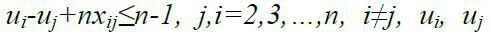 довільні значення, при 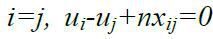; це обмеження забезпечує неможливість розриву контуру на окремі підконтури та граничних умов: усі .

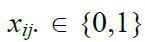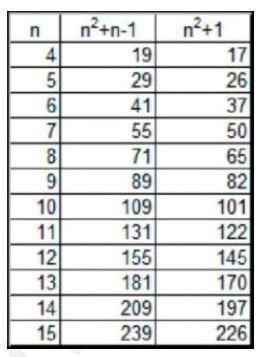
Таким чином, для задачі обходу n міст треба знайти: n2 значень матриці X, n-1 значень вектора U, разом: п2+ п - 1 невідомих із загальним числом обмежень n2 + 1 (див. табл.). Отже, з допустимим числом невідомих (200) і обмежень (100) в Excel можна розв'язати задачу комівояжера з числом міст до 13.

Хід роботи

Приклад 1. Симплекс-метод лінійного програмування

Постановка задачі

На площині задано координати 6 пунктів, розв'язати задачу комівояжера як закриту задачу про призначення (кількість претендентів = кількості вакансій). Математична модель:

1. Знайти план 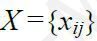такий, щоб

2. 

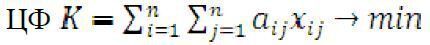
3. за обмежень:

а) 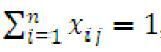, з кожного вузла можна вийти 1 раз;

б) 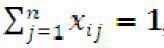, у кожен вузол можна увійти 1 раз;

ці два обмеження забезпечують умову 1-разового відвідування кожного міста та граничних умов: усі .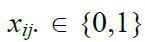

Порядок роботи

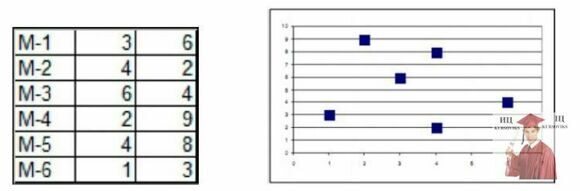
1. Увести назви міст і їхні координати.

2. Побудувати діаграму Точечная:

Рис. 1 – Діаграма Точечная в Excel

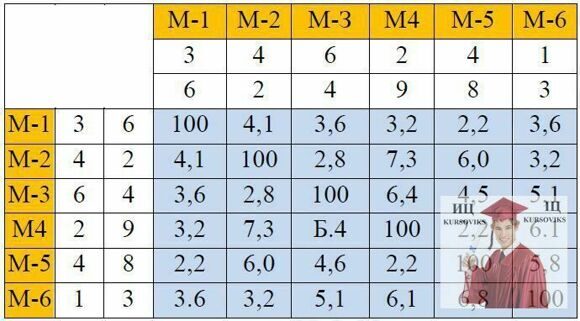
3. Сформувати матрицю відстаней A(6,6) обчисленнями значень aij за формулою: 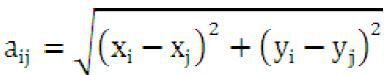усі діагональні елементи  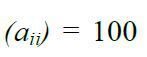(аналог ∞):

Таблицю початкових даних координат заповнюють випадковими числами.

Відстані обчислюються.

Розмірність таблиці повинна бути іншою.

(дана таблиця є ілюстративною)

Таблиця 1

Початкові дані координат

4. Сформувати матрицю Х, знайти суми елементів за рядками та стовпцями й обчислити значення цільової функції (ЦФ):

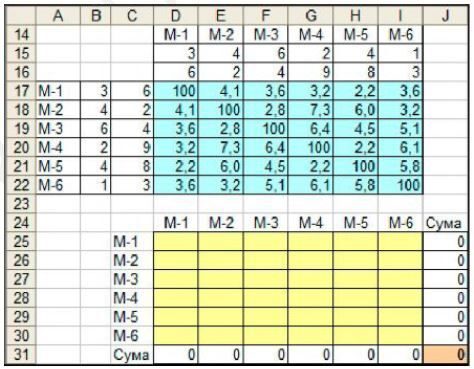
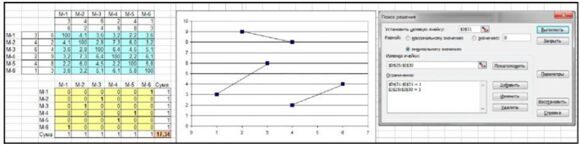
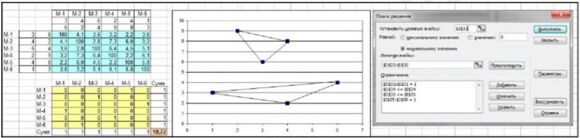
5. Сформувати табличну модель задачі про призначення й знайти її розв'язок. Як і передбачалося, шуканий контур розпався на три підконтури: (1- 6-1), (2-3-2), (4-5-4), які побудовано на діаграмі, значення плану: (х16, х23, х32, х45, х54, х61) = 1, інші – нулі, ЦФ = 17,34:

6. Вирішуємо розірвати підконтур (1-6-1), для цього формуємо додаткове обмеження: х16+ х61 < 1 й уводимо в модель; отримано новий результат, за яким є два підконтури: (1-3-2-6-1) та (4-5-4), значення ЦФ збільшилося на 0,33:

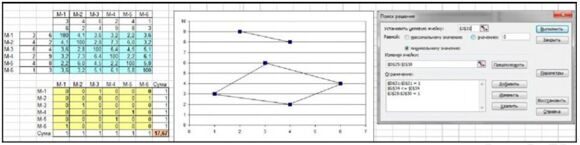
7. Вирішуємо розірвати підконтур (4-5-4), для цього формуємо друге додаткове обмеження: х45 + х54 < 1 і вводимо в модель; отримано новий результат, за яким є два підконтури: (1-5-4-1) та (2-3-6-2), значення ЦФ збільшилося на 1,05:

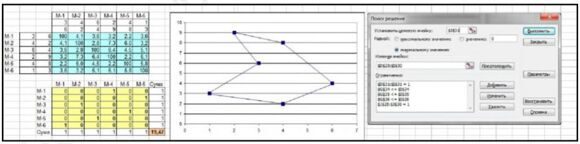
8. Вирішуємо розірвати підконтур (1-5-4-1), для цього формуємо третє додаткове обмеження: х15 + х51 + х54 + х45 + х41 + х14 < 2 і вводимо його в модель; отримано новий результат, за яким знайдено оптимальний контур (1- 4-5-3-2-6-1), його мінімальна довжина (значення ЦФ) дорівнює 19,47:

Висновок: модель лінійного програмування вимагає виконувати багато допоміжної роботи щодо визначення підконтурів для розірвання та уведення відповідних обмежень.

Приклад 2. Метод «гілок і границь» булевого програмування

Постановка задачі (див. Приклад 1). Використовується наведена вище математична модель. Порядок роботи.

Виконати пункти 1-5.

6. Сформувати допоміжну матрицю з метою реалізації обмеження (в), використавши шаблон матриці Х.

7. Визначити стовпець із 5 клітинок для елементів u. шуканого вектора U, транспонуванням ui визначити рядок з 5 клітинок для елементів uj.

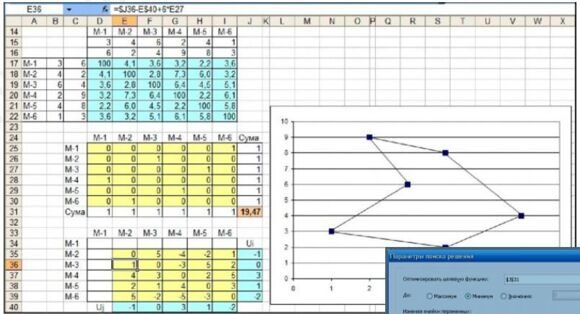
8. Сформувати матрицю лівих частин обмежень, на її діагоналі нулі:

Рис. 2 – Матриця лівих частин обмежень, по діагоналі нулі

9. У табличну модель увести обмеження (в), для цього у вікні Поиск решения:

- у поле Изменяя ячейки додати адреси елементів uj;

- у полі Ограничения: додати обмеження на двійковий тип матриці Х та обмеження (в);

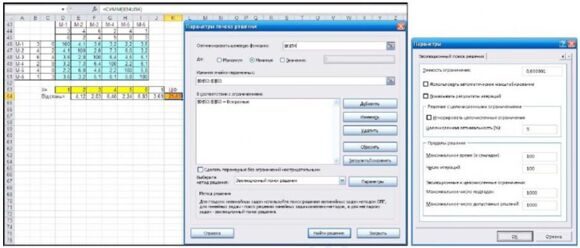
- у вікні Параметры поиска решения зняти галочку з позиції Неотрицательные значения, оскільки змінна u. може приймати довільні значення.

Рис. 3 – Вікно Параметры поиска решения

Результат:

Висновок: цим методом можна знайти зразу шуканий контур обходу, але за цю можливість ми «розплачуємося» додатковими обмеженнями, тож область роботи цього методу суттєво обмежується граничними значеннями кількості невідомих та обмежень Excel: до 200 змінних і до 100 обмежень.

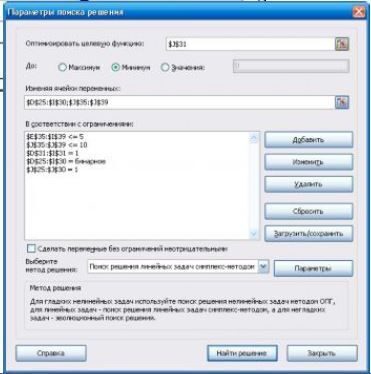
Зауваження. В середовищі Excel 2010 у вікно Параметры поиска решения треба внести такі зміни: для шуканих змінних Ui рекомендується внести певне обмеження, наприклад, не менше 10, далі у полі Выберите метод решения вибрати Поиск решения линейных задач симплекс-методом.

Приклад 3. Еволюційний метод

Цю ж задачу комівояжера для найкоротшого обходу 6 пунктів розв'яжемо за допомогою методу Эволюционный поиск решения в Excel 2010.

Позначення:

і — поточний номер шуканої змінної (співпадає із номером міста в контурі),

і = 1, ..., 6;

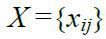– шуканий вектор невідомих, Х = {Х1, Х2, Хз, Х4, Х5, Хб};

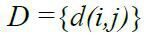– вектор відстаней між парами сусідніх вузлів у контурі обходу розміром з 6 елементів, де i<j (i передує j).

Задача оптимізації:

І. Знайти план обходу 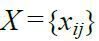, такий, щоб

ІІ. ЦФ: довжина контуру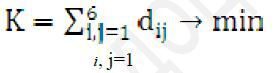 

ІІІ. За обмежень: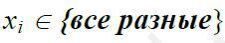 

Хід роботи

Повторити пункти 1-3.

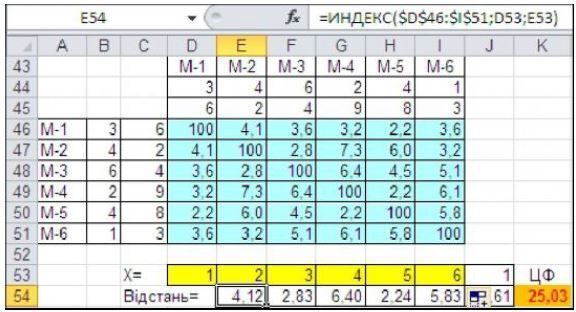
4. Сформувати рядок Х і заповнити його порядковими номерами, у наступній (n+1)-й клітинці зробити посилання на 1-й елемент цього рядка (щоб замкнути контур або цикл). Обчислити відстані між сусідніми клітинками за допомогою функції ИНДЕКС й обчислити їхню суму за допомогою функції СУММ.

5. Командою Данные → Поиск решения викликати вікно Параметры поиска решения і заповнити його поля вказаним чином.

6. Натиснути на Параметры, визначити у цьому вікні режим роботи програми, ОК і в попередньому вікні натиснути на Найти решение.

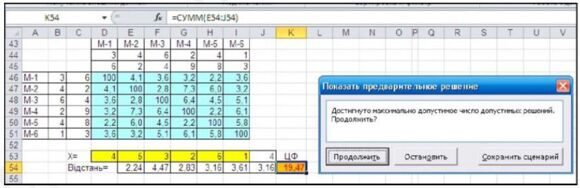
Починається процес обчислень – у рядку стану внизу вікна поступово виводиться повідомлення такого вигляду де видно: нове значення ЦФ, номер підзадачі і попереднє значення ЦФ.

Процес припиняється, коли значення ЦФ не змінюється в межах заданої точності або вичерпані граничні значення заданих параметрів і пропонується альтернатива: Продолжить/Остановить.

Процес оптимізаційного моделювання завершується за командою Остановить.

Результат.

Знайдено оптимальний контур обходу Х = {4, 5, 3, 2, 6, 1, 4} із мінімальною довжиною 19,47. Результат співпав з усіма попередніми результатами, але отримано його значно швидше з мінімальними витратами часу та розміру документа:

Початковими даними є координати географічних об'єктів чи тестові дані, що отримані за допомогою генератора випадкових чисел.

Контрольні запитання

1. В чому суть задачі комівояжера?

2. Які способи розв’язування задачі комівояжера вам відомі?

3. Які обмеження на кожен спосіб розв’язування?

4. Який розмір матриці допускається?

5. В чому перевага еволюційного методу розв’язування?