Лабораторна робота №8, Міжгалузеві балансові моделі в аналізі економічних показників

« Назад

Мета: отримати навички застосування моделі МГБ для аналізу економічних показників.

ХІД РОБОТИ

Уважно прочитати і розібратись добре у наведеному прикладі, скласти конспект. Ця тема і такі приклади будуть на екзамені.

Теоретичні відомості

Різноманітні модифікації моделі міжгалузевого балансу виробництва й розподілу продукції в народному господарстві дозволяють розширити коло показників, що їх охоплює модель. Розгляньмо застосування міжгалузевого балансового методу для аналізу таких важливих економічних показників, як праця, фонди, ціни.

Важливими аналітичними можливостями даного методу є, зокрема, визначення прямих і повних витрат праці на одиницю продукції та розроблення на підставі цього балансових продуктово-трудових моделей; вихідною моделлю тут слугує звітний міжпродуктовий баланс у натуральному вираженні.

Позначимо витрати живої праці для виробництва j-го продукту через L_j, а обсяг виробництва цього продукту (валовий випуск), як і раніше, через X_j, тоді прямі витрати праці на одиницю j-го виду продукції (коефіцієнта прямої трудомісткості) можна подати формулою:

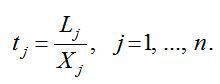 (1)

Уведемо таке поняття, як повні затрати праці — сума прямих затрат живої праці та затрат уречевленої праці, які переносяться на продукт через використані засоби виробництва. Якщо позначити величину повних затрат праці на одиницю продукції j-го виду через T_j, то добутки a_ij T_j відбивають затрати уречевленої праці, перенесеної на одиницю j-го продукту через і-й засіб виробництва. Припускається, що коефіцієнти прямих матеріальних витрат a_ij виражені в натуральних одиницях. Тоді повні трудові затрати на одиницю j-го виду продукції (коефіцієнти повної трудомісткості) дорівнюватимуть:

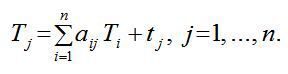 (2)

Уведемо до розгляду вектор-рядок коефіцієнтів прямої трудомісткості

 

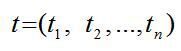
i вектор-рядок коефіцієнтів повної трудомісткості

 

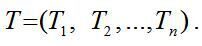
Тепер, із використанням розглядуваної вище матриці коефіцієнтів прямих матеріальних витрат А (у натуральному вираженні), систему рівнянь (1) можна подати в матричному вигляді:

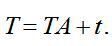 (3)

Виконавши відповідні математичні перетворення з використанням одиничної матриці Е, а власне:

 

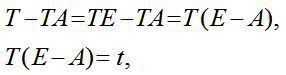
дістанемо таке співвідношення:

 

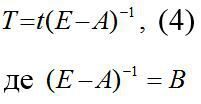
де

є матрицею коефіцієнтів повних матеріальних витрат, отже,

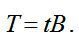 (5)

Позначимо через L величину сукупних затрат живої праці за всіма видами продукції, котрі з урахуванням (1) дорівнюватимуть

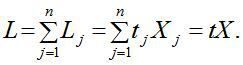 (6)

Використовуючи співвідношення (6) та (5), дістанемо:

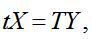 (7)

де t і Т — вектор-рядки коефіцієнтів прямої та повної трудомісткості, а Х та Y — вектор-стовпці валової та кінцевої продукції відповідно.

Рівняння (7) є основним балансовим рівнянням у теорії міжгалузевого балансу праці. Його конкретний економічний сенс полягає в тому, що вартість кінцевої продукції, яка оцінена за пов­ними затратами праці, дорівнює сукупним затратам живої праці. Порівнюючи споживчий ефект різних взаємозамінюваних продуктів з повними трудовими затратами на їх випуск, можна аналізувати порівняльну ефективність їх виробництва.

За допомогою показників повної трудомісткості більш повно й точно, ніж за використання існуючих вартісних показників, виявляється структура витрат на випуск різних видів продукції, а також співвідношення між затратами живої й матеріалізованої праці.

На підставі використання коефіцієнтів прямої та повної трудомісткості можуть розроблятися міжгалузеві й міжпродуктові баланси затрат праці та використання трудових ресурсів. Схематично ці баланси будуються за спільним типом матричних моделей, а всі показники в них (міжгалузеві зв’язки, кінцевий продукт, умовно чиста продукція тощо) виражаються в трудових вимірювачах.

ПРИКЛАД (виконати в Excel). Нехай у доповнення до вихідних даних попереднього прикладу, наведеного у підрозд. 4, задані також затрати живої праці (трудові ресурси) в розрізі трьох галузей: L₁ = 1160; L₂ = 460; L₃ = 875 — в однакових одиницях вимірювання. Треба визначити коефіцієнти прямої та повної трудомісткості й скласти міжгалузевий баланс затрат праці.

Розв’язання.

1. Скориставшись формулою (1) та розв’язком, отриманим при виконанні ПОПЕРЕДНЬОЇ лабораторної роботи:

 

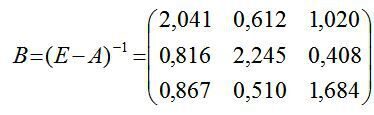
Міжгалузевий баланс виробництва й розподілу продукції

 

Знайдемо коефіцієнти прямої трудомісткості:

 

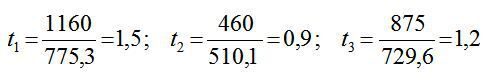
2. За формулою (23) знайдемо коефіцієнти повної трудо-місткості:

 

3. Перемножуючи відповідно перший, другий і третій рядки першого та другого квадрантів міжгалузевого матеріального балансу, побудованого в попередньому прикладі, на відповідні кое­фіцієнти прямої трудомісткості, отримаємо схему міжгалузевого балансу праці (в трудових вимірювачах) (табл. 3).

Таблиця 3

Міжгалузевий баланс затрат праці

Незначні розходження між даними таблиці та вихідними даними зумовлені похибками заокруглення в обчисленнях.

Розвиток основної (базової) моделі міжгалузевого балансу знайшов своє втілення також завдяки включенню в неї показників фондомісткості продукції. В найпростішому випадку модель доповнюється окремим рядком, в якому подані у вартісному вираженні обсяги виробничих фондів Ф_j, задіяних у кожній j-й галузі (j = 1, …, n). На підставі цих даних та обсягів валової продук­ції всіх галузей визначаються коефіцієнти прямої фондоміст­кості продукції j-ї галузі:

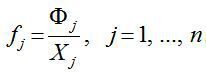 (26)

Коефіцієнт прямої фондомісткості показує обсяг виробничих фондів, безпосередньо задіяних у виробництві в даній галузі, в розрахунках на одиницю її валової продукції. На відміну від цього показника коефіцієнт повної фондомісткості F_j відображає обсяг фондів, необхідних у всіх галузях для випуску одиниці кінцевої продукції j-ї галузі (j = 1, …, n). Якщо a_ij — коефіцієнти прямих матеріальних витрат, то для коефіцієнтів повної фондомісткості справедливою буде рівність, аналогічна рівності (20) для коефіцієнтів повної трудомісткості:

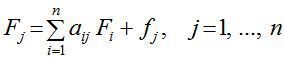 (27)

Якщо ввести до розгляду вектор-рядок коефіцієнтів прямої фондомісткості 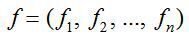 і вектор-рядок коефіцієнтів повної фондомісткості  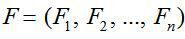то систему рівнянь (27) можна переписати в матричній формі:

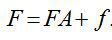  (28)

Звідси за допомогою перетворень, аналогічних використовуваним вище щодо коефіцієнтів трудомісткості, можна отримати матричне співвідношення

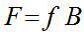, (29)

де B = (E – A) ^–1 — матриця коефіцієнтів повних матеріальних витрат.

Для глибшого аналізу потрібно деталізувати фонди на основні та обігові, а в межах основних — на будівлі, споруди, виробниче устаткування, транспортні засоби тощо.

Нехай у цілому всі виробничі фонди деталізовано на m груп. Тоді характеристика задіяних у народному господарстві фондів задається матрицею показників Ф_kj, що відображають обсяг фондів k-ї групи, задіяних у j-й галузі:

.

Коефіцієнти прямої фондомісткості також утворюють матрицю розмірності m ´ n, елементи котрої визначають обсяги виробничих фондів k-ї групи, безпосередньо використовуваних у виробництві одиниці продукції j-ї галузі:

 

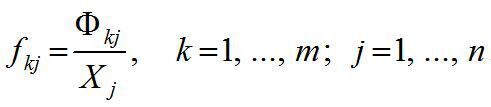
Для кожної j-ї галузі можна обчислити коефіцієнти повної фондомісткості F_kj, що відображають повну потребу в фондах k-ї групи для випуску одиниці кінцевої продукції цієї галузі:

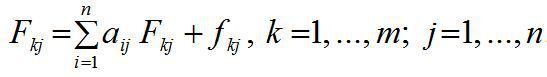 (30)

Розв’язок системи рівнянь (30) дозволяє подати коефіцієнти повної фондомісткості за кожною з груп фондів як функцію коефіцієнтів прямої фондомісткості:

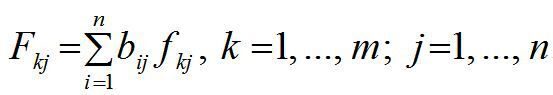 (31)

У формулах (30) та (31) величини a_ij та b_ij — це вже відомі коефіцієнти прямих і повних матеріальних витрат.

Коефіцієнти фондомісткості в міжгалузевому балансі дозволяють узгодити планований випуск продукції з наявними виробничими потужностями. Зокрема, потреба у функціонуючих фондах k-ї групи для отримання запланованого обсягу матеріального виробництва X_j, j = 1, …, n по всіх галузях задається формулою:

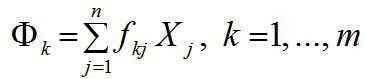 (32)