Лабораторна робота №6, Мережеві моделі

« Назад

Мета: навчитись будувати мережеві моделі економічних задач і застосовувати засоби MS Excel для їх розв’язання

ТЕОРЕТИЧНІ ВІДОМОСТІ

Транспортна модель і модель призначень є представниками більш загального класу моделей, що описують рух між початковими пунктами і пунктами призначення, які називаються мережевими моделями. Мережеві моделі часто застосовуються при рішенні організаційних питань і питань розподілу, а також в техніці і інформатиці. Багато реальних моделей зводяться до мережевих моделей. Як правило, за допомогою мережевого підходу описуються дуже масштабні ситуації.

Упродовж останніх десятирічь активно розробляється і впроваджується програмне забезпечення для систем поставок і планування матеріальних ресурсів, засноване на мережевих моделях. Основна увага в цих програмах звичайно надається стратегічному плануванню на стадіях поставок і розподілу. Терміни поставки і розподіл використовуються в достатньо загальному значенні: це можуть бути:

- потоки фізичної продукції;

- даних;

- транспортних засобів;

- валют різних країн і т. д.

В даний час рівень розвитку програмних мережевих додатків дозволяє оптимізувати моделі, що містять десятки тисяч змінних і обмежень (які дуже великі для засобу Пошук рішення).

Цілочисельні оптимальні рішення

Якщо модель можна представити у вигляді мережевої моделі, то, по-перше, теоретичні результати, встановлені для мережевих моделей загального вигляду, автоматично поширюються на її окремі випадки. Прикладом може служити властивість цілочисельності мережевої моделі.

 Якщо в моделі перевезення вантажів всі праві частини обмежень і пропускні спроможності дуг u_ij задаються цілими числами, то існує цілочисельне оптимальне рішення даної задачі.

В загальному випадку задача ЛП не гарантує існування цілочисельного оптимального рішення.

Для мережевої моделі з цілими значеннями правих частин і пропускних спроможностей дуг цілочисельне оптимальне рішення існує.

Ефективні процедури рішення

Друга перевага мережевих моделей полягає в тому, що структура такої моделі дає можливість застосовувати спеціальні методи рішення і програмне забезпечення, які дозволяють оптимізувати модель набагато швидше, ніж загальніший симплекс-метод, що використовується засобом Поиск решения. Завдяки цьому можна оптимізувати мережеві моделі великої розмірності швидше і дешевше. Результати застосування ефективних методів рішення, заснованих на спеціальній структурі мережевої моделі, просто вражаючі. Наприклад, компанія Internal Revenue Service створила мережеву модель, що містить 50 000 обмежень і 600 мільйонів змінних! Для оптимізації даної моделі потрібно тільки година роботи великої ЕОМ.

Далі розглянемо два різновиди задач, які виникають в мережевих моделях: задачі знаходження найкоротшого шляху і максимального потоку.

Зауваження. Кожну модель розмістити на окремому робочому аркуші книги Excel, який має ім’я - назву моделі.

 

ЗАВДАННЯ 1. Дослідити мережеву МОДЕЛЬ ПЕРЕВЕЗЕНЬ, реалізувати її у табличному процесорі MS Excel як модель ЛП і знайти розв’язок

Формулювання задачі

Андрій Ткаченко - начальник відділу збуту компанії ТМР, найбільшого дистриб'ютора продукції компанії AP, яка виробляє генератори. В даний час у розпорядженні Ткаченка є десять генераторів, які знаходяться в пункті, позначеному як пункт 1. Ці генератори необхідно доставити в пункти будівництва, позначені як пункт 3 і пункт 4. В пункті 3 потрібно три генератори, а в пункті 4 - сім. Через обмеження, що стосуються наявності водіїв, генератори можна доставляти тільки по маршрутах, показаних на рис.1 у вигляді графа.

- 1→2→3;

- 1→2→4→3;

- 1→2→5→4→3;

- 1→2→5→3.

 

Рис.1. Мережева діаграма (граф) для моделі Ткаченка

Ha рис.1 показаний приклад мережевої діаграми, або діаграми потоків. Кожна стрілка, що сполучає пункти, називається дугою або гілкою мережі. Дуга, що сполучає пункти 2 і 4, іноді символічно позначається парою чисел (2,4). Кожний пункт називається вузлом мережі.

Біля пункту 1 на рис.1 записано число +10. Це означає, що в даному пункті знаходиться десять генераторів (елементів поставки). Числа -3 і -7 поряд з пунктами 3 і 4 позначають потреби, або попит, в цих пунктах. З рисунка також випливає, що генератори можуть доставлятися в пункт 3 по будь-яких з можливих маршрутів:

- 1→2→3;

- 1→2→4→3;

- 1→2→5→4→3;

- 1→2→5→3.

Який з можливих маршрутів буде обраний, визначається витратами, пов'язаними з кожним маршрутом, і його пропускною спроможністю. Ці дані показані на рис. 2, де c_ij.- це питомі витрати (вартість перевезення одного генератора), а u_ij.- пропускна спроможність. Наприклад, витрати на переміщення одного генератора по дузі (5, 3) рівні с₅₃. Витрати складаються головним чином з вартості палива, мита, а також зарплати водія за середній час перебування в дорозі при русі по даному маршруту. Згідно укладеній раніше угоді з профспілкою компанія ТМР повинна міняти водіїв в кожному пункті маршруту. Через обмеження по наявності водіїв для кожної дуги існує верхня межа u_ij для кількості генераторів, яку можна по ній перевезти. Так, u₅₃ - верхня межа, або пропускна спроможність, дуги (5, 3).

 

Рис. 2. Мережева діаграма з даними про витрати і пропускнуздатністьмережі

Задача Ткаченко полягає в тому, щоб скласти такий план перевезень, який задовольнить попит з мінімальними витратами при дотриманні обмежень по пропускній спроможності.

Оцінимо різні варіанти перевезень. Наприклад, якщо (с₂₅ + с₅₃) менше, ніж с₂₃ , загальні витрати для шляху 1→2→5→3 будуть меншим, ніж для шляху 1→2→3, отже, шлях 1→2→5→3 вигідніший, ніж шлях 1→2→3. Проте максимальна кількість генераторів, яку можна відправити по вигіднішому шляху, рівна мінімуму від чисел u₁₂ , u₂₅ і u₅₃ . Якщо цей мінімум менше 3 (кількість генераторів, яку необхідно доставити в пункт 3), то не всі перевезення вдасться здійснити по маршруту 1→2→5→3. В нашій моделі тільки п'ять вузлів і вісім дуг, але навіть в такому простому прикладі оптимальне рішення не завжди очевидне.

Уявімо собі, що подібна модель складається з 300 або 400 вузлів і багато тисяч дуг, і стане зрозуміле, наскільки складними є задачі організації перевезень. Розглянута модель практично еквівалентна тій, що розглядалася раніше у транспортній моделі, але має дві особливості.

1. Будь-який завод або склад може здійснювати поставки будь-якому іншому заводу або складу.

2. Для кожного перевезення (гілки) можуть бути вказані верхні та/або нижні межі пропускної спроможності.

Дану модель Ткаченка легко сформулювати у вигляді моделі лінійного програмування. Нехай x_ij - загальна кількість генераторів, відправлених по дузі (i,j) - потік з вузла i в вузол j. Це змінні рішення.

Тоді модель прийме наступний вигляд:

Мінімізувати

 

при обмеженнях

 

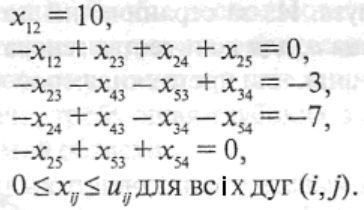
Дана модель має наступні властивості.

1. Це дійсно модель лінійного програмування. З кожною дугою мережі, зображеної на рис. 2, зв'язана одна змінна xij. Мережа містить вісім дуг, яким відповідає вісім змінних. Ціль - мінімізувати загальні витрати (сумарну вартість перевезень).

2. З кожним вузлом мережі пов'язане одне рівняння балансу потоків.

Перше рівняння показує, що загальний потік, що виходить з вузла 1, складає десять одиниць (що рівне загальному об'єму запасу у вузлі 1).

Друге рівняння показує, що загальний потік, що виходить з вузла, мінус загальний потік x₁₂, що входить у вузол 2, рівний нулю. Іншими словами, потік, що виходить з вузла 2, повинен бути рівний потоку, що входить у вузол 2. Третє рівняння показує, що для вузла 3 потік, що виходить, повинен бути на 3 одиниці менше, ніж той що входить. Це математичний спосіб виразити вимогу, щоб поставка у вузол 3 складала 3 одиниці. Аналогічно інтерпретуються рівняння для вузлів 4 і 5. Таким чином, рівняння для кожного вузла відображає умови матеріального балансу, беручи до уваги той факт, що вузол може бути точкою пропозиції, точкою попиту або ні тим, ні іншим. Проміжні вузли (такі як 2 і 5), які не є ні точками пропозиції, ні точками попиту, часто називаються вузлами перевалювання.

Нехай S_{вх -} сумарний потік, що входить у вузол j , S_вих - сумарний потік, що виходить з вузла j , S_{п –} пропозиція (попит) у вузлі j.

Тоді баланс потоків для вузла j задається формулою

S_вих -S_вх = S_п

3. Вузли з від’ємною пропозицією називаються пунктами призначення, стоками або точками попиту. Вузли з додатнім значенням пропозиції називаються джерелами або точками пропозиції. Вузли з нульовим значенням пропозиції називаються точками перевалювання. 3. Позитивні праві частини відповідають вузлам, які є постачальниками (джерелами). Негативні праві частини відповідають вузлам, що є споживачами (стоками). Нульові праві частини відповідають вузлам перевалювання, в яких не існує ні власного попиту, ні пропозиції. Сума значень правих частин всіх рівнянь рівна нулю, це означає, що сумарна пропозиція в мережі рівна сумарному попиту.

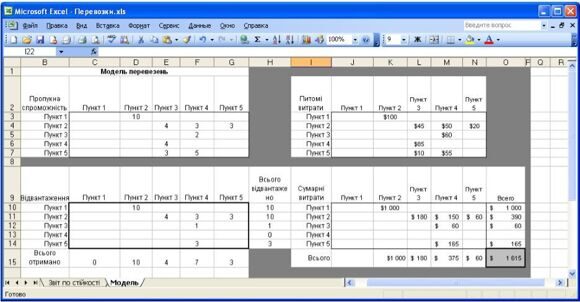
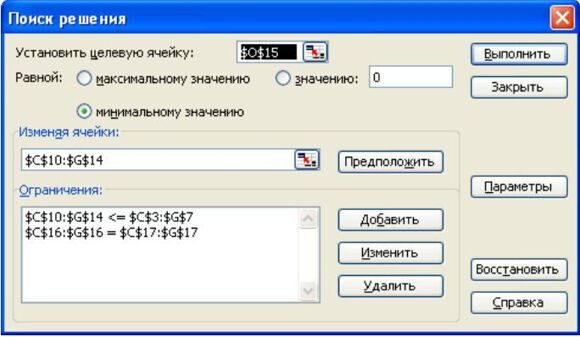
На рис. 3 показано табличне представлення даної моделі в Excel і відповідне оптимальне рішення. Матриця u_ij пропускних спроможностей дуг міститься в комірках C3:G7, а матриця c_ij питомих вартостей перевезень по дугах - в комірках J3:N7. Праві частини обмежень, задаючих значення попиту, введені в комірки C17:G17. Змінні рішення містяться в комірках C10:G14, а матриця сумарних витрат обчислюється по формулах в комірках J10:N14.

 

 

 

Рис. 3. Модель перевезення вантажів

ЗАВДАННЯ 2. Дослідити мережеву МОДЕЛЬ ПОШУКУ НАЙКОРОТШОГО ШЛЯХУ, реалізувати її у табличному процесорі MS Excel як модель ЛП і знайти розв’язок

Задача знаходження найкоротшого шляху виникає в мережі, в якій з кожною дугою (i,j) пов'язано число c_ij, що інтерпретується як відстань (або, можливо, вартість або час руху) від вузла i до вузла j. Маршрут, або шлях, між двома вузлами це довільна послідовність дуг, які сполучають дані вузли.

Задача полягає в знаходженні найкоротшого (що потребує мінімальних витрат або мінімального часу) шляху з певного вузла в решту вузлів мережі.

Ця задача природна для моделей перевезення продукції, пересилки пакетів даних по комп'ютерній мережі і т. д.

Як ілюстрацію, розглянемо наступну модель.

Формулювання задачі

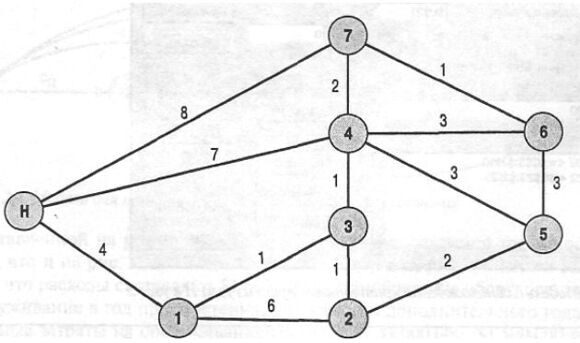
Бізнесмен Данило займається регулярними поставками вина в сім різних пунктів. На рис.4 показані ці пункти і сполучаючі їх маршрути. Зауважимо, що в даному випадку, на відміну від моделі перевезення вантажів, дуги ненаправлені. Таким чином, по кожній дузі допускається рух в обох напрямах. Можна, звичайно, зробити дуги направленими, при цьому вартість перевезення з вузла 1 у вузол 2 відрізнятиметься від вартості перевезення з вузла 2 у вузол 1. Така модель відповідає ситуації, при якій інтенсивність руху в одну сторону помітно вища, або ж з вузла 1 у вузол 2 рух можливий, а з 2 в 1 - ні (наприклад, вулиця з одностороннім рухом). Кожній дузі на рис.4 відповідає число, що позначає відстань між вузлами, що сполучаються даною дугою. Початковий пункт позначений Н. Данило вважає, що його сумарні витрати будуть мінімальні, якщо всі поставки в будь-який заданий пункт здійснюватимуться по найкоротшому маршруту. Тому його мета - відшукати найкоротші маршрути з вузла Н у всі решту сім вузлів.

 

Рис. 4. Мережа пунктів моделі Данила

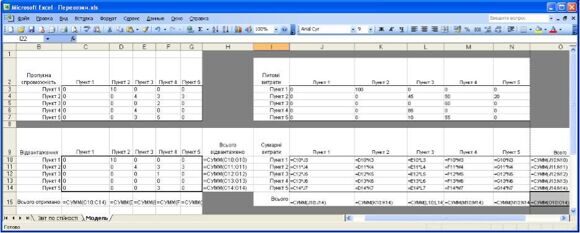
На рис.5 представлена модель Данила в Excel, оптимальне рішення - це найкоротші шляхи між двома будь-якими вузлами.

В даному випадку показаний оптимальний шлях з Н в пункт 5. На початковому вузлі Н і кінцевому вузлі 5 наголошено в рядку 22 числами 1 і -1 відповідно.

В діапазоні МЗ:Т10 вказані відстані уздовж різних дуг.

За винятком діапазону СЗ:J1О, де вказано, як вузли сполучені між собою за допомогою дуг, модель має той же вигляд, що і загальна модель перевезення вантажів, представлена на рис.2.

Змінні рішення повинні приймати значення 0 або 1, як і в моделі призначень, а цільова функція, яку необхідно мінімізувати, є сумарною відстанню.

 

 

 

 

Рис. 5. Модель знаходження найкоротшого шляху з пункту Н у пункт 5

ЗАВДАННЯ 3. Дослідити мережеву МОДЕЛЬ ЗАМІНИ ОБЛАДНАННЯ (УСТАТКУВАННЯ), реалізувати її у табличному процесорі MS Excel як модель ЛП і знайти розв’язок

Задачу знаходження найкоротшого шляху можна застосувати для оптимізації витрат на устаткування протягом певного часу.

Формулювання задачі

Менеджер Андрій Клівак відповідає в компанії, яка друкує періодичні видання, за покупку устаткування, зокрема, друкарських верстатів. Цього року йому належить вирішити, чи придбати новий дорогий друкарський верстат з низькими первинними витратами на обслуговування або продовжувати використовувати придбаний раніше друкарський верстат з високими витратами на обслуговування. Для простоти припустимо, що період планування в моделі Андрія Клівака складає чотири роки. Позначимо через c_ij витрати на придбання нового устаткування на початку року i (i = 1, 2, 3, 4) і обслуговування його до початку року j (j = 2, 3, 4, 5). Якщо устаткування може працювати тільки до початку року j де j < 5, то на початку року j необхідно знову купувати нове устаткування. Розглянемо три можливі варіанти поведінки.

1. Купувати нове устаткування на початку кожного року. Така політика приведе до найвищих витрат на придбання і мінімальних витрат на обслуговування. Загальні витрати на придбання і обслуговування у такому разі складуть c₁₂ + c₂₃ + c₃₄ + c₄₅.

2. Придбати нове устаткування тільки на початку першого року, а потім займатися його ремонтом і обслуговуванням протягом подальших років. При такій політиці сумарні витрати на придбання будуть мінімальні, а витрати на обслуговування максимальні. Загальні витрати на придбання і обслуговування складуть c₁₅.

3. Нове устаткування отримується на початку 1 і 4 років. Сумарні витрати складуть c₁₄ + c₄₅.

Зі всіх можливих варіантів Андрій хоче вибрати варіант з мінімальними сумарними витратами. Щоб вирішити цю задачу, необхідно знайти найкоротший шлях (в даному випадку - шлях з мінімальними витратами) з вузла 1 у вузол 5 для мережі, показаної на рис.6.

Кожний вузол на найкоротшому шляху означає заміну устаткування у відповідному році, тобто цього року необхідно придбати нове устаткування.

 

Рис. 6. Модель для ухвалення рішень по заміні обладнання (устаткування)

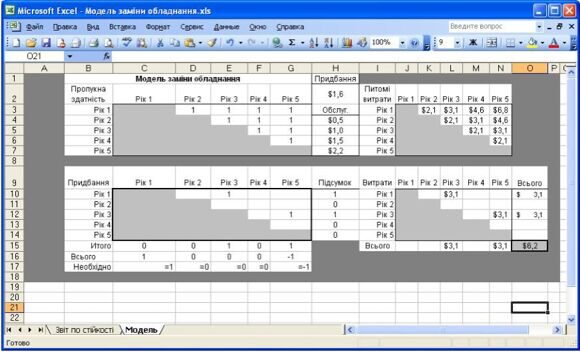
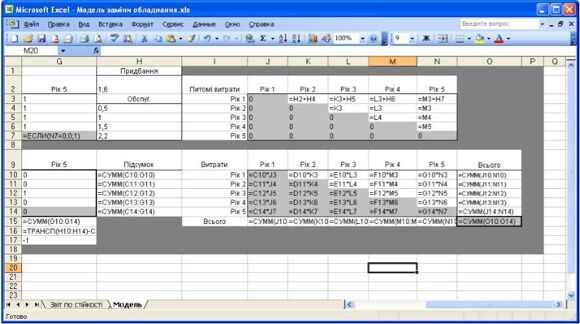
У представленій на рис. 7 табличній моделі використовується той же загальний макет і ті ж формули, що і на рис.2. Вартісні параметри задані в комірках Н2:Н7. Передбачається, що витрати складають 1 600 000 у.о. на придбання устаткування і 500 000 у.о. на його обслуговування в рік придбання; для кожного додаткового року експлуатації щорічні витрати на обслуговування складають1 000 000 у.о., 1 500 000 у.о. і 2 200 000 у.о. В комірках J3:N6 обчислені витрати на покупку і обслуговування друкарського верстата, якщо він придбаний в одному році і експлуатується до початку другого вказаного року. Комірки змінних рішення з сірим фоном в діапазоні C10:G14 відповідають неможливим рішенням із зворотним ходом подій (наприклад, придбання верстата в році 3 для використовування в році 1). На початковому і кінцевому роках використання устаткування наголошено в рядку 17 за допомогою чисел 1 і -1. В комірках C3:G7 міститься матриця зв'язків між вузлами, а в комірках J10:N14 обчислені витрати для вирішень, записаних в комірках C10:G14.

В даному випадку оптимальною стратегією є придбання нового друкарського верстата на початку років 1, використовування його протягом двох років і заміна на початку роки 3 новим друкарським верстатом, який потім використовується до початку років 5. При цьому загальні витрати за чотири роки складуть 6,2 млн. у.о.

 

 

 

 Рис. 7. Модель заміни обладнання (устаткування)

 

Приклад практичного застосування моделі - швидкісна автострада Хансин в Японії

Перша ділянка швидкісної автостради Хансин протяжністю всього 2,3 км була побудована в 1964 р. Це була перша платна швидкісна автомагістраль в Осаке. Через два роки була відкрита швидкісна дорога в місті Кобе, що з'єднала це місто з Осакой. В середині 60-х цією дорогою щодня користувалося більше 5000 автомобілів. Цей район Японії, розташований на найбільшому острові Хонсю, є другою по населеності областю Японії (перше місце належить району Токіо). В 1992 році протяжність мережі швидкісних автомагістралей склала 200 км, щодня її послугами користувалося в середньому 828 000 автомобілів.

Середня кількість автомобілів, що припадають на одиницю площі в Японії, значно більша, ніж, наприклад, в США, де ця цифра теж не маленька.. Практично всі крупні міста Японії страждають від транспортних пробок. Вважається, що через нестачу землі пропускна спроможність дорожньої мережі ніколи не наздожене попит. Тому так важливо знайти способи максимізувати використовування дорожніх мереж, і ця задача залишиться актуальною в осяжному майбутньому. В 1970-х на швидкісній автомагістралі стала працювати автоматична система управління рухом, покликана максимізувати загальний транспортний потік, що проходить по мережі. Ідея, що лежить в основі максимізації потоку, досить складна. Може здатися, що для максимізації потоку слід дозволити всім охочим автомобілям входити в мережу і, можливо, навіть понизити платню за проїзд по трасі, щоб стимулювати попит. Але якщо допустити в швидкісну мережу дуже багато автомобілів, можуть виникнути великі пробки, що істотно зменшить потік в системі.

Одним із способів регулювання руху на магістралі Хансина є обмеження кількості автомобілів, що потрапляють на швидкісну дорогу через кожний пропускний пункт.

Максимально допустимі потоки транспорту обчислюються шляхом рішення кожні п'ять хвилин задачі лінійного програмування, що використовує дані приладів, встановлених через кожні 500 м на трасі, а також на всіх пропускних пунктах.

Метою задачі ЛП є максимізація потоку транспорту на магістралі, що автоматично приводить до максимізації доходу. На підставі рішення задачі ЛП адміністрація швидкісної автомагістралі визначає, скільком новим автомобілям можна дозволити в'їзд на трасу на кожному з пропускних пунктів. Адміністрація може також використовувати модель ЛП при виникненні дорожньо-транспортних подій (ДТП), щоб визначити, скільки автомобілів повинні покинути трасу через аварію. Щоб уникнути пробок, адміністрація автомагістралі аналізує кількість ДТП, число пошкоджених автомобілів, а також необхідний об'єм дорожніх відновних робіт. Другий метод управління рухом, що використовується, полягає в постачанні водіїв найсвіжішою і повнішою інформацією про ситуацію на швидкісній трасі і в її околицях, включаючи очікуваний час поїздки і інформацію про ДТП.

Адміністрації вдається підтримувати витрати на систему управління рухом в межах 1 % загального доходу від платні за користування швидкісною магістраллю. Найбільшою перевагою є заощаджений водіями час.

Модель ЛП для магістралі Хансина явилася прототипом для інших моделей, які використовуються в Японії і на Тайвані для організації автоматичного управління рухом і дозволяють одержати аналогічну вигоду.

ЗАВДАННЯ 3. Дослідити мережеву МОДЕЛЬ МАКСИМІЗАЦІЇ ПОТОКУ, реалізувати її у табличному процесорі MS Excel як модель ЛП і знайти розв’язок

В задачі максимізація потоку існує один вузол-джерело (вхід в систему) і один вузол стоку (вихід із системи). Ціль полягає в тому, щоб знайти, яку максимальна кількість (нафти, грошей, пакетів Інтернет, транспортних засобів) можна пропустити через дану фізичну мережу (від джерела до стоку) за одиницю часу.

Потік в одиницю часу по кожній дузі мережі обмежений її пропускною здатністю. Наприклад, діаметр трубогону обмежує потік нафти по ланках трубогінної системи. Для вузлів пропускні здатності не задаються. Єдина вимога полягає в тому, що для кожного вузла (крім вихідного і кінцевого) має виконуватись баланс потоків: потік, що виходить з вузла, має дорівнювати потоку, який входить і даний вузол.

Формулювання задачі

Анна Тарасюк - член спеціальної дослідницької групи Комісії по плануванню міського будівництва. В обов'язки групи входить узгодження будівництва нової системи підземних переходів з державним департаментом обслуговування автомагістралей. Оскільки нова система підземних переходів будується поряд з міською кільцевою дорогою, потік транспорту в східному напрямі необхідно пустити в об'їзд. Об'їзний шлях є мережею альтернативних маршрутів, запропонованих департаментом обслуговування автомагістралей. Через відмінності в обмеженнях швидкості і схемах руху пропускні спроможності різних дуг запропонованої мережі відрізняються одна від одної (рис.8).

 

Рис. 8. Пропонована мережа і пропускні спроможності різних ділянок (тис. автомобілів в годину)

Вузол 1 позначає початок об'їзду, тобто точку, в якій транспорт, що йде в східному напрямі, покидає окружну дорогу. Вузол 6 - це точка, в якій транспорт повертається на кільцеву дорогу. Пропускні спроможності на рис.8 залежать від напряму руху. Число 6 на дузі (1, 3) означає, що пропускна спроможність при русі в напрямі з вузла 1 у вузол 3 складає 6000 автомобілів в годину. Число 0 на тій же дузі означає, що при русі в напрямі з 3 в 1 пропускна спроможність рівна нулю. Це означає, що дуга (1,3) позначає вулицю з одностороннім рухом від 1 в 3. В даному прикладі вся решта дуг також позначає вулиці з одностороннім рухом.

Запропонована модель в Excel може також застосовуватися в тих випадках, коли допускається рух в обох напрямах.

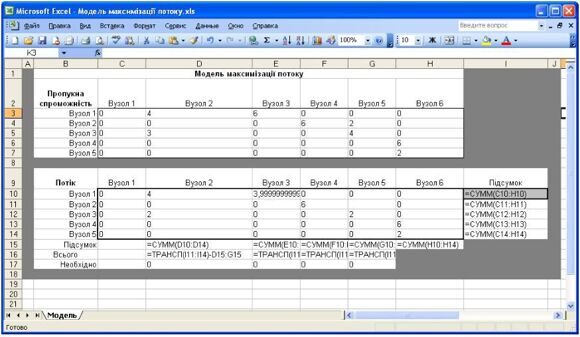
На рис.9 показана таблична модель даної мережі, в якій оптимальне рішення дозволяє знайти максимальний потік. За винятком відсутності даних про витрати, дана модель аналогічна за формою попереднім мережевим моделям. Змінні рішення (невід’ємні) в комірках С10:Н14 - це потоки з одного вузла, в інший, які не повинні перевищувати відповідні пропускні спроможності, задані в комірках СЗ:Н7. Якщо максимізувати потік, що виходить з пункту 1, то цільова функція для цього випадку записана в комірку І10. Рішення не зміниться, якщо максимізувати потік, що входить у вузол 6, тоді цільова функція міститиметься в комірку Н15. Обмеження в комірках C17:G17 вказують, що результуючий потік в кожному проміжному вузлі повинен бути рівний нулю, тобто потік, що входить у вузол, рівний потоку, що виходить з нього.

 

 

 

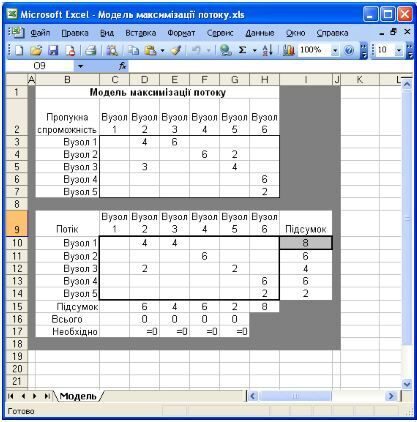
Рис. 8. Модель максимізації потоку

Як випливає із знайденого оптимального рішення, максимальний потік складає 8000 автомобілів в годину. Якщо відобразити знайдене за допомогою Excel рішення в початкову мережеву діаграму, одержимо схему руху, представлену на рис.10.

 

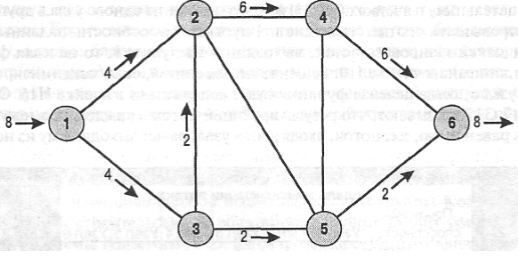
Рис. 10. Схема руху з максимальним потоком

Як це часто трапляється в мережевих моделях, в даній моделі є альтернативні оптимальні рішення, показані на рис.11.

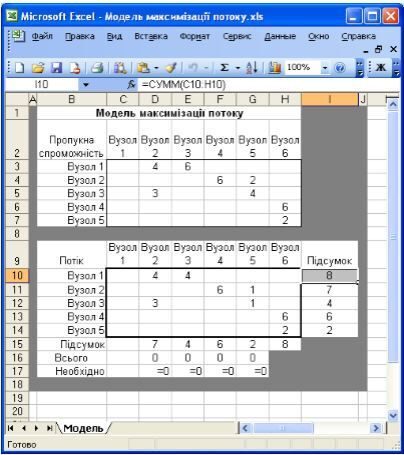
Рис. 11. Альтернативне оптимальне рішення мережевої задачі

!!!Накреслити діаграму потоків (граф) для альтернативного рішення.

Довести, що рішення не зміниться, якщо максимізувати потік, що входить у вузол 6, тоді цільова функція міститиметься в комірку Н15.