Лабораторна робота №4, Динамічна модель управління запасами

« Назад

Мета: розробити, проаналізувати модель управління запасами і реалізувати її у табличному процесорі MS Excel

ХІД РОБОТИ

Динамічні моделі управління запасами (інша назва багатофазові моделі управління запасами) складають важливий клас моделей, які застосовуються для управління запасами матеріалів, фінансів, трудових ресурсів тощо при переході від одного часового періоду до наступного.

Даний приклад - це класична детермінована "однопродуктова" модель управління запасами. Вона називається детермінованою, оскільки ми припускаємо, що на початку часового періоду 1 відомий попит (кількість замовлень, які необхідно задовольнити) для всіх подальших часових періодів.

Наприклад, виробник поліуретану має замовлення на подальші 6 тижнів. Позначимо через d_i цей відомий попит (кількість галонів продукції, яку необхідно доставити споживачам впродовж тижня i). Для простоти припустимо, що повернення замовлень неможливе, тобто d_i>0 для всіх i. Нехай С_i - витрати на виробництво галона поліуретану протягом тижня i, а K_i - максимальна кількість продукції, яка можна виробити за тиждень i. Позначимо через h_i питому вартість зберігання на складі запасів на кінець тижня i. (Таким чином, запас вимірюється як кількість галонів, перехідних з тижнів I на тиждень i+1.).

Припустимо, що початковий запас (запас на початок періоду 1, для якого не стягується платня за зберігання), складає I0 галонів. Необхідно знайти план виробництва, який дозволить задовольнити відомий попит в майбутні 6 тижнів з мінімальними загальними витратами.

Перш ніж формулювати задачу умовної оптимізації, корисно записати вираз для наявного запасу на кінець кожного періоду. Оскільки існує платня за зберігання, це кількість, очевидно, виконуватиме певну роль в цільовій функції. Позначимо через I_i (. запас поліуретану в кінці тижня i. Визначимо змінну рішення x_i як кількість галонів поліуретану, вироблену за тиждень i. Тоді рівняння матеріального балансу матиме вигляд:

I₁=I₀+x₁-d₁

Таким чином, наявний запас на кінець тижня 1 рівний наявному запасу на кінець тижня 0 (початок тижня 1) плюс вироблена за тиждень 1 кількість продукції мінус відвантажена її кількість за тиждень 1. (Передбачається, що попит повинен бути повністю задоволений. Тоді, оскільки попит на тижні i відомий і рівний d_i, таким же буде і об'єм відвантаження за тиждень i.) Аналогічно для другого тижня маємо

I₂=I₁+x₂-d₂

і для будь-якого тижня

I_i=I_i-1+x_i-d_i

Отже, рівняння запасів - це рівняння матеріального балансу:

Тут передбачається, що запас на кінець тижня t-l рівний запасу на початок тижня t, тобто не відбувається скорочення запасів. Підставивши вираз для I₁, в рівняння для I₂, одержимо

 

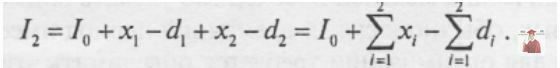
Словами це можна виразити так:

новий запас = колишній запас + виробництво - попит.

Якщо підставити одержаний вираз для I₂ в рівняння для I_i, одержимо

 

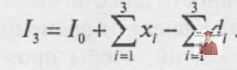
Повторюючи дану процедуру, одержуємо рівняння запасів для будь-якого тижня t

 

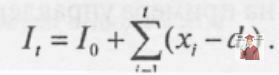
Останнє рівняння зв'язує запас на кінець тижня t з початковим запасом I₀, об'ємами виробництва за всі попередні тижні (значення х_i) і величинами попиту (значення d_i). Змінну I_t, іноді називають визначуваною змінною, оскільки вона визначається за допомогою інших змінних рішення (значень х_i) і відомих параметрів моделі. Використання визначуваних змінних іноді полегшує формулювання задач.

Перш ніж переходити до створення табличної моделі, необхідно продумати, як записати вимогу про те, щоб об'єм виробництва в кожний часовий період був достатній для задоволення попиту. Для тижня 1 це означає, що:

I₀+x_l ³ d_l або I₀+x_l - d_l ³ 0.

Оскільки вираз в правій частині останньої нерівності рівний I₁, то ця нерівність означає, що запас на кінець тижнів 1 повинен бути невід’ємним. Задоволення попиту за тиждень 2 означає, що запас на початок тижні 2 (або на кінець тижнів 1) плюс виробництво за тиждень 2 повинні бути більше d2, тобто I₁+x₂³ d2 або I₁+x₂ – d₂ ³ 0. Це еквівалентно твердженню, що запас на кінець тижня 2 повинен бути невід’ємним. Отже, видима закономірність.

Словесна модель

Мінімізувати виробничі витрати + вартість зберігання при умові запас на кінець тижня t: ³ 0, t= 1, 2,..., 6;

виробництво за тиждень t: £K_t, t - 1, 2,..., 6;

виробництво за тиждень t: ³ 0, t=l,2,..., 6.

Математична модель

Нехай х_t — об’єм виробництва за тиждень t. Математичне формулювання задачі:

мінімізувати

 

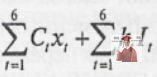
при обмеженнях

 

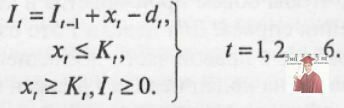
У загальному випадку пошук рішень для подібних моделей — достатньо складна задача. Необхідно враховувати взаємодії між багатьма змінними. Наприклад, запас на кінець заданого часового періоду t визначається всіма виробничими рішеннями ми для часових періодів з 1 по t. Це видно з рівняння запасів, приведеного вище. Витрати в період t також залежать від всіх виробничих рішень в періоди з 1 по t . Розглянемо практичний приклад динамічної моделі управління запасами .

Петро Артеменко відповідає за остаточну збірку і поставку дизельних електрогенераторів фірми AutoPower в Сінгапурі. Генератори збираються з деталей, що імпортуються, і випробовуються в Сінгапурі, а потім експортуються споживачам в країнах Азії.

В табл.1 показано кількість проданих генераторів, які необхідно поставляти і в кожний з подальших чотирьох місяців, а також оцінка щомісячної виробничої потужності і витрат на виробництво генераторів.

Відмінності у виробничих потужностях і витратах є слідством неритмічної доставки деталей з-за кордону і коливань цін на ринку матеріалів, зокрема, цін на мідний дріт. В табл.1 також вказана вартість зберігання готового генератора на складі під час переходу запасу від одного місяця до наступного. Витрати на зберігання великих дизельних генераторів - важливий чинник, оскільки в Сінгапурі украй обмежені земельні ресурси. Відзначимо, що саме можливість зберігати запас при переході від одного місяця до іншого робить модель динамічною моделлю, а не набором чотирьох статичних моделей, як за відсутності накопичення запасів.

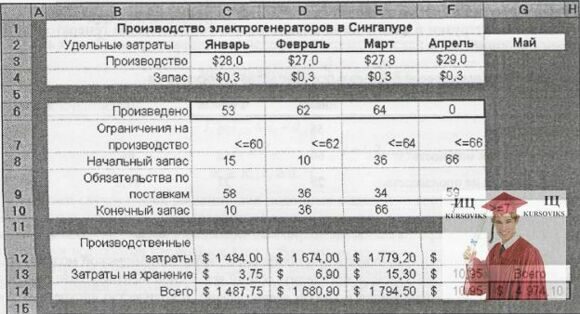
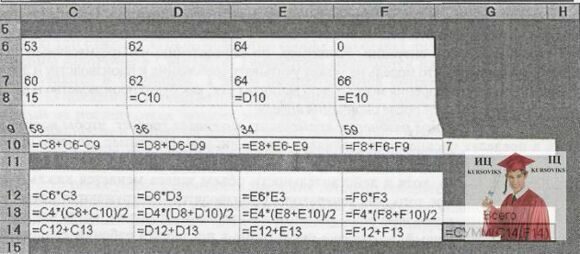
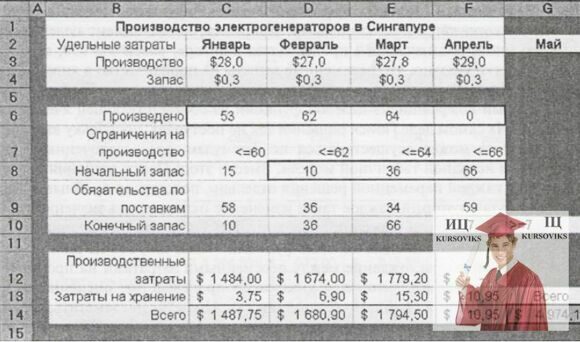
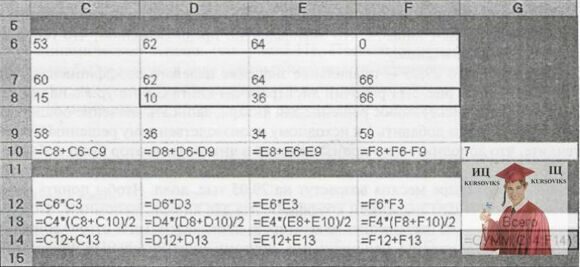
Задача Петра – забезпечити вироблення і поставку споживачам необхідної кількість генераторів в кожний з 4 місяців при мінімальних сумарних витратах за ці 4 місяці; запас на початок січня складає 15 генераторів. На рис.1 представлена таблична модель Петра Артеменка. Вона створена відповідно до загального принципу побудови динамічних табличних моделей: кожному часовому періоду відповідає окремий стовпець. В цій моделі значення кінцевого запасу в комірках C10:F10 є змінними, визначуваними. В даному випадку вони обчислюються для кожного місяця по формулі кінцевий запас = виробництво + початковий запас - поставка.

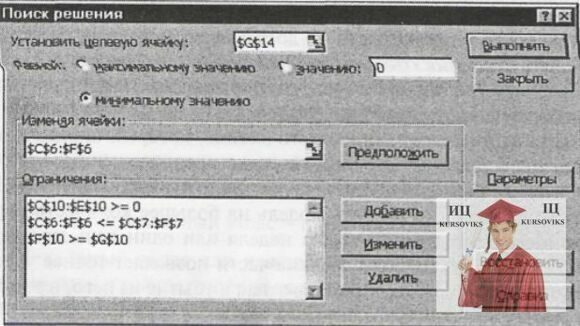
Початковий запас для кожного періоду (комірки D8:F8) рівний кінцевому запасу для попереднього періоду (комірки C10:F10). В діалоговому вікні Поиск решения необхідно додати умову невід’ємності кінцевого запасу.

Табл.1

Щомісячні дані про виробництво генераторів

 

 

 

Рис.1. Динамічна таблична модель

У даній моделі генератори із запасу не втрачаються, не ушкоджуються і не крадуться. Натомість в інших моделях управління запасами можна враховувати скорочення запасів, для чого можна ввести коефіцієнт втрат (наприклад, 1%) для кожного місяця. Це не дозволить засобу Поиск решения штучно понизити витрати шляхом відвантаження в якому-небудь місяці більшої кількості генераторів, чим є в наявності.

При побудові моделі (рівно як і при побудові будь-якої динамічної моделі) Петру необхідно ухвалити два рішення:

1. визначити загальний часовий інтервал, охоплюваний моделлю (який також називається періодом планування).

2. і кількість дискретних часових проміжків всередині даного інтервалу.

В моделі Петра період планування складає чотири місяці, і цей період поділений на чотири часових проміжки тривалістю 1 місяць. Обидва ці рішення можуть зробити визначальний вплив на відповідність моделі реальній ситуації. Наприклад, за визначенням, чотиримісячний період планування означає, що модель не може враховувати вимоги до виробництва і поставок після квітня, тобто з погляду моделі справа виглядає так, як ніби виробництво і поставка генераторів припиняються після закінчення квітня.

Крім того, щомісячне розбиття часового інтервалу вимагає, щоб всяка діяльність в межах місяця представлялася одним числом. Наприклад, кінцевий запас в січні - це виробництво за січень плюс початковий запас мінус січневі поставки, тобто однина, хоча насправді об'єм запасу міняється щодня і кожного тижня у міру того, як генератори виробляються і відвантажуються споживачам. Щоб пояснити, про що йде мова, розглянемо граничний випадок, коли всі генератори виробляються в перший, а відвантаження відбувається в останній робочий день січня.

Тоді вартість зберігання запасу в січні визначатиметься сумою виробленої кількості і початкового запасу, а не різницею цієї суми і поставленої кількості. В іншому граничному випадку, коли і виробництво і поставка відбуваються в останній робочий день січня, вартість зберігання готових генераторів залежатиме тільки від запасу на початок січня.

Припустивши для простоти, що виробництво і поставка відбуваються протягом місяця відносно рівномірно, Петро вирішив обчислювати витрати на зберігання, виходячи з середньомісячного запасу для кожного місяця, який визначається як (початковий запас + кінцевий запас) /2. Це еквівалентно припущенню, що випуск і відвантаження відбуваються в середині місяця.

Щоб точніше відобразити переміщення генераторів протягом місяця, необхідно розбити модель на більшу кількість часових проміжків (наприклад, тривалістю один тиждень або один день або навіть одна година). Розбиття часової шкали на дрібніші частини дозволяє точніше врахувати дійсні переміщення генераторів, їх перехід в запас і убування з нього, в результаті вийде точніша оцінка витрат на зберігання.

Крім використання дробового розбиття часового інтервалу для визначення щомісячних витрат, можна розширити період планування моделі, доповнивши її пов'язаними з різними видами діяльності вартісними показниками для місяців, наступних за квітнем. На жаль, спроба добитися більшого реалізму шляхом збільшення періоду планування і дрібнішого розбиття часового інтервалу приводить до експоненціального зростання розмірності динамічної моделі.

Наприклад, модель з щоденними показниками на період планування один рік міститиме сотні стовпців і швидко перевищить існуючий в Excel ліміт в 256 стовпців і можливості засобу Поиск решения (200 змінних рішення). Більш того, якщо навіть вдасться подолати ці технічні бар'єри, Петру доведеться оцінювати значення багатьох сотень параметрів, таких як щоденні вимоги по відвантаженню, витрати на матеріали і виробничі потужності по випуску генераторів. Спокусу додати моделі додатковий реалізм за рахунок дрібнішого розбиття і збільшення періоду планування в динамічних моделях називається "прокляттям розмірності". Додавання кожного нового стовпця збільшує розмір моделі, що виражається в необхідності розглядати нові змінні рішення, залежні від часу зв'язку між змінними рішення і залежними змінними, а також оцінювати додаткові параметри.

Нарешті, в кожній динамічній моделі необхідно приділяти пильну увагу граничним умовам. Йдеться про набір параметрів, для яких необхідно вказати значення на початку і в кінці часового інтервалу моделі. В моделі Петра це значення початкового запасу для січня і кінцевого запасу для квітня. В даному випадку початковий запас січня складає 15 генераторів; в загальному випадку початкове значення параметра, як правило, відоме або його легко оцінити. Проте кінцева гранична умова набагато менш надійна, оскільки вона повинне виступати в ролі розумної початкової умови для всього періоду часу, що виходить за рамки періоду планування. В даній моделі Петро вирішив, що запас на кінець квітня в 7 генераторів - достатньо хороша початкова умова для роботи в подальші місяці.

На рис. 2 представлений результат чотирикратної оптимізації моделі (окремо для кожного з чотирьох місяців). Спочатку засіб Поиск решения запускався тільки для січня, як змінна рішення використовувався об'єм виробництва в січні, а як цільова функція - січневі сумарні витрати. Потім те ж саме робилося для лютого, березня і квітня. Відзначимо, що тут немає переходів запасу від одного місяця до наступного, оскільки кожний місяць трактується як незалежна статична модель; виробництво понад об'єм поставок, який потрібен в даному місяці, приводить до збільшення загальних витрат, а компенсуючої економії в статичній моделі немає. Саме тому статичні моделі часто називають короткозорими, оскільки в них повністю ігнорується вплив поточних рішень на майбутній виграш.

Щоб побачити переваги чотиримісячної динамічної моделі в порівнянні з чотирма статичними моделями для кожного місяця окремо, порівняємо значення загальних витрат за чотири місяці на рис.1 і рис.2: застосування динамічної моделі економить значну кількість грошей.

Далі покажемо, що для даної ситуації результат, одержаний за допомогою динамічної моделі, ніколи не виявиться гіршим, а часто буде значно кращим, ніж результат запуску чотирьох статичних моделей тієї ж ситуації.

Зауваження. Розробники засобу Solver (Пошук рішення) - компанія Frontline Systems (www.frontsys.com) пропонує платні надбудови, які дозволяють розширити можливості програми, проте динамічні моделі легко можуть перевищити навіть можливості цих вдосконалених версій засобу Пошук рішення.

Числа в рядку Витрати на зберігання для січня і квітня на рис.2 відображають вартість зберігання протягом половини місяця січневого початкового запасу і необхідного квітневого кінцевого запасу.

 

Рис.2. Модель, оптимізована як чотири статичні моделі

Крім того, на перший погляд, коефіцієнти цільової функції моделі в звіті по стійкості також здаються неправильними. Наприклад, коефіцієнт цільової функції при змінній, що позначає виробництво в січні, рівний 29050 у.од., тоді як на рис. 1 чітко вказано, що змінні витрати на виробництво в січні складають 28 000у.од. Багато користувачів вважають, що засіб Поиск решения "прочитує" кожний коефіцієнт цільової функції з відповідної комірки робочого аркуша Excel. Насправді Поиск решения так не поступає, оскільки обчислення цього коефіцієнта може здійснюватися по формулах, розосереджених по декількох комірках початкової табличної моделі. Натомість Поиск решения досліджує робочий аркуш для кожної змінної рішення окремо, підставляючи пробні значення і фіксуючи результат, який кожна така зміна впливає на значення цільової функції після того, як Excel перерахує таблицю. Виходячи з цієї інформації Поиск решения оцінює коефіцієнти цільовий функции.

Саме оцінкою коефіцієнтів Пошук рішення займається в той час, коли після клацання на кнопці Виконати в рядку стану з'являється повідомлення "Постановка задачі...". На підставі одержаної інформації будується ряд Тейлора для цільової функції, потім цей ряд використовується в процесі оптимізації.

Звичайно, це не дає відповіді на питання, чому виникла розбіжність між змінними витратами на виробництво в січні і цільовим коефіцієнтом для січневого виробництва, оціненим Поиск решения і зафіксованим в звіті про стійкість. Але неважко помітити, що число 29,05 тис. у.од.. складається з витрат на виробництво генератора в січні (28,00 тис. долл.) плюс 1,05 тис. долл.- вартість зберігання даного генератора до кінця квітня (тобто протягом 3,5 місяці). Нагадуємо, що в своїй моделі менеджер використовував середні значення для оцінки рівнів запасів, це еквівалентно припущенню, що генератори випускаються в середині місяця.

Щоб переконатися, що 29,05 - правильне значення цільового коефіцієнта, можна ввести в показаний на рис.1 робочий аркуш будь-яке рішення для січня, записати значення загальних витрат за чотири місяці, а потім додати 1 до початкового виробничого рішення для січня. Ви побачите, що додатково вироблений в січні генератор буде доданий до всіх рівнів запасів, це приведе до збільшення кінцевого запасу в квітні на одиницю, а загальні витрати за чотири місяці зростуть на 29,05 тис. у.од.

Щоб зрозуміти, чому 29,05 є правильним значенням коефіцієнта для січня, нагадаємо, що вся решта елементів моделі (кількості генераторів, вироблених і відвантажених протягом інших місяців) залишилася незмінними, тому додатковий січневий генератор може потрапити тільки в кінцевий запас квітня. Проте при оптимізації моделі за допомогою Поиск решения цей додатково вироблений в січні генератор дозволяє програмі скоротити на одиницю виробництво в іншому місяці.

Наприклад, якщо додатково вироблений в січні генератор скоротить об'єм виробництва з лютому на одиницю, то результатом буде різниця між цільовими коефіцієнтами для січня і лютого, 29,05 -27,75 = 1,30 тис. у.од.

Ця різниця правильно відображає вартісний внесок двох одночасних змін, тобто перенесення виробництва одного генератора з лютого на січень підвищить витрати на виробництво на 28 000 - 27 000 = у.од.1 000 плюс 300у.од. додаткових витрат на зберігання до середини лютого генератора, виробленого в середині січня. Таким чином, дивні значення цільових коефіцієнтів, що містяться в звіті по стійкості, правильні і відображають складніші взаємозв'язки змінних рішення в динамічній моделі.

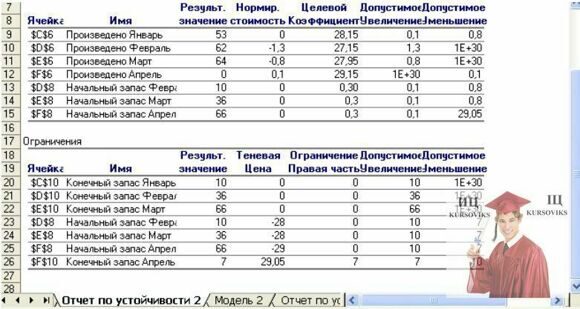
На рис.3 представлений звіт по стійкості, створений засобом Поиск решения для динамічної моделі (див. рис.1). Оскільки чотири обмеження щодо виробництва було задано у вигляді простих нерівностей, що обмежують зверху змінні рішення, тіньові ціни для даних обмежень знаходяться в звіті по стійкості в стовпці Нормована вартість, а інформація про діапазон для цих тіньових цін відсутня. Тіньова ціна – це термін, який стосується обмежень моделі і є коефіцієнтом зміни цільової функії при збільшенні правої частини даного обмеження за умови, що інші дані залишаються незмінними. В економічній теорії тіньову ціну іноді називають ціною резервування.

Рис. 3. Звіт по стійкості для моделі управління запасами за 4 місяці

На рис.4 представлена друга версія моделі Петра. Вона відрізняється від моделі на рис.1 тим, що початковий запас для кожного місяця (комірки D8:F8) є в даній моделі змінними рішення. Очевидно, щоб даний підхід мав сенс, необхідно додати певні обмеження, які не дозволять засобу Поиск решения трактувати початковий запас як рішення, незалежне від рішень щодо об'єму виробництва. В даному випадку початковий запас кожного місяця (комірки D8:F8) не повинен перевищувати кінцевий запас попереднього місяця (коміркиС10:Е10). За винятком цього невеликого ускладнення, модель на рис.4 еквівалентна початковій моделі на рис.1. Проте переваги нового формулювання стають очевидні, якщо звернутися до її звіту по стійкості (рис.5).

Рис. 5. Звіт по стійкості

Рис. 4. Модель, в якій початковий запас для кожного місяця є змінною рішення

У новому звіті по стійкості з'явилася додаткова інформація, що представляє інтерес для ухвалення рішень. Наприклад, тепер видно нечутливість сумарних витрат до змін вартості зберігання запасів, оскільки в структурі моделі на рис.5 з'явилися додаткові змінні рішення, що відображають рівень запасів, а також відповідні обмеження і, отже, - їх тіньові ціни, які відсутні, коли запас моделювався як змінні, що вводяться. Наголосимо також на ще одній позитивній властивості нової моделі: моделювання запасу у вигляді змінної рішення дозволяє розділити питомі витрати на окремі складові - виробничі коефіцієнти (питомі витрати на виробництво плюс витрати на зберігання протягом половини місяця) і коефіцієнти запасів; завдяки цьому коефіцієнти цільової функції виглядають так, як в початковій табличній версії моделі.

Формалізація моделі управління запасами у вигляді транспортної моделі

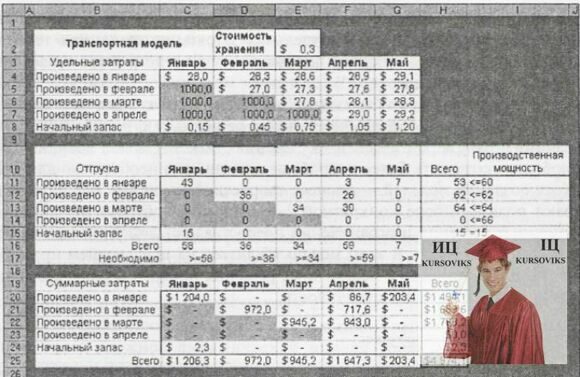
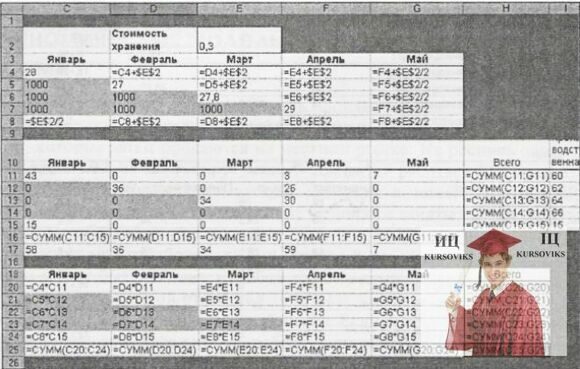
Часто динамічну модель, подібну розглянутій моделі Петра, можна сформулювати у вигляді транспортної моделі, в якій джерела (пункти відправлення) представляють рішення в певний часовий період, а пункти призначення представляють один або декілька часових періодів, на які ці рішення роблять вплив згодом. На рис.6 представлена перетворена в транспортну модель початкова модель Петра (рис.1), а також відповідне оптимальне рішення, знайдене за допомогою засобу Поиск решения. Три блоки комірок рис.6 представляють питомі витрати, рішення і сумарні витрати відповідно.

Комірки з світлим фоном в рядках з 4 по 7 представляють питому вартість виробництва генератора в заданому місяці (пункт відправлення) і доставки його певному споживачу наступного місяця (пункт призначення), включаючи вартість зберігання 300у.од. за кожний додатковий місяць. Аналогічна інтерпретація застосовується в рядку 8 для обчислення питомих сумарних витрат на зберігання початкового січневого запасу, призначеного для відвантаження наступного місяця. Відповідні рішення в блоці комірок Відвантаження представляють сумарну кількість вироблених генераторів в даному місяці (комірка Всього), в інших комірках показано, скільки генераторів з числа вироблених цього місяця призначено для відвантаження замовникам в поточному або майбутніх місяцях. Аналогічно рядок 15 показує, як розподіляється по місяцях відвантаження початкового запасу (15 генераторів). Вміст комірок C11:G15 - значення змінних рішення, знайдені засобом Поиск решения при мінімізації сумарних витрат.

Новим елементом в моделі на рис.6 є комірки з сірим фоном в блоці Питомі витрати в рядках з 5 по 7. Згідно висловленому в розділі 5.3 методу виключення неприпустимих шляхів за допомогою задання дуже великих значень вартості введення в ці осередки величезних значень питомих вартостей (1 млн.у.од.) веде до того, що Поиск решения не помістить жодного позитивного значення у відповідні комірки блоку рішень по відвантаженню (ці комірки в рядках з 12 по 14 також виділені сірим кольором). В даному випадку ці виділені комірки представляють рішення із зворотним часовим порядком дій (наприклад, вироблені в березні генератори пропонується відвантажити в минулому січні), що неможливе, тому Поиск решения повинен уникати таких решений.

Зауваження. Щоб добитися того ж ефекту іншим способом, можна залишити виділені сірим кольором комірки блоку питомих витрат незаповненими, помістити нульові значення в комірки С12, C13:DJ5 и С14:Е14 і видалити ці комірки з поля Изменяемые ячейки діалогового вікна Поиск решения.

Проте в інших обставинах виділені комірки можна використовувати для представлення складнішої ситуації, при якій допускається виконання замовлень із запізненням, наприклад, відвантаження генераторів по січневих замовленнях двома місяцями пізніше з числа вироблених в березні. У такому разі параметри питомих витрат для виділених комірок, що представляють невиконані вчасно відвантаження, відображають додаткові витрати, пов'язані з незадоволеністю клієнта, і витрати на спеціальні переговори і домовленості, викликані цією затримкою.

 

 

 

Рис. 6. Динамічна модель виробництва і управління запасами у вигляді транспортної моделі

Транспортна модель на рис.6 також має переваги в порівнянні з моделлю на рис.1. Наприклад, за допомогою моделі на рис.1 менеджер може визначити, що в січні слід виробити 53 генератори і відвантажити 58, при цьому кінцевий запас, перехідний в запас наступного місяця, складе 10 генераторів. Але що саме відбудеться з цими генераторами, як довго їх зберігати і коли відвантажувати? Цієї інформації немає в моделі на рис.1, але її легко одержати з моделі на рис.6: три з них зберігаються в запасі і відвантажуються в квітні, а що залишилися сім складуть кінцевий запас моделі, перехідний на травень. Крім того, структура моделі на рис.1 примушує вносити платню за зберігання щомісячно, а модель на рис.6 відстежує вартість зберігання для кожного генератора і дозволяє вносити цю платню в тому місяці, в якому відбувається відправлення даного генератора.

 

Рис. 7. Фрагмент звіту по стійкості для транспортної моделі менеджера Петра

В результаті графік щомісячного розподілу прямих витрат матиме інший вигляд, який більше відповідає принципам накопичувального обліку. Нарешті, представлений на рис.7 звіт по стійкості для останньої моделі значно докладніше за звіт по стійкості для попередньої моделі. Крім "сигналів" про наявність альтернативного оптимуму, даний звіт дозволяє побачити, як відіб'ється на витратах невелика зміна у вимогах до відвантаження в певному місяці, збільшення або зменшення початкового запасу січня тощо.

У цілому, перед тим, як формулювати динамічну модель, слід обдумати, що повинне бути змінною, що вводиться, а що - змінною рішення, і наскільки дрібним повинне бути часове розбиття змінних рішення. Часто ретельно продумане формулювання задачі дозволяє одержати безліч додаткової корисної інформації.