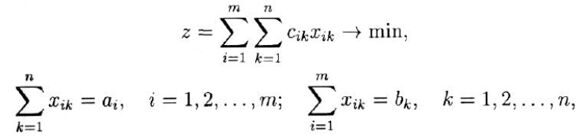Лабораторна робота №1 - Моделі лінійної оптимізації. Реалізація моделей в табличному процесорі Excel

« Назад

Мета роботи: навчитись розробляти моделі лінійної оптимізації та досліджувати їх засобами табличного процесора та його надбудови Поиск решения

ТЕОРЕТИЧНІ ВІДОМОСТІ

За допомогою моделей лінійної оптимізації розглядаються задачі, метою яких є складання оптимальних планів. Планування – це одна з основних функцій управління.

Може йтися про оптимальні плани виробництва, продажів, закупівель, перевезень, про оптимальне фінансове планування, оптимальної організації рекламної кампанії або про оптимальний план інвестиційного портфеля фірми.

Чому моделі лінійної оптимізації так важливі? Це пов'язано з тим, що дуже багато важливих для практики проблем, що відносяться до самих різних сфер діяльності, можуть бути проаналізовано за допомогою моделей лінійного програмування; існують ефективні і універсальні алгоритми рішення задач лінійної оптимізації, реалізовані в загальнодоступному програмному забезпеченні; методи аналізу моделей лінійної оптимізації дозволяють не просто одержати оптимальне рішення, але і дають інформацію про те, як може змінюватися це рішення при зміні параметрів моделі. Саме ця інформація, що дозволяє одержати відповіді на питання типу "що - якщо", представляє особливу цінність для особи, що ухвалює рішення.

При постановці будь-якої задачі оптимізації необхідно, перш за все, визначити кількісну характеристику мети, яку ми хочемо досягти в процесі оптимізації – цільову функцію. Це може бути максимум прибутки або мінімум витрат (в грошовому, часовому або якому-небудь іншому вираженні). Цільова функція показує, чому одне дане рішення краще або гірше за інше.

Цільова функція залежить від величин, званих змінними рішення. Ці величини, ми повинні змінювати, розшукуючи оптимальне рішення. Мета оптимізації знайти такі значення змінних рішення, при яких цільова функція максимальна або мінімальна. Будь-яка оптимізація завжди проводиться за наявності деяких обмежень – умов, що обмежують зміни змінних рішення.

Як вже зазначалось, задачі оптимізації називають задачами математичного програмування.

У загальному випадку задача лінійного програмування має вигляд:

,

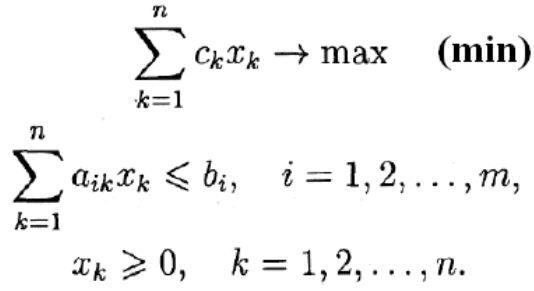де a_ik, b_k, c_i - задані числа, Х1, Х2, ..., Хn - розв’язки.

Важливий тип задач лінійного програмування представляє задача про перевезення. Називається вона так тому, що мета цієї задачі полягає в мінімізації повної вартості перевезень відомої кількості товарів зі складів до споживача.

Розглянемо так звану збалансовану транспортну задачу - задачу про перевезення, в якій загальний об'єм товарів, готових до відправлення, в точності рівний об'єму товарів, який готові прийняти в пунктах призначення.

Нехай А₁, А₂, ...,А_m — пункти відправлення, а В₁, В₂, ..., Вп — пункти призначення. Відомо, що число одиниць товару в пункті А_i дорівнює а_i, в пункті B_k — b_k,, причому

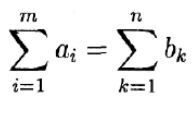
(задача сбалансована), і c_ik — вартість перевезення одиниці товару з пункту A_i в пункт В_k.

Позначимо через x_ik. (шукане) число одиниць товару, що пересилається з пункту A_i в пункт В_k.

Тоді загальна кількість товару, яку можна відправити з пункту A_i в пункти В₁, В₂, ..., В_п, дорівнює

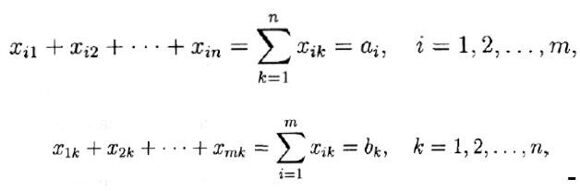a  - загальна кількість товару, яку можна прийняти в пункті В_k з пунктів А₁, А₂₂, ...,А_m.

Вартість перевезення х_ik одиниць товару з пункту А_i в пункт В_k дорівнює C_ikX_ik, а загальна вартість усіх перевезень

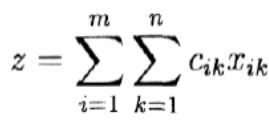В результаті отримуємо наступну модель лінійного програмування:

У загальному випадку транспортна модель – це модель ЛП, яка дозволяє знайти найдешевший спосіб задовольнити попит в n пунктах призначення, здійснюючи поставки з m відправних пунктів. Можливі такі варіанти транспортної задачі:

1) несбалансовані задачі, коли пропозиція перевищує попит;

2) несбалансовані задачі, коли попит перевищує пропозицію;

3) моделі з недопустимими шляхами;

4) з максимізацією цільової функції.

Їх формалізація потребує задання обмежень у формі нерівностей та додаткових заходів.

Якщо в транспортній задачі всі значення попиту і пропозиції є цілими, то значення змінних рішення теж будуть цілими.

Стандартна версія надбудови «Поиск решения» в MS Excel допускає розв’язання задач лінійного програмування, які містять не більше 200 змінних. Натомість існує варіант цієї надбудови, що дозволяє вирішувати задачі з десятками тисяч змінних і обмежень. Цей варіант надбудови відомий під назвою Large-Scale LP Solver. Цю просунуту надбудову можна знайти на сайті компанії-творця цього інструменту FrontLine System www.solver.com. Надбудову можна скачати безкоштовно і користуватися нею протягом двотижневого пробного терміну.

Завдання 1. Розробити і реалізувати модель лінійної оптимізації для наведеної задачі Поставки двох видів продуктів

Менеджер відділу логістики складає план перевезень продукції фірми з 3 її складських комплексів База 1, База 2, База 3 до чотирьох клієнтів: X, У, Z і W.

Йдеться про перевезення двох видів продукції: А і B.

Вартість перевезень для кожного вигляду продукції, виходячи з відстаней і інших обставин, дані в таблиці.

Клієнти замовляють наступні кількості товарів A, B.

На базах у даний час є такі запаси:

Складіть план перевезень, що мінімізує транспортні витрати, проведіть дослідження найгіршого плану перевезень.

Для рішення задачі використайте два підходи. Порівняйте отримані результати і зробіть висновки.

Завдання 1.1. Перший підхід достатньо очевидний - потрібно розділити задачу на дві, по числу продуктів, призначених для перевезення. Кожну з двох задач при цьому розв'яжіть звичайним способом.

Завдання 1.2. Другий підхід припускає отримання рішення в одній моделі. Це може бути виправдано, якщо перевезення різних вантажів будуть якось пов'язані один з одним.

 

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО РЕАЛІЗАЦІЇ ДРУГОГО ПІДХОДУ

Як завжди, перш ніж будувати таблицю для вирішення задачі, перевіримо баланс. Загальна кількість вантажу в запасах 191 од., загальна кількість замовленого вантажу - 191 од. Загальний баланс є. Але в цій задачі є два види вантажів, і загальний баланс може не відображати балансів окремих продуктів. Тому в даному випадку нам доведеться перевіряти баланс по кожному продукту окремо. Тепер задача виявляється не збалансованою по обох продуктах:

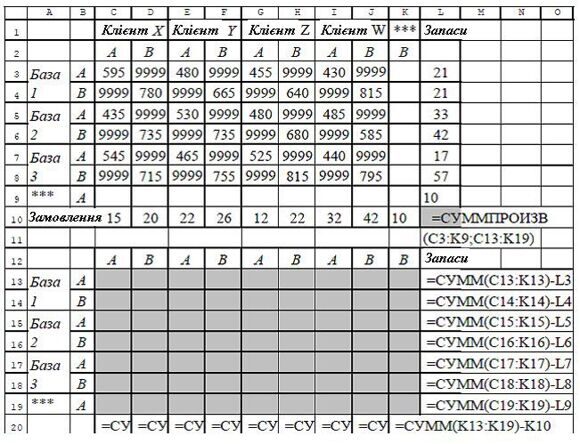
продукту А є в запасах 71 од., а замовлено клієнтами 81 од., продукту B в запасах 120 од., а замовлено клієнтами 110 од. Отже задачу доведеться балансувати штучно. Продукту А не вистачає для задоволення клієнтів, значить потрібно додати фіктивного постачальника із запасом продукту А в 10 одиниць. Продукт В є в надлишку, тому потрібен додатковий клієнт, який замовить 10 одиниць, що залишилися. Щоб не захаращувати таблицю, вважатимемо, що фіктивний постачальник має тільки продукт А, а фіктивний клієнт замовляє тільки продукт В. В цьому випадку ми одержимо наступну таблицю (рис. 1). В даній задачі як цільову функція розумно вибрати повні витрати по перевезеннях. Підрахуємо їх по формулі =СУММПРОИЗВ(C3:K9;C13:K19), де таблиця C3:K9 містить ціни перевезень, а таблиця змінних C13:K19 - кількості вантажів, що перевозяться по кожному з допустимих маршрутів. Метою оптимізації, зрозуміло, вибираємо пошук мінімуму.

У рядку C20:K20 підраховуємо баланс виконання замовлень, а в стовпці L13:L19 - баланс вивозу запасів. У принципі, можна б було ставити задачу Пошуку рішення, але давайте ще раз подивимося таблицю цін перевезень. В початковій таблиці цін порожні комірки означали відсутність відповідного перевезення. Наприклад, порожня комірка D3 показує, що ніякого перевезення, здатного при відвантаженні одержати 1 одиницю продукту А з бази 1, а доставити 1 одиницю продукту В клієнту Х не існує. Проте для надбудови Поиск решения порожня комірка означає нульову ціну і такі перевезення будуть заплановані. Тому нам слід заборонити всі подібні перевезення.

Як і в звичних задачах заборонити перевезення по маршруту можна, поставивши високу ціну перевезення. Давайте додамо в таблицю цін довільне число, набагато більше будь-якої з наявних цін, в кожну з тих, що залишилися порожніми осередків.

Рис.1

Мінімальна загальна вартість перевезень складе 104 760 грн.

Щоб перевірити, наскільки одержаний при оптимізації план кращий, ніж інші можливі плани, пошукаємо план, що приносить максимум витрат. Для цього потрібно буде модифікувати таблицю цін. Адже ми ставили велику ціну перевезення для заборони деяких маршрутів, а при пошуку максимуму таку заборону можна реалізувати, тільки поставивши низьку ціну. Простіше всього це зробити через меню Правка\Заменить … -> Найти: 9999,

Замінити на: -9999, Замінити все.

Після заміни запускаємо Поиск решения знов змінюємо мету пошуку на максимум.

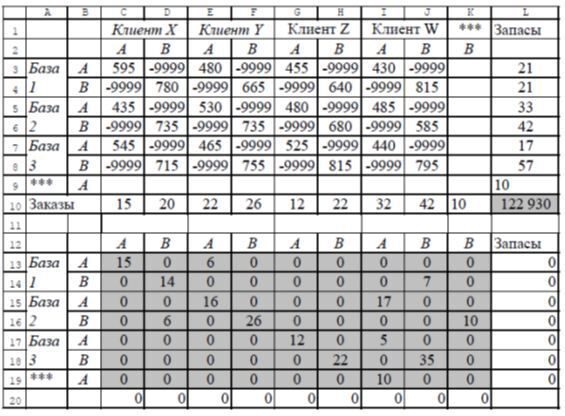Рис.2

У одержаному рішенні (рис. 2) сумарна вартість перевезень зростає до 122930 грн Таким чином, найгірший план відрізняється від кращого менше ніж на 20%, що дає певну свободу вибору серед можливих планів перевезень.