Задачі з Економічної кібернетики - Екзаменаційні задачі (24 штук)
Код роботи: 537
Вид роботи: Задачі
Предмет: Економічна кібернетика
Тема: Екзаменаційні задачі (24 штуки)
Кількість сторінок: 50
Дата виконання: 2015
Мова написання: українська
Ціна: 2500 грн за усі задачі (і по 150 грн за 1 штуку)
ВАРІАНТ №1
Задана технологічна матриця (матриця коефіцієнтів прямих матеріальних витрат галузей):
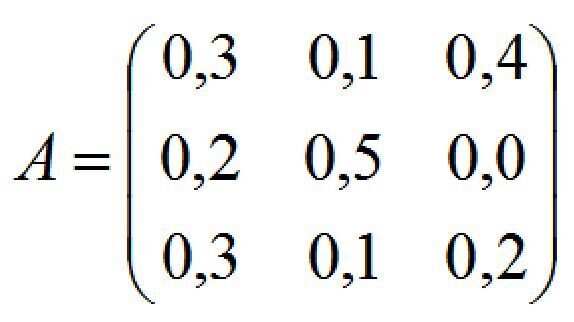Чи здатна економічна система забезпечити невід’ємний кінцевий випуск у всіх галузях?
ВАРІАНТ №2
Задана технологічна матриця (матриця коефіцієнтів прямих матеріальних витрат галузей):
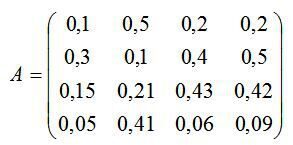
Чи здатна економічна система забезпечити невід’ємний кінцевий випуск у всіх галузях?
ВАРІАНТ №3
Задана технологічна матриця (матриця коефіцієнтів прямих матеріальних витрат галузей):
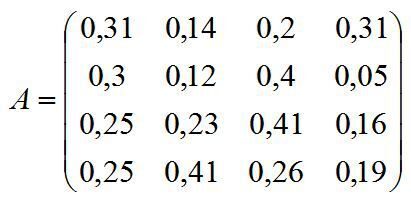
Чи здатна економічна система забезпечити невід’ємний кінцевий випуск у всіх галузях?
ВАРІАНТ №4
Задана технологічна матриця (матриця коефіцієнтів прямих матеріальних витрат галузей):
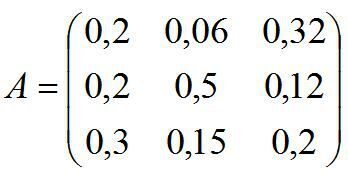
Чи здатна економічна система забезпечити невід’ємний кінцевий випуск у всіх галузях?
ВАРІАНТ №5
Задана технологічна матриця (матриця коефіцієнтів прямих матеріальних витрат галузей):
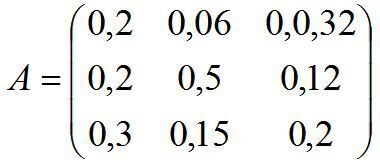
Чи здатна економічна система забезпечити невід’ємний кінцевий випуск у всіх галузях?
На основі мережевої діаграми скласти математичну модель оптимізації перевезень.
ВАРІАНТ №6
На основі мережевої діаграми скласти математичну модель оптимізації перевезень
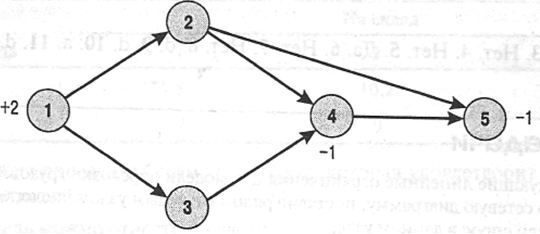
ВАРІАНТ №7
На основі мережевої діаграми скласти математичну модель оптимізації перевезень
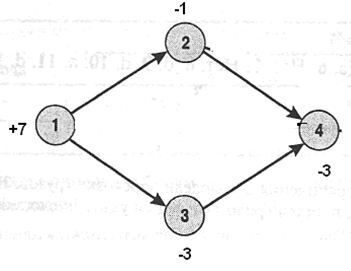
ВАРІАНТ №8
На основі мережевої діаграми скласти математичну модель оптимізації перевезень
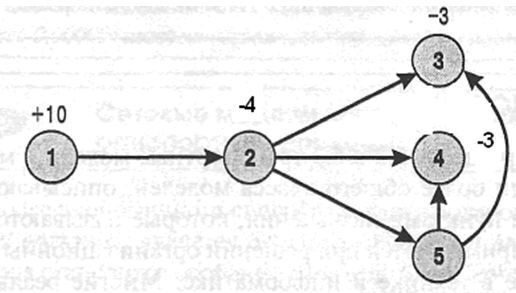
ВАРІАНТ №9
На основі мережевої діаграми скласти математичну модель задачі оптимізації перевезень
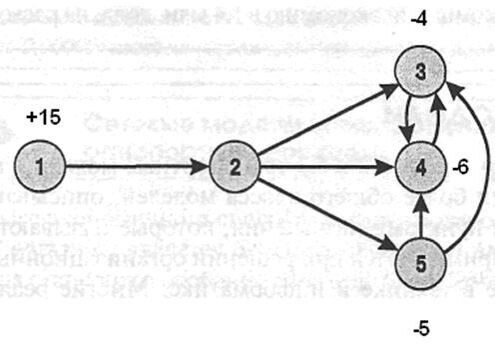
ВАРІАНТ №10
На основі мережевої діаграми скласти математичну модель задачі оптимізації перевезень
ВАРІАНТ №11
На основі мережевої діаграми скласти математичну модель задачі оптимізації перевезень
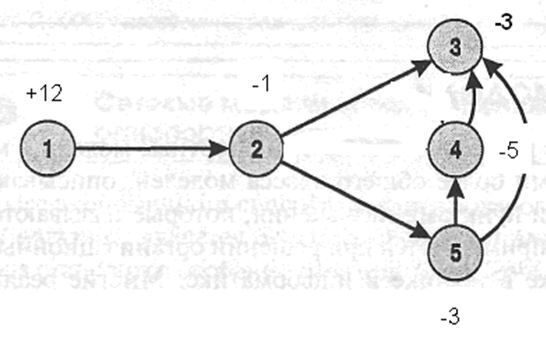
ВАРІАНТ №12
Побудувати МОДЕЛЬ - виробничу функцію Кобба-Дугласа: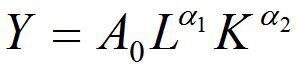 
за заданими статистичними даними, перевірити модель на адекватність статистичним даним. Для побудови моделі застосувати засоби MS Excel.
|
№ з/п |
L |
K |
Y |
|
1 |
44,4 |
33,3 |
52,6 |
|
2 |
47,3 |
38,5 |
59,0 |
|
3 |
48,2 |
40,4 |
61,3 |
|
4 |
49,8 |
45,8 |
66,5 |
|
5 |
52,2 |
46,2 |
68,1 |
|
6 |
54,3 |
50,0 |
72,3 |
|
7 |
54,4 |
52,1 |
74,8 |
|
8 |
56,9 |
56,7 |
79,6 |
|
9 |
58,7 |
57,9 |
81,9 |
|
10 |
61,5 |
60,5 |
84,6 |
ВАРІАНТ №13
Для заданої функції корисності споживача
U(X1,X2)=(X1+2)(2X2+5),
де X1, X2 - кількість споживаних товарів двох різновидів,
1) запишіть рівняння лінії байдужості, яка проходить через точку (2, 3), побудуйте криву байдужості.
2) знайдіть граничну корисність кожного різновиду товарів.
ВАРІАНТ №14
Для заданої функції корисності споживача
U(X1,X2)=(3X1+1)(X2+5),
де X1, X2 - кількість споживаних товарів двох різновидів,
1) запишіть рівняння кривої байдужості, яка проходить через точку (1, 2), побудуйте криву байдужості;
2) побудуйте лінію бюджетного обмеження за умови, що бюджет споживача становить 1500 грн, ціна першого товару – 55 грн, а другого – 150 грн.
ВАРІАНТ №15
Для заданої функції корисності СПОЖИВАЧА
U(X1,X2)=(4X1+1)(3X2+1),
де X1, X2 - кількість споживаних товарів двох різновидів.
Знайдіть точку споживчої рівноваги за умови, що бюджет споживача становить 3500 грн, ціна першого товару – 65 грн, а другого – 135 грн.
ВАРІАНТ №16
Для тригалузевої економічної системи задані матриця коефіцієнтів прямих матеріальних витрат А і вектор кінцевої продукції Y:
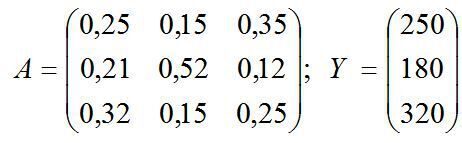
Обчислити вектор валової продукції.
ВАРІАНТ №17
Побудувати матрицю коефіцієнтів повних матеріальних витрат за даними таблиці. Перевірити модель міжгалузевого балансу на продуктивність.
|
Галузь |
Прямі міжгалузеві потоки |
Кінцева продукція |
||
|
1 |
2 |
3 |
||
|
1 |
50 |
60 |
80 |
60 |
|
2 |
25 |
90 |
40 |
25 |
|
3 |
25 |
60 |
40 |
35 |
ВАРІАНТ №18
Побудувати матрицю коефіцієнтів прямих і повних матеріальних витрат за даними таблиці. Перевірити модель міжгалузевого балансу на продуктивність.
|
Галузь |
Прямі міжгалузеві потоки |
Кінцева продукція |
||
|
1 |
2 |
3 |
||
|
1 |
250 |
160 |
80 |
210 |
|
2 |
125 |
90 |
140 |
175 |
|
3 |
75 |
110 |
60 |
135 |
ВАРІАНТ №19
Для заданої функції корисності споживача
U(X1,X2)=2X1+3X2,
де X1, X2 - кількість споживаних товарів двох різновидів,
3) запишіть рівняння кривої байдужості, яка проходить через точку (2, 3), побудуйте криву байдужості.
4) знайдіть граничну корисність кожного різновиду товарів.
ВАРІАНТ №20
Для заданої функції корисності споживача
U(X1,X2)=3X1+4X2,
де X1, X2 - кількість споживаних товарів двох різновидів,
1) запишіть рівняння кривої байдужості, яка проходить через точку (1, 2), побудуйте криву байдужості;
2) побудуйте лінію бюджетного обмеження за умови, що бюджет споживача становить 1500 грн, ціна першого товару – 55 грн, а другого – 150 грн.
ВАРІАНТ №21
Для заданої функції корисності споживача
U(X1,X2)=4X1+3X2,
де X1, X2 - кількість споживаних товарів двох різновидів.
Знайдіть точку споживчої рівноваги за умови, що бюджет споживача становить 3500 грн, ціна першого товару – 65 грн, а другого – 135 грн.
ВАРІАНТ №22
Для заданої функції корисності споживача
U(X1,X2)=3X1+2X2,
де X1, X2 - кількість споживаних товарів двох різновидів,
1) запишіть рівняння кривої байдужості, яка проходить через точку (2, 3), побудуйте криву байдужості.
2) знайдіть граничну корисність кожного різновиду товарів.
ВАРІАНТ №23
Для заданої функції корисності споживача
U(X1,X2)=5X1+3X2,
де X1, X2 - кількість споживаних товарів двох різновидів,
1) запишіть рівняння лінії байдужості, яка проходить через точку (1, 2), побудуйте криву байдужості;
2) побудуйте лінію бюджетного обмеження за умови, що бюджет споживача становить 1500 грн, ціна першого товару – 55 грн, а другого – 150 грн.
ВАРІАНТ №24
Для заданої функції корисності СПОЖИВАЧА
U(X1,X2)=4X1+3X2,
де X1, X2 - кількість споживаних товарів двох різновидів.
Знайдіть точку споживчої рівноваги за умови, що бюджет споживача становить 3500 грн, ціна першого товару – 65 грн, а другого – 135 грн.