Лабораторна робота №4, Дискретні моделі економічної динаміки

Мета: набути теоретичних знань та практичних навичок аналізу дискретних моделей економічної динаміки.

Хід роботи

Створіть документ Lab_№5_Прізвище.xls. В ньому виконайте завдання 3-5. Кожна модель – на окремому робочому аркуші, аналіз – у рухомому текстовому блоці.

Скористайтесь методичними рекомендаціями. Завдання 1-2 виконайте письмово у робочому зошиті.

Завдання 1. Знайдіть загальний розв’язок різницевих рівнянь:

1) 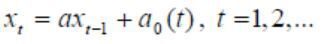, де a=0,2n, a₀=3n

2) 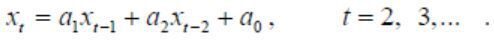, де a₁=2n , a₂=-n, a₀=2.

Завдання 2. Знайдіть загальний розв’язок системи різницевих рівнянь:

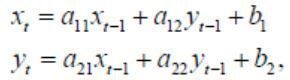
де a₁₁=-2n, a₁₂=n, a₂₁=-2n+3, a₂₂=-n+12.

Завдання 3. Дослідіть дискретну модель Кейнса за умов:

1) схильність до споживання с=0,5 для n=1:5; с=0,6 для n=6:10; с=0,4 для n=10:15; с=0,7 для n=15:20;

2) нижня межа споживання становить 7n;

3) внутрішні інвестиції зростають лінійно за законом І_t=0,2t+12;

4) побудуйте фазовий портрет системи для t=1:100, проаналізуйте.

Завдання 4. Дослідіть дискретну модель Харрода-Домара за умов:

1) схильність до споживання с=0,5 для n=1:5; с=0,6 для n=6:10; с=0,4 для n=10:15; с=0,7 для n=15:20;

2) коефіцієнт акселерації r=0,1 для n=1:5; r=0,2 для n=6:10; r=0,3 для n=10:15; r=0,4 для n=15:20;

3) побудуйте фазовий портрет системи для t=1:100, проаналізуйте.

Завдання 5. Дослідіть дискретну модель мультиплікатора-акселератора на прикладі моделі Самуельсона-Хікса за умов:

1) схильність до споживання с=0,5 для n=1:5; с=0,6 для n=6:10; с=0,4 для n=10:15; с=0,7 для n=15:20;

2) коефіцієнт акселерації r=0,1 для n=1:5; r=0,2 для n=6:10; r=0,3 для n=10:15; r=0,4 для n=15:20;

3) нижня межа споживання становить 7n;

4) внутрішні інвестиції зростають лінійно за законом І_t=0,2t+12;

5) побудуйте фазовий портрет системи для t=1:100, проаналізуйте.