Лекция №3, Аналитическое (количественное) моделирование

« Назад

1. Принципы решения хорошо структурированных проблем

Использование математического моделирования для описания систем различной сложности обусловлены тем, что математическое описание в сравнении с словесным (вербальным) является более компактны и ясным. Использование математического описания позволяет каждому аспекту изучаемого процесса поставить в соответствие определенный математический символ, в результате чего становится нагляднее взаимосвязь, существующая между различными параметрами процесса. Математическая модель дает основу для численного анализа, с помощью которого могут быть получены данные не только описательного, но и прогностического характера.

Хорошо структурированная проблема характеризуется следующими особенностями:

- цель предстоящих действий объективна, т.е. задана извне и никак не зависит от менеджера;

- варианты решения (альтернативы) известны, нужно лишь выбрать лучший;

- перечень необходимых ресурсов известен, надо лишь обосновать нужное их количество для решения проблемы;

- факторы, которые необходимо учитывать при решении проблемы поддаются точному количественному учёту в виде числа или функции;

- функции между переменными объективны и могут быть получены.

Для решения хорошо структурированных проблем , т.е. для построения математических моделей имеется мощный математический аппарат (математический анализ, функциональный анализ, исследование операций, теория вероятностей, математическая статистика, теория массового обслуживания и т.д.).

Количественные методы предоставляют мощные инструменты анализа в области экономики и решают следующие задачи:

1) задачи распределения ресурсов (планирование производства);

2) задачи выбора маршрута (транспортные задачи);

3) задачи оптимального управления запасами;

4) задачи ремонта и замены оборудования;

5) задачи сетевого планирования сложных проектов;

6) задачи массового обслуживания.

Количественные методы дают четкие и ясные ответы на точно поставленные вопросы. Они позволяют просчитать последствия выбора различных альтернатив и выделить наилучшую по тому или иному критерию. Однако сами по себе количественные методы вопросов не ставят, критерии не выбирают и решений не принимают. Это – задача менеджеров.

Весь набор задач можно разбить на две части: «Оптимизация в условиях полной определенности» и «Принятие решений в условиях неопределенности и риска», содержащие следующие разделы.

I. Оптимизация в условиях полной определенности включает (математическое программирование):

1. Метод линейной оптимизации;

2. Транспортные задачи и логистика; задачи о назначениях и отборе;

3. Оптимальное управление запасами;

4. Планирование и анализ проектов (сетевое моделирование).

II. Принятие решений в условиях неопределенности и риска:

6. Управление проектами с учетом случайных вариаций времени выполнения (сетевое моделирование, теория графов);

7. Оптимальное управление запасами с учетом случайных вариаций спроса;

8. Выбор альтернатив (теория игр);

9. Оценка эффективности систем массового обслуживания и их оптимизация (имитационное моделирование, модели теории очередей).  

2. Оптимизация в условиях полной определенности

Рассмотрим примеры применения количественных моделей и методов, цель которых найти оптимальную стратегию управления (или, хотя бы рассчитать результат при выбранной стратегии управления) в условиях, когда все параметры и правила функционирования управляемой системы четко определены и не подвержены никаким случайным воздействиям.

В реальной жизни вряд ли может существовать “полная определенность”. Однако, несмотря на то, что жизнь полна случайностей, сложна и неоднозначна, часто возникают ситуации, когда мы склонны игнорировать случайность. В некоторых ситуациях, случайные воздействия на интересующий нас процесс управления не учитываются потому, что они малы и несущественны. В других ситуациях, случайные факторы, которые могут оказать сильное и негативное влияние на нашу деятельность (поломки оборудования, катастрофы, социальные потрясения и т.п.), к счастью, происходят достаточно редко.

Широко используемым методом является метод линейной оптимизации. С помощью моделей линейной оптимизации рассматриваются задачи, целью которых является составление оптимальных планов производства, продаж, закупок, перевозок, об оптимальном финансовом планировании, оптимальной организации рекламной кампании или об оптимальном плане инвестиционного портфеля фирмы.

При постановке любой задачи оптимизации необходимо, прежде всего, определить количественную характеристику цели, которую мы хотим достичь в процессе оптимизации – целевую функцию. Это может быть максимум прибыли или минимум издержек (в денежном, временном или материальном выражении). Целевая функция показывает, почему одно рассматриваемое решение лучше или хуже другого.

Целевая функция зависит от величин, называемых переменными решения. Эти величины, мы должны изменять, разыскивая оптимальное решение. Цель оптимизации найти такие значения переменных решения, при которых целевая функция максимальна или минимальна.

Любая оптимизация всегда проводится при наличии некоторых ограничений – условий, ограничивающих изменения переменных решения при поиске максимальной или минимальной целевой функции. Эти ограничения могут диктоваться:

- вторичными целями (например, минимизируя риск инвестиционного портфеля, мы одновременно хотим добиться ожидаемой прибыли не хуже заданной);

- ограниченностью ресурсов, находящихся в нашем распоряжении (денежных, временных, материальных);

- установленными «правилами игры» (рыночные ограничения, нормативные акты, лимитирующие ту или иную характеристику или любые требования субъекта, принимающего решения).  

2.1. Почему модели линейной оптимизации столь важны?

Это связано с тем, что очень много важных для практики проблем, относящихся к самым разным сферам деятельности, могут быть проанализированы с помощью моделей линейного программирования; существуют эффективные и универсальные алгоритмы решения задач линейной оптимизации, реализованные в общедоступном программном обеспечении; методы анализа моделей линейной оптимизации позволяют не просто получить оптимальное решение, но и дают информацию о том, как может изменяться это решение при изменении параметров модели для лица, принимающего решение.

Линейная оптимизация имеет дело с моделями, в которых целевая функция линейно зависит от переменных решения, и ограничения представляют собой линейные уравнения или неравенства относительно переменных решения. Фактически, это означает, что целевая функция и ограничения могут представлять собой только суммы произведений постоянных коэффициентов на переменные решения в первой степени, т.е. выражения типа:

c1х1 + с2х2 + … + сnxn 

2.2. Транспортная задача

Классическая транспортная задача имеет целью минимизацию транспортных издержек при перевозках однотипных грузов от нескольких поставщиков (с различных складов), расположенных в разных местах, к нескольким потребителям.

При постановке транспортной задачи необходимо задать таблицу транспортных издержек для перевозок единицы груза cij от i- го поставщика к j-му потребителю. Эта таблица имеет m строк (по числу поставщиков) и n столбцов (по числу потребителей). Необходимо также задать запасы поставщиков, готовые к вывозу (аi) и величины заказов потребителей (bj).

В транспортной задаче предполагается, что необходимо вывести запасы каждого i-го поставщика и удовлетворить заказ каждого j-го потребителя. Это возможно только если сумма запасов всех поставщиков равна сумме заказов всех потребителей. Это важнейшее условие применимости эффективных алгоритмов, условие сбалансированности.

Таблица перевозок xij имеет те же размеры (m х n) и содержит переменные решения.

Чтобы получить целевую функцию (суммарные издержки перевозок), необходимо найти сумму произведений матрицы транспортных издержек на матрицу перевозок. При этом номер источника (поставщика), 1…i<=m, номер пункта назначения (потребителя), 1…j<=n: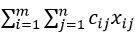 

Ограничения транспортной задачи имеют очень простой вид: сумма переменных решения вдоль каждой i-ой строки должна быть равна запасу поставщика ai, а сумма переменных решения вдоль каждого j-го столбца должна быть равна заказу соответствующего потребителя bj.

Если задача сбалансирована и никаких других ограничений, кроме упомянутых выше нет, поиск решения использует эффективный алгоритм решения для этой задачи. Причем, если запасы и заказы выражены целыми числами, то и переменные решения xij получатся целыми, даже если не требовать этого специально. Кроме того, гарантировано, что количество ненулевых перевозок xij не будет превышать m+n-1, т.е. количество «игроков» (поставщиков и потребителей) минус 1.  

2.3. Несбалансированность в транспортной задаче

Если сумма запасов превышает сумму заказов (излишек запасов) или, наоборот сумма запасов меньше, чем сумма заказов (дефицит запасов) необходимо сбалансировать задачу.

В первом случае, нужно добавить в таблицу транспортных издержек и в таблицу перевозок по одному лишнему столбцу.

Это можно трактовать так, как если бы появился еще один «фиктивный» потребитель. Если потребовать, чтобы заказ этого «потребителя» в точности равнялся бы разности между суммой всех запасов и суммой всех заказов издержки перевозок грузов к нему от любого поставщика равны нулю, будем иметь сбалансированную транспортную задачу. При этом переменные решения в последнем столбце дадут количество грузов, которые должны остаться на каждом из складов.

Во втором случае, когда нужно добавить в таблицу транспортных издержек и в таблицу перевозок по одной лишней строчке.

Это можно трактовать так, как если бы появился еще один «фиктивный» поставщик. Потребуем, чтобы запас этого «поставщика» в точности равнялся бы разности между суммой всех заказов и суммой всех запасов, а издержки перевозок грузов от него к любому поставщику равны нулю. Вновь имеем сбалансированную транспортную задачу. При этом переменные решения в лишней строчке – это тот объем грузов, которые не получит каждый потребитель.

Заметим, что несбалансированные транспортные задачи можно, конечно, решать и просто заменив в соответствующих ограничениях знаки равенств на знаки нестрогих неравенств. Однако, при этом надо иметь в виду, что для решения такой задачи MS-Excel будет применять общие методы решения ЛП задач, а не специфические «транспортные» алгоритмы. В результате эффективность решения может быть значительно ниже, и получение целочисленного решения не гарантируется. 

2.4. Оптимальное управление запасами

Модели управления запасами используются для определения времени размещения заказов на ресурсы и их количества, а также массы готовой продукции на складах. Цель данной модели – оптимизация запасов на предприятии. Чрезмерное их накопление помогает избежать потерь, обусловленных их нехваткой, во многих случаях сводит к минимуму издержки на размещение заказов, так как они размещаются в больших количествах, но также ведет к дополнительным издержкам на хранение, перегрузку, потери от порчи, уменьшение оборотных средств, что уменьшает мобильность предприятия в принятии решений при возникновении новой ситуации на рынке.

Рассматривается модель фиксированного размера заказа, которая предполагает, что восполнение запаса происходит периодически, и при этом каждый раз размер заказа один и тот же. Модель определяет оптимальный размер заказа из соображений минимума суммы издержек хранения и издержек заказа за 1 год, тем самым, задавая средний уровень запаса данного товара на складе и частоту его заказов у поставщика.

Издержки хранения должны быть прямо пропорциональны количеству единиц хранимых запасов и стоимости единицы запаса. Основную часть этих издержек составляют упущенные возможности при альтернативном использовании капитала, «замороженного» в запасах.

Будем использовать для обозначения таких удельных издержек хранения либо большую букву H, либо маленькую букву h, полагая, что это процент от стоимости единицы запаса C при хранении этой единицы в течение года. Тогда, суммарные предельные издержки хранения всегда будут пропорциональны количеству хранимых единиц запаса и времени хранения с коэф. пропорц. H (h*C):

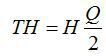
Издержки по запуску появляются, когда речь идет о новой партии продукции (производство) или затраты на формирование и оформление заказа (торговля).

Эти издержки не зависят от величины предполагаемой партии продукции (заказа). В торговле их чаще всего связывают, с оплатой труда менеджеров, «ведущих» этот заказ, с контролем погрузки – разгрузки, с офисными расходами при оформлении и размещении заявки поставщику на новый заказ и др.

В производстве этим постоянным издержкам соответствуют затраты на переналадку оборудования для выпуска данной партии продукции. Величину этих издержек, в расчете на один заказ (или на одну переналадку производственной линии) принято обозначать буквой S.

Эти издержки постоянные в том смысле, что S не зависит непосредственно от размера партии продукции данного наименования. Однако, чем больше размер заказа, тем реже приходится оплачивать расходы на его оформление, тем меньше затраты на оформление заказов (или на переналадку оборудования) за выбранный базовый период (год, месяц и т.п.):

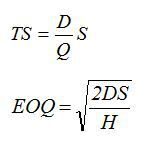
Пример 6.

Машиностроительный завод покупает болты с гайками для сборочного участка, годовая потребность в которых составляет 50 тыс. штук в год. На данный момент имеется два предложения от разных поставщиков, условия которых приведены в таблице. 

Поставщик А		Поставщик В
Кол-во	Цена за шт., руб.	Кол-во	Цена за шт., руб.
до 5000	5	до 9999	4.8
5000 - 19999	4.6	10 000 - 29 999	4.5
от 20 000	4.4	от 30 000	4.3

Стоимость хранения для завода можно оценить в 38% от стоимости единицы товара в год. Стоимость оформления одного заказа – 1000 руб. Спрос в течение года на данные болты равномерный.

a. Каков оптимальный размер заказа с учетом скидок каждого из поставщиков.

b. Какого поставщика следует предпочесть? 

Решение.

Спрос на болты по условию задачи известный и постоянный, следовательно, мы можем без ограничений использовать модель экономичного размера заказа EOQ. При этом все издержки будут определяться полными издержками хранения и заказа за год. Однако имеется система скидок на базовые цены, а это значит, что отклонение от экономичного размера заказа может оказаться выгодным, если полученные скидки превышают рост издержек хранения. Значит к сумме издержек хранения и заказа нужно добавить общие затраты на покупку болтов, чтобы иметь возможность корректно сравнивать разные предложения.

Так как в данной задаче нам необходимо рассчитать оптимальный заказ для шести цен и количественных диапазонов (2 поставщика и 3 диапазона действия цен у каждого) организуем данные, как показано в таблице (Рис. 29). В верхних ячейках A2:C2 запишем общие данные: издержки хранения, издержки заказа и годовую потребность. В строках B4:G4 и B5:G5 запишем верхние и нижние границы диапазонов скидок. Число 1 млн. в ячейках D4 и G4 заменяет бесконечную границу диапазона и выбрано произвольно, для упрощения формул. 

Для расчета экономичного размера заказа используем стандартную формулу 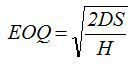(формула Уилсона). В нашей задаче величина H непостоянна, так как она зависит от цены товара, а цена может быть разной. Поэтому в расчетах вместо самой величины H будем использовать ее выражение через цену и издержки хранения в процентах h: H=h*C. С этой поправкой формула для EOQ и записана в ячейке B7. Ссылки на издержки хранения h, годовую потребность D и издержки заказа S фиксированы, для удобства протягивания формулы вправо, для расчета EOQ для других цен закупки. После протягивания формулы получаем следующий результат (Рис. 30). 

Если мы теперь сравним полученные значения EOQ с диапазонами количеств закупаемых болтов, для которых действуют те цены, по которым мы считали EOQ, то обнаружим несколько несоответствий. Например, при покупке болтов у поставщика A по цене 5 руб. за штуку оптимальная величина заказа равна примерно 7255 штук. Но такая цена действует только при покупке менее 5000 штук. Если мы будем закупать болты партиями по 7255 штук, то их цена будет только 4.6 руб. Это конечно неплохо, но мы ведь хотели выяснить, какую партию болтов лучше всего выбрать, если покупать их по цене 5 руб.!

Ясно, что выбирать размер партии мы должны только внутри диапазона от 1 до 5000 штук. Какой же размер выбрать? Здесь нужно вспомнить, как выглядит график зависимости суммы издержек хранения и заказа от размера заказа. А именно, график этот показывает гладкую функцию без перегибов с одним минимумом. Это значит, что чем ближе размер заказа к EOQ, тем меньше издержки и наоборот. Следовательно, в тех случаях, когда мы не можем выбрать размер заказа равным EOQ, мы должны взять реально возможную величину заказа, наиболее близкую к экономичному размеру заказа.

В случае с покупкой болтов по цене 5 руб. – это верхняя граница диапазона, т.е. 4999 штук.

Поэтому в таблицу (Рис. 29) кроме строки для расчета EOQ добавлена строка “Реальный Q” – реальный размер заказа. В этой строке мы будем записывать тот размер заказа, который выбираем на самом деле. Конечно, в жизни мы можем выбирать реальный размер заказа, отличный от теоретически оптимального не только из-за диапазонов действия цен. Скажем, во втором столбце, EOQ равен 7563.6 и попадает в диапазон действия цены 4.6 руб. – от 5000 до 19999. Но не можем же мы заказать дробное число болтов. Значит, как минимум надо выбрать реальный размер заказа, как округленное до целых значение EOQ. Кроме того, часто бывает, что штучный товар фасуется в стандартную тару. В этом случае нужно заказывать партию так, чтобы получалось целое число коробок или ящиков и т.п. Могут быть и другие причины, заставляющие отклоняться от теоретической величины оптимального заказа. Поэтому не существует никакой стандартной формулы для реального Q.

В сложных случаях реальный Q можно проставить вручную с учетом известных вам условий. А в нашей задаче можно написать и формулу, так как выбор достаточно прост. Такая формула и записана в ячейке B8.

Формулы для расчета TH, TS и T очевидно нет нужды комментировать. Полная величина издержек включает в себя не только T, но и сумму, истраченную на покупку годового запаса болтов. Годовой запас здесь взят потому, что издержки хранения и заказа тоже вычислены в расчете на год. Все вновь введенные формулы так же, как и формула для EOQ, протягиваются вправо на все шесть ячеек. В результате получаем следующую таблицу (таблица 25).

Таблица 25

В последней строке таблицы выведены наименьшие возможные издержки при покупке болтов по каждой из шести предложенных цен. Из этих шести значений издержек наименьшей оказывается 238 550 руб., которая получается при покупке болтов у поставщика B партиями по 10 тыс. штук по цене 4.5 руб. за штуку.

Из таблицы видно, что покупка болтов по меньшей цене, но более крупными партиями по 20 -30 тыс. штук оказывается чуть дороже, так как предлагаемые скидки полностью съедаются потерями от замораживания капитала при такой политике закупок. 

2.5. Принятие решений в условиях неопределенности и риска

При случайном спросе (даже если он в среднем постоянен) ситуация, очевидно, усложнится. Если спрос за время ожидания поставки новой партии товара случайно оказался выше оставленного запаса, равного ожидаемому среднему спросу d принадлежит L, то возникнет дефицит (кривая уровня запаса во втором цикле уходит в отрицательную область). Если он случайно оказался ниже оставленного запаса d принадлежит L, то в момент прихода на склад новой партии товара, размером EOQ, на складе еще останется некоторое количество этого товара, и уровень запаса будет выше, чем требует модель экономичного размера заказа. Избежать случайных вариаций уровня запаса при случайном спросе, очевидно, нельзя, а вот возникновение дефицита, в рыночных условиях естественно недопустимо. Во-первых, дефицит означает потерю прибыли от упущенных продаж (спрос на которые реально был зафиксирован) и, во-вторых, грозит потерей доброго отношения клиентов, которые, не найдя у вас на складе товар, заявленный в ассортименте, уйдут к вашему конкуренту, что снизит спрос на товары фирмы в будущем.

Вследствие этого правильная оценка риска возникновения дефицита, проведение мероприятий по снижению риска дефицита до приемлемого уровня, обеспечивающего достойный уровень обслуживания клиента, и оценка связанных с ними издержек является важной задачей менеджера, отвечающего за управление запасами.

Если для снижения риска возникновения дефицита создается безопасный резерв, то средний уровень запаса в момент прибытия новой партии товара от поставщика будет равен не нулю, а этому безопасному резерву. Последнее означает повышение среднего уровня запаса на складе на величину безопасного резерва и, соответственно, увеличение издержек хранения по сравнению с их оптимальным значением. Эти дополнительные издержки хранения и есть плата за снижение риска возникновения дефицита:

ΔTH = H * SS

где ΔTH – дополнительные издержки хранения безопасного резерва,

SS – (safety stock) – величина безопасного резерва в единицах хранения (шт.)

H - удельная издержка хранения, представляющая собой процент от стоимости единицы запаса.

Для количественной оценки риска возникновения дефицита при заданном уровне безопасного резерва или, наоборот, для определения величины безопасного резерва при заданном уровне риска возникновения дефицита необходимо знать основные характеристики случайного спроса: его ожидаемое (среднее) значение, стандартное отклонение и частотное распределение (или, точнее, распределение вероятностей) за время поставки.

Важнейшая функция запасов состоит в том, что она играют роль буфера, смягчающего удары, испытываемые фирмой в результате нестабильных поставок сырья или товаров от поставщиков или сильных вариаций потребительского спроса на тот или иной продукт. В производственном процессе, запасы незавершенной продукции (полуфабрикатов) необходимы для обеспечения независимости различных производственных операций.

Однако «молчание больших запасов» не менее опасно, чем «вопли возмущенного клиента». Дело в том, что с запасами связаны специфические издержки хранения, размер которых может составлять 20-40% в год от стоимости среднегодового уровня запаса, при чем, что особенно существенно, большая их часть не проходит через бухгалтерию, как прямые затраты, а является, так называемыми, «упущенными возможностями». Несмотря на то, что их «сразу не видно», большие упущенные возможности, приводят фирму к банкротству так же быстро, как и большие прямые затраты.