Розрахункова робота Побудова виробничої функції та застосування її до дослідження виробничої системи, Варіант №14
Код роботи: 1311
Вид роботи: Розрахункова робота
Предмет: Моделювання економіки
Тема: Побудова виробничої функції та застосування її до дослідження виробничої системи, Варіант №14
Кількість сторінок: 26
Дата виконання: 2016
Мова написання: українська
Ціна: 350 грн (+ Excel-файл)
Вступ
ЗАВДАННЯ 1. ПОБУДОВА ВИРОБНИЧОЇ ФУНКЦІЇ ТА ЗАСТОСУВАННЯ ЇЇ ДО ДОСЛІДЖЕННЯ ВИРОБНИЧОЇ СИСТЕМИ
Хід виконання завдання
ЗАВДАННЯ 2. ЗАСТОСУВАННЯ МОДЕЛІ ЛЕОНТЬЄВА ДО ДОСЛІДЖЕННЯ ЧОТИРИГАЛУЗЕВОЇ ЕКОНОМІЧНОЇ СИСТЕМИ
Хід виконання завдання
ЗАВДАННЯ 3. МОДЕЛЬ ЕКОНОМІЧНОЇ СИСТЕМИ У ВИГЛЯДІ СИСТЕМИ СТРУКТУРНИХ РІВНЯНЬ
Хід виконання завдання
Список використаної літератури
Дана розрахункова робота виконується з дисципліни "Моделювання економіки". Ця дисципліна є одним з головних курсів у процесі підготовки сучасних фахівців з економічної кібернетики. Курс має одночасно теоретичне, методологічне та прикладне значення.
Метою розрахункової роботи є закріплення теоретичних знань про типові економіко-математичні моделі, набуття навичок практичної роботи з ними, програмна реалізація цих моделей. В умовах ринкової економіки використання типових та розробка нових моделей дає змогу правильно оцінити та передбачити різні економічні показники, прийняти оптимальні управлінські рішення. Використання інформаційних технологій на базі комп'ютерів дозволяє автоматизувати певні етапи розробки моделей та дає можливість розв'язувати задачі великих розмірів. В розрахунковій роботі студенти будують економіко-математичні моделі, виконують конкретні розрахунки, які необхідні для дослідження економічних систем.
Для виконання розрахункової роботи необхідні знання з економіки, вищої математики, економетрії, економічної кібернетики та економічної інформатики.
Розрахункова робота передбачає творчий підхід до розв’язання завдань і активне використання програмних засобів MS Excel для автоматизації обчислень.
1. Вітлінський В.В. Моделювання економіки: Навч. посібник. – К.: КНЕУ, 2003.- 408 с.
2. Пономаренко О.І. Пономаренко В.О. Системні методи в економіці, менеджменті та бізнесі.: Навч.посібник. К.-Либідь,1995. - 240 с.
3. Клебанова Т.С., Забродський В.О., Полякова О.Ю., Петренко В.Л. Моделювання економіки: Навч. посібник. – Харків: Видавництво ХДЕУ, 2001.-140 с., рос. мовою.
4. Бережна О.В., Бережной В.Г. Математичні методи моделювання економічних систем. Навч. посібник. – М.: Фінанси та статистика, 2001. – 368 с., рос. мовою.
Завдання 1. Побудова виробничої функції та застосування її до дослідження виробничої системи
На основі статистичних даних, де Х – обсяг випущеної продукції, L – працезатрати, K – основні фонди:
1. Побудуйте економетричну модель виробничої функції Кобба-Дугласа, довівши її адекватність статистичним даним;
2. знайдіть
2.1. середню продуктивність праці та середню продуктивність основних фондів;
2.2. граничну продуктивність праці та граничну ефективність основних фондів;
2.3. коефіцієнт еластичності випуску за працею та коефіцієнт еластичності випуску за основними фондами;
2.4. граничну норму заміщення фондів працею та праці фондами;
3. побудуйте ізокванту у відповідності до варіанту завдання;
4. обґрунтуйте точковий прогноз для заданого значення факторів виробництва.
|
Варіант №14 |
|||
|
№ з/п |
L |
K |
X |
|
1 |
30,1 |
52,1 |
78,2 |
|
2 |
32,6 |
53,5 |
82,5 |
|
3 |
33,7 |
53,1 |
83,8 |
|
4 |
35,1 |
56,5 |
86,7 |
|
5 |
36,4 |
54,1 |
87,0 |
|
6 |
39,4 |
58,2 |
92,8 |
|
7 |
41,8 |
55,1 |
91,5 |
|
8 |
43,3 |
57,2 |
95,3 |
|
9 |
44,2 |
56,1 |
94,7 |
|
10 |
46,0 |
56,1 |
96,7 |
|
11 |
47,8 |
57,1 |
99,5 |
|
12 |
49,5 |
58,7 |
102,9 |
|
Прогноз |
49,7 |
58,1 |
|
|
Ізокванта |
|
|
91,5 |
Завдання 2. Застосування моделі Леонтьєва до дослідження чотиригалузевої економічної системи
Економічна система складається з чотирьох галузей. Задана матриця А коефіцієнтів прямих матеріальних витрат та заданий бажаний вектор випуску кінцевої продукції Y.
1. Перевірити, чи здатна економічна система забезпечити невід’ємний кінцевий випуск.
2. Побудувати модель Леонтьєва («витрати-випуск») та знайти вектор валової продукції X.
3. Побудувати міжгалузеву балансову модель виробництва і розподілу продукції.
4. Побудувати міжгалузеву балансову модель витрат праці. Використати таку кількість трудових ресурсів: Т=(120i ; 200i ;180і ; 250і), де і – номер варіанту.
Всі розрахунки виконувати із застосуванням матричних функцій Excel: MУМНОЖ(…)- множення матриць, МОБР(…) – знаходження оберненої до заданої матриці. Проілюструвати виконання роботи скриншотами.
Варіант 14.
Для чотиригалузевої економічної системи задані матриця коефіцієнтів прямих матеріальних витрат А і вектор кінцевої продукції Y:
,
|
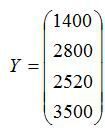ВАРІАНТ №14 |
|
|||
|
А= |
0,09 |
0,23 |
0,41 |
0,26 |
|
0,25 |
0,26 |
0,21 |
0,18 |
|
|
0,09 |
0,24 |
0,2 |
0,11 |
|
|
0,2 |
0,21 |
0,17 |
0,11 |
|
Завдання 3. Модель економічної системи у вигляді системи структурних рівнянь
За заданими вихідними даними (див. табл.1 та табл.2) для заданої моделі економічної системи (див. варіанти завдань):
1) виділити ендогенні та екзогенні змінні;
2) записати приведену форму моделі;
3) визначити коефіцієнти приведеної форми моделі;
4) обчислити значення інструментальних змінних;
5) визначити коефіцієнти структурної моделі;
6) перевірити значущість отриманих рівнянь та їх коефіцієнтів;
7) перевірити економетричні моделі на адекватність;
8) записати модель економічної системи.
Отримана модель має бути адекватною з ймовірністю 0,95.
ВАРІАНТ 14
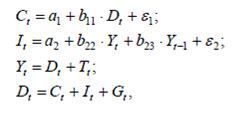(1),
де C – витрати на споживання; Y– чистий національний продукт; I – інвестиції; T- податки; G – державні витрати; D – чистий національний дохід;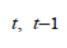 
- поточний і попередній періоди; 
, 
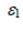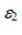- випадкові похибки.
Таблиця 3.1
|
Поточний період t |
Витрати на особисте споживання С* (млрд. грн.) |
Внутр. інвестиції І (млрд. грн.)
|
Чистий національний продукт Y (млрд. грн.) |
Чистий національний дохід D (млрд. грн.)
|
Податки
T (млрд. грн.)
|
Державні витрати G (млрд. грн.)
|
|
1 |
872,0 |
267,0 |
1412,7 |
1108,4 |
364,3 |
486,1 |
|
2 |
1313.0 |
376,0 |
1978,9 |
1468,8 |
473,0 |
652,7 |
|
3 |
1597,0 |
408,8 |
2229,0 |
1626,5 |
594,1 |
839,0 |
|
4 |
1811,0 |
407,1 |
2514,4 |
1706,6 |
564,6 |
842,1 |
|
5 |
2870,0 |
670,4 |
4632,0 |
3359,9 |
1007,6 |
1258,0 |
|
6 |
3813,0 |
1165,2 |
7116,6 |
5174,1 |
1707,6 |
1960,1 |
|
7 |
5014,0 |
1504,7 |
8819,9 |
6329,7 |
2345,0 |
2419,4 |
|
8 |
6390,0 |
1762,4 |
10627,5 |
7294,8 |
3137 |
3422,3 |
|
9 |
7710,0 |
2186,4 |
12886,1 |
8755,2 |
3735,0 |
3964,9 |
|
10 |
9814,0 |
2865,0 |
16679,9 |
11994,0 |
4942,0 |
4669,7 |
|
11 |
12391,0 |
3611,1 |
21079,5 |
15609,0 |
5949,0 |
6820,6 |
|
12 |
15147,0 |
4730,0 |
26078,0 |
19258,0 |
7162,0 |
8375,2 |
|
13 |
18644,0 |
6627,0 |
32213,0 |
24400,0 |
9469,0 |
11377,0 |
|
14 |
27423,0 |
8782,0 |
40222,0 |
24710,0 |
12008,0 |
13992,0 |
|
15 |
29191,0 |
7930,0 |
37862,0 |
22493,0 |
10430,0 |
16048,0 |