« Назад

Мета: Вивчення арифметичних операцій і порівнянь.

Хід роботи

Арифметичні вирази складаються з операндів (чисел і змінних), операторів (+, -, *, /, div и mod) і дужок. Символи в правій частині від знака рівності (який є предикатом =) складають арифметичний вираз, наприклад:

А = 1 + 6 / (11 + 3) * Z

Шістнадцяткові і восьмирічні числа починаються з "0х" або "0о"

відповідно, наприклад:

0xFFF =4095

86 = 0о112+12

Значення виразу може бути обчислено, тільки якщо всі змінні в момент обчислення визначені. При цьому обчислення проводяться в порядку, що визначається пріоритетом операції. Операції з вищим пріоритетом виконуються першими.

Операції

Visual Prolog може виконувати всі чотири основні арифметичні операції (додавання, віднімання, множення і ділення) між цілими і дійсними числами. Тип результату наведено в таблиці 1.

Таблиця 1

Арифметичні операції

Операнд 1	Оператор	Операнд 2	Результат
Ціле	+, -, *	Ціле	Ціле
Дійсне	+, -, *	Ціле	Дійсне
Ціле	+, -, *	Дійсне	Дійсне
Дійсне	+, -, *	Дійсне	Дійсне
Ціле або дійсне	/	Ціле або дійсне	Дійсне
Ціле	Div	Ціле	Ціле
Ціле	Mod	Ціле	Ціле

У разі змішаної цілочисельної арифметики, що включає і знакові і беззнакові числа, результат знаковий. Розмір результату буде дорівнювати більшому із розмірів двох операндів.

Порядок обчислень

Арифметичні операції обчислюються в такому порядку:

- Якщо вираз містить підвираз в дужках, підвираз обчислюється першим;

- Якщо вираз містить операції множення (*) або ділення (/, div або mod), ці операції виконуються зліва направо;

- Якщо вираз містить операції додавання (+) і віднімання (-), вони виконуються також зліва направо.

Порядок операцій показано у таблиці 2.

Таблиця 2

Порядок операцій

Операція	Пріоритет
+, -	1
*, /, mod, div	2
-, + (унарні)	3

У виразі А = 1 + 6 / ( 11 + 3 ) * z , припустимо, що z має значення 4 , бо змінні повинні бути зв'язані до обчислення. Обчислимо цей вираз:

1. (11 + 3) – перший обчислюваний підвираз, так як він взятий у дужки, він обчислюється як 14.

2. Потім обчислюється 6/14, так як / і * обчислюються зліва направо. В результаті отримаємо 0.428571.

3. Потім 0.428571*4 дає 1.714285.

4. Обчислюючи 1 + 1.714285, отримуємо значення виразу 2.714285. Одержане значення 2.714285 належить дійсному домену.

Функції і предикати

Visual Prolog має повний набір вбудованих математичних функцій і предикатів, які використовують цілі і дійсні значення.

При використанні математичних функцій і предикатів (крім div, mod) необхідно підключити бібліотеку math і перед викликом самої функції також прописати math (наприклад, Y=math::cos(X)). Повний їх список наведено в таблиці 3.

Таблиця 3

Арифметичні предикати і функції Visual Prolog

Ім’я	Опис
X mod Y	Повертає залишок від ділення (модуль) X на Y
X div Y	Повертає частку від ділення х на Y
abs (X)	Якщо    значення   X   -   позитивна   величина   value,   abs(X)
	повертає це значення, інакше - 1 * value
cos(X)	Повертає косинус свого аргументу
sin(X)	Повертає синус свого аргументу
tan(X)	Повертає тангенс свого аргументу
arctan(X)	Повертає арктангенс дійсного значення, з яким зв'язаний X
exp(X)	Підносить е в ступінь X
ln(X)	Логарифм X з основою е
log(X)	Логарифм X з основою 10
sqrt (X)	Корінь квадратний з X
random (X)	Присвоює X випадкове дійсне число; 0<=X<1
random(X, Y)	Присвоює Y випадкове ціле число; 0<=Y<X
round (X)	Округлює значення X, результат дійсний
trunc(X)	Усікає X, результат дійсний

Тригонометричні функції вимагають, щоб X був величиною, що представляє кут в радіанах.

Генератор випадкових чисел

Для генерації випадкових чисел в Visual Prolog передбачені два стандартних предиката. Один з них повертає випадкове дійсне число в діапазоні від 0 до 1, другий повертає випадкове ціле число в діапазоні від 0 до даного числа. Крім того, випадкова числова послідовність може бути переініціалізована.

При використанні генератора випадкових чисел необхідно підключити бібліотеку math і перед викликом самих предикатів також прописати math (наприклад, Y=math::random()).

Предикат random/1

Ця версія random повертає випадкове дійсне число RandomReal, яке задовольняє умові:

Предикат random/2

Ця версія random має два аргументи, його формат:

random(MaxValue, Randomlnt) %(i,о)

Цей предикат ставить у відповідність Randomlnt випадкове ціле, що задовольняє умові:

0 <= Randomlnt < MaxValue

Предикат random/2 працює значно швидше, ніж random/1, так як random/2 використовує тільки цілочисельну арифметику.

Предикат randomInit/1

randomInit ініціалізує генератор випадкових чисел і має формат:

randomInit(Seed) %(i)

За замовчуванням випадкове початкове значення генерується як функція системного часу, і аргумент seed предиката randomInit встановлює початкове значення. Основне призначення randomInit - надати повторювану послідовність псевдовипадкових чисел для статистичного тестування.

Обидві – цілочисельна і дійсна - версії random використовують однакове початкове значення і базовий генератор чисел.

Приклад 1. Використання генератора випадкових чисел

Як приклад наведемо програму, яка використовує random/1 для вибору заданої кількості імен з п'яти випадковим чином.

Лістинг програми

Для кнопки OK необхідно прописати наступний код:

 

Рис. 1. Форма для вводу кількості імен із програми із прикладу 1

Рис. 2. Результат виконання програми з прикладу 1

Цілочисельна і дійсна арифметика

Visual Prolog підтримує предикати і функції модульної арифметики, цілого ділення, квадратні корені і абсолютні значення, тригонометричні і трансцендентні функції, округлення (вгору або вниз) і усічення. Вони наводяться в таблиці 3.

Функція mod/2

Функція mod обчислює залишок від ділення X на Y (де X і Y — цілі).

X mod Y %(i,i)

Вираз Z = X mod Y ставить у відповідність Z результат — залишок від ділення X на Y.

Наприклад:

Z = 7 mod 4 % Z буде дорівнювати 3

Y = 4 mod 7 % Y буде дорівнювати 4

Функція div/2

Функція div обчислює цілу частку від ділення X на Y (де X і Y — цілі).

X div Y %(i,i)

Вираз Z = X div Y ставить у відповідність Z цілу частину результату. Наприклад:

Z = 7 div 4 % Z буде дорівнювати 1

Y = 4 div 7 % Y буде дорівнювати 0

Функція abs/1

Функція abs повертає абсолютне значення свого аргументу.

math::abs(X) %(i)

Вираз Z = math::abs(X) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже визначено. Наприклад:

Z = math::abs(-7) % Z буде дорівнювати 7

Функція cos/1

Функція cos повертає значення косинуса свого аргументу.

math::cos(X) %(i)

Вираз Z = math::cos (X) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже визначено. Наприклад:

Pi = 3.141592653,

Z = math::cos(Pi) % Z буде дорівнювати -1

Функція sin/1

Функція sin повертає значення синуса свого аргументу.

math::sin(X) %(i)

Вираз Z = math::sin(X) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже визначено. Наприклад:

Pi = 3.141592653,

Z = math::sin(Pi) % Z буде майже дорівнювати 0

Функція tan/1

Функція tan повертає значення тангенса свого аргументу.

math::tan(X) %(i)

Вираз Z = math::tan(X) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже визначено. Наприклад:

Pi = 3.141592653,

Z = math::tan(Pi) % Z буде дорівнювати майже 0

Функція arctan/1

Функція arctan повертає значення арктангенса від дійсного значення, з яким зв’язаний X.

math::arctan(X) % (i)

Вираз Z = math:: arctan (X) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже визначено. Наприклад:

Pi = 3.141592653,

Z = math::arctan(Pi)    % Z буде дорівнювати 1.2626272556

Функція ехр/1

Функція ехр повертає значення е у степені значення, з яким зв’язаний X. math::ехр(Х) %(i)

Вираз Z = math::ехр(Х) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже визначено. Наприклад:

Z = math::ехр(2.5) % Z буде дорівнювати 12.182493961

Функція ln/1

Функція ln повертає значення натурального логарифма з X (з основою е).

math::ln(X) %(i)

Вираз Z = math::ln(X) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже визначено. Наприклад:

Z = math::ln(12.182493961) % Z буде дорівнювати 2.5

Функція log/1

Функція log повертає значення логарифма з основою 10 з X. math::log(X) % (i)

Вираз Z = math::log(X) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже визначено. Наприклад:

Z = math::log(2.5) % Z буде дорівнювати 0.39794000867

Функція sqrt/1

sqrt повертає квадратний корінь з X. math::sqrt(X) %(i)

Вираз                       Z = math:: sqrt (X) ставить у відповідність Z (якщо воно вільне) результат, або поверне успіх / неуспіх, якщо Z вже зв’язане. Наприклад:

Z = math::sqrt(25) %Z буде дорівнювати 5

Функція round/1

round повертає округлене значення X.

math::round(X) %(i)

Функція round округлює X до найближчого цілого, але не виконує перетворення типу. Наприклад:

Zl = math::round(4.51) % Zl буде дорівнювати 5.0

Z2 = math::round(3.40) % Z2 буде дорівнювати 3.0

Обидва Z1 і Z2 — дійсні значення, як показано вище; тільки дробові частини аргументів round округлюються до найближчого цілого.

Функція trunc/1

Функція trunc усікає X зправа до десяткового дробу, відкидаючи дробову частину. Як і round, trunc не   виконує перетворення типів:

math::trunc(X)    %     (i) .

Наприклад:

Z = math::trunc(4.7)    % Z буде дорівнювати 4.0, Z — дійсне число.

Порівняння

Visual Prolog може порівнювати арифметичні вирази так само, як символи, рядки і ідентифікатори. Наступний вираз в Visual Prolog еквівалентний виразу: "Сума X плюс 4 менше 9 мінус Y".

X+ 4 < 9 -Y

Оператор відношення "менше ніж" (<) показує відношення між двома виразами: X + 4 і 9 - Y.

Visual Prolog використовує інфіксну нотацію, яка означає, що оператор розташовується між операндами (X+4) замість того, щоб передувати їм (+(X,4)).

Повний ряд відношень, дозволених в Visual Prolog, наведено в таблиці 4.

Оператори відношення

Таблиця 4

Ідентифікатор	Відношення	Ідентифікатор	Відношення
<  <= =	Менше Менше або дорівнює Дорівнює	>  >= <> або ><	Більше Більше або дорівнює Не дорівнює

Рівність і предикат рівності

В Visual Prolog такі оператори, як N = N1 - 2 показують відношення між трьома об'єктами (N, N1 і 2) або відношення між двома об'єктами (N і величиною N1 - 2). Якщо N ще вільне, оператор може бути задоволений присвоєнням n значення виразу N1 - 2. Це приблизно відповідає тому, що в інших мовах програмування називається оператором присвоювання. Зауважимо, що оскільки N1 є частиною обчислюваного виразу, воно завжди має бути визначено (тобто має бути зв'язане зі значенням).

Коли ви для порівняння дійсних величин використовуєте предикат рівності (=), потрібно подбати про те, щоб наближене представлення дійсних чисел не привело до непередбачуваних результатів.

Наприклад, ціль 7 / 3 * 3 = 7 зазнає невдачі (точний результат залежить від точності обчислення чисел з плаваючою крапкою, що використовується на вашій платформі).

Приклад 2. Використання предиката рівності

Наступна програма перевіряє, чи рівні два числа. Якщо числа не рівні, то знаходить різницю.

Лістинг програми

Для кнопки OK необхідно прописати наступний код.

Рис. 3. Форма для вводу двох чисел для порівняння з програми з прикладу 2

Рис. 4. Результат виконання програми з прикладу 2

Приклад 3. Рішення квадратного рівняння

Наступна програма показує, як обробити приблизну рівність. Вона являє собою ітеративну процедуру обчислення квадратного кореня для визначення рішень квадратного рівняння: А*Х*Х + В*Х + С = 0.

Наявність рішень залежить від значення дискримінанта D, що визначається як

D = В*В - 4*А*С

У даному випадку:

1. D > 0 — означає, що існує два різних рішення.

2. D = 0 — означає, що існує єдине рішення.

3. D < 0 — означає, що рішень немає, якщо X - дійсне (можуть бути одне або два комплексних рішення).

Лістинг програми

Для кнопки OK необхідно прописати наступний код.

Рис.5. Форма для вводу коефіцієнтів квадратного рівняння з програми із прикладу 3

Рис. 6. Результат виконання програми із прикладу 3

Щоб вирішити квадратне рівняння, ця програма обчислює квадратний корінь з дискримінанта D. Програма обчислює квадратні корені за ітеративною формулою, де нове значення (NewGuess) квадратного кореня з X може бути отримане з попереднього значення (Guess): NewGuess = Guess- (Guess*Guess-X)/2/Guess

Кожна ітерація трохи наближається до квадратного кореня з X. коли умова equal (X, Y) задовольняється, подальшого наближення досягти не можна - обчислення закінчується. Тепер програма може розв’язати квадратне рівняння, використовуючи значення X1 и Х2

X1 = (-В + sqrtD)/(2*A) Х2 = (-В - sqrtD)/(2*A)

Порівняння символів, рядків

Крім числових виразів ви можете також порівнювати прості символи, рядки і ідентифікатори. Розглянемо наступні порівняння:

Символи

Використовуючи відповідне значення коду ASCII для кожного символу, Visual Prolog перетворює 'а'<'b' в еквівалентний арифметичний вираз 97 <98.

Відзначимо, що надійними є тільки 7-бітові ASCII порівняння (тобто букви верхнього і нижнього регістрів a - z, цифри і т. д.). 8-бітові символи, що використовуються для деяких національних символів, не завжди виявляються переносними між різними платформами.

Рядки

Коли рядки або ідентифікатори порівнюються, результат залежить від порівняння символів на відповідних позиціях. Результат дорівнює тому, який ви отримали б при порівнянні перших символів в тому випадку, якщо ці два символи не рівні. Якщо ж вони рівні, Visual Prolog порівнює наступну відповідну пару символів і повертає результат у тому випадку , якщо цього разу вони не рівні. В іншому випадку перевіряється третя пара і т. д.

Порівняння закінчується, коли або знайдені два різних символи, або досягнуто кінець кожного з рядків. Якщо кінець досягнуто, і пару різних символів не знайдено, більш короткий рядок вважається меншим.

Порівняння "antony" > "antonia" оцінюється як true (істина), так як перша пара різних символів містить у першому рядку букву y (значення 79 в коді ASCII), а в іншому рядку букву i (ASCII значення 69). Аналогічно, порівняння "аа" > "а" істина.

Вираз "peter" > "sally" буде хибним, так як визначається порівнянням значень ASCII перших літер слів peter і sally. Символ p розташовується перед символом s в алфавіті, тому p має менше значення коду ASCII. Таким чином, вираз буде оцінено як помилковий.

Завдання

Написати додаток на основі форми, що обчислює значення функції при різних умовах.

Варіанти завдань:

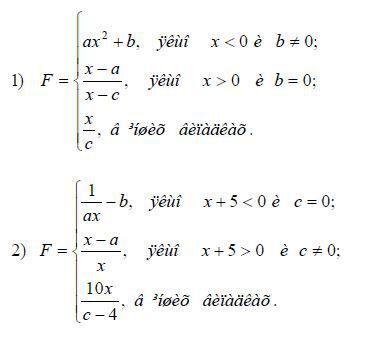
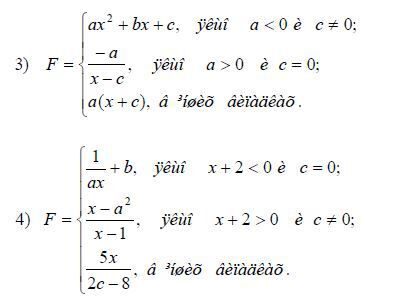
Контрольні питання

1. У якому випадку значення змінної може бути не обчислено?

2. Назвіть порядок виконання арифметичних операцій в Visual Prolog?

3. Якою розмірністю повинна бути змінна для використання тригонометричних функцій?

4. Для чого потрібні предикати random/1 і random/2, і в чому їх відмінність?

5. Особливості предиката randomInit/1.