Лекція Формалізація поведінки системи

« Назад

1. Поняття перетворення та його опис

Виникає запитання: чи у кожній системі можна реалізувати управління?

Виявляється, не у кожній. Для існування управління в системі потрібне виконання певних умов щодо СУ та ОУ, а саме:

1) Об’єкт управління повинен мати здатність переходити до різних станів. Такий перехід можна розуміти не тільки як переміщення у фізичному просторі, зміну швидкості або напряму (траєкторії) руху, а й як зміну будь-яких властивостей.

Практично завжди можна виокремити деякі параметри, кількісні значення яких характеризують стан системи в кожний момент часу. Для фізичного об’єкта це маса, геометричні розміри, температура, швидкість, колір; для підприємства — кількість працюючих, випуск продукції за кожним із найменувань, собівартість, прибуток та інші показники; для економіки як системи — це ВВП, стан платіжного та торговельного балансу, рівень інфляції та безробіття, валютний курс, процентні ставки тощо.

У кожному конкретному випадку, отримавши перелік параметрів, які в деякому сенсі повно характеризують ОУ, ми визначаємо багатовимірний простір станів, в яких може перебувати система.

Будь-який стан системи характеризується набором кількісних значень кожного із зазначених параметрів і у просторі станів відображується деякою так званою відображувальною точкою. Змінам станів системи відповідає переміщення відображувальної точки у просторі станів. Задавши межі можливих значень кожного з незалежних параметрів системи, визначають область простору станів, в якій може перебувати відображувальна точка області допустимих станів.

Простір станів може бути неперервним (температура, швидкість і т. ін.) або дискретним (кількість робітників, валютний курс тощо).

Кількість вимірів простору станів дорівнює кількості незалежних параметрів, що визначають стан системи.

Управління полягає в такому впливі на ОУ, щоб він переходив з одного стану до іншого.

При цьому відображувальна точка рухається в області допустимих станів.

Якщо стан системи жорстко зафіксований, то поняття управління втрачає сенс.

2) Система управління має бути реально здатною змінювати стан об’єкта управління відповідно до прийнятих рішень. У загальному випадку рішення видаються у вигляді керуючих впливів, що надходять до виконавчих органів, які й змінюють стан керованої системи.

Коли рішення, що їх приймає система управління, дуже мало впливають на зміну стану об’єкта управління, то управління фактично не відбувається.

3) Будь-яке управління має бути низкою цілеспрямованих (невипадкових), пов’язаних між собою керуючих впливів. Це означає, що має бути відома мета управління, тобто деякий кінцевий стан системи, що характеризується певним набором кількісних значень параметрів, які потрібно забезпечити на стадії розгляду управління. У просторі станів мета подається точкою, куди має бути переведено систему з того стану, в якому вона перебуває в даний момент. Якщо мета управління невідома, управління системою не має сенсу.

Рух системи, що не має кінцевої мети, перетворюється на безладне блукання.

4) Система управління повинна мати змогу вибирати рішення з деякого набору можливих рішень. В умовах жорстких обмежень найбільш ефективні рішення часто залишаються за межами допустимої області.

Якщо система управління має лише єдине можливе рішення, тобто позбавлена можливості вибору, то вона фактично не здійснює управління.

5) Система управління повинна мати у своєму розпорядженні матеріальні, фінансові, трудові, інформаційні та інші ресурси, що забезпечують реалізацію вибраних керуючих впливів. За відсутності таких ресурсів вона позбавлена свободи вибору. Управління без ресурсів, що забезпечують реалізацію керуючих впливів, неможливе.

6) Для правильного вибору характеру і міри керуючих впливів Система управління повинна знати не тільки мету та кінцевий стан, якого потрібно досягти, а й поточний стан Об’єкта управління, в якому він перебуває в даний момент. Тільки тоді Система управління може вибрати правильний шлях або траєкторію руху системи та прийняти рішення, що спрямовують цим шляхом.

За відсутності інформації про стан керованої системи процес управління стає неможливим або, щонайменше, неефективним.

7) Об’єкт управління перебуває під впливом не лише системи управління, а й зовнішнього середовища, на яке Об’єкт управління і сам певною мірою впливає. Через наявність взаємозв’язків між всіма об’єктами, явищами й процесами у природі «рух» Об’єкта управління (або відповідної точки в просторі станів) відбувається під впливом як керуючих впливів системи управління, так і зовнішнього середовища. Ці впливи можуть відхиляти рух системи від обраної траєкторії.

Природно, що чим докладніше вивчено реакцію системи на зовнішні впливи і чим повнішою є інформація про самі зовнішні впливи, тим ефективнішими можуть бути вибрані керуючі впливи.

Якщо поведінку системи розглядати як ланцюг послідовних скінчених змін її станів, то змінні (параметри) системи, змінюючись у часі, в кожний даний момент характеризуватимуться деякими значеннями.

Якщо одне певне значення змінної u₁ у момент часу t₁ перетворюється на наступне значення u₂ у момент t₂, то вважається що відбувся перехід з (u₁,t₁) в (u₂,t₂).

Чинник, під дією якого відбувається перехід, називається оператором. Змінна, на яку чинить дію оператор, називається операндом.

Результат переходу - (u₂,t₂) - називається образом.

Якщо розглядати деяку множину всіх переходів системи із стану а в стан в, із стану с в стан d і т. д., то така множина переходів для деякої множини операндів називається перетворенням.

 

2. Метод У. Ешбі інтерпретації перетворень

Перетворенням можна дати математичне уявлення за допомогою методу, запропонованого У. Р. Ешбі.

Нехай деяка множина станів системи включає стани а, b, с, d і на цю множину операндів діє оператор Р, тоді поведінку системи можна описати таким чином:

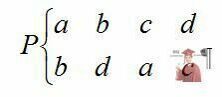
У першому рядку запису перераховані стани системи, або операнди. В другому рядку, під кожним операндом, знаходяться образи, в які система переходить із станів, записаних у верхньому рядку, під дією оператора Р. В цьому перетворенні множина образів другого рядка не містить жодного нового елементу. Перетворення, яке не породжує нових елементів, називається замкнутим.

Розглянемо ще один приклад перетворення:

.

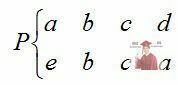У цьому перетворенні множина образів містить новий елемент е; перетворення виходить за межі системи, і тому називається незамкнутим.

Перетворення 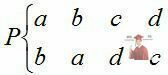 є однозначним, взаємно однозначним, замкнутим.

Наведемо приклад неоднозначного перетворення:

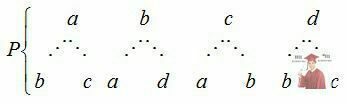
Перетворення вигляду 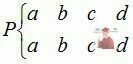 є тотожним.

Можна використовувати компактніші форми запису. Наприклад, якщо операнди - суть ДОДАТНІ числа 1, 2, 3, 4, і діє оператор "додати до кожного числа 3", то перетворення можна записати:

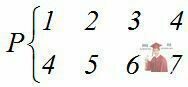, або в компактній формі:   (n=1,2,3,4).

 

3. Типи поведінки системи

Розрізняють три типи, або режими поведінки системи: рівноважний, перехідний і періодичний.

Стан рівноваги системи може розглядатися як деяка тотожність перетворень, що відбуваються в ній, які визначають однаковий стан системи на будь-якому кроці її розвитку.

 В рівноважному стані системі кожна частина знаходиться в стані рівноваги в умовах, визначуваних іншими її частинами.

Важливим поняттям є поняття циклу в перетворенні системи.

Циклом називається така послідовність станів системи, при якій повторна зміна перетворень примушує відображувальну точку, пробігати повторно цю послідовність.

Цикл можна проілюструвати таким перетворенням:

.

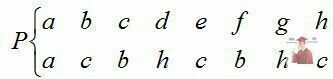Починаючи з а, одержимо послідовність: 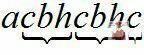  описує цикл.

Якщо в системі перетворення має вигляд:

,

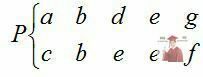то у випадках станів b і е система знаходилася в стані рівноваги.

Якщо Р має вигляд: ,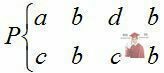

період  є перехідним періодом в поведінці системи.

Перетворення Р вигляду 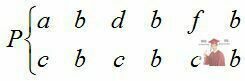ілюструє випадок періодичного рівноважного режиму поведінки системи.

 

4. Рівновага та стійкість системи

Стан стійкості не тотожній стану рівноваги. Під стійкістю системи розуміється збереження нею стану незалежно від зовнішніх збурюючих впливів. Характеристика системи як стійкої не завжди визначає позитивну сторону з погляду управління: система не здатна гнучко реагувати на управління.

Трактування поняття стійкості дозволяє визначити характеристику інваріантності. Інваріантність в послідовності станів системи полягає в тому, що, не зважаючи на зміни, що зазнає система в цілому, деякі її властивості залишаються незмінними.

Використання комплексу ідей, пов'язаних з поняттям стійкості, рівноваги в поведінці систем, вельми корисно при вивченні економічних систем, перш за все, при аналізі виробничих систем.

Перш за все, стан системи вивчається з позицій можливої його рівноваги, тобто чи змінюється він, будучи підданим яким-небудь перетворенням. Розглядається, чи є ця рівновага достатньо стійкою, і якщо так, то який режим поведінки системи, що вивчається.

Якщо є рівноважний стан (або стани) і конкретні збурення, то аналізується, чи повернеться система після відхилення в свою початкову область станів. І якщо система неперервна, то розглядається, чи є вона стійкою проти всіх збурень всередині певній області значень. Даний метод розгляду стану і поведінки системи дає можливість вирішувати питання аналізу економічних систем і забезпечити передумови їх функціонування в оптимальному з позицій деяких вимог режимі.